纯python3和numpy实现的符号计算深度学习框架 .rar

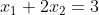
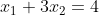
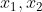## 代码示例 * [递归下降解线性方程组](#递归下降解线性方程组) * [线性回归](#线性回归) * [线性SVM](#线性SVM) * [2x4x2神经网络环状数据分类](#2x4x2神经网络环状数据分类) * [2x8x8x2神经网络螺旋型数据分类](#2x8x8x2神经网络螺旋型数据分类) * [2x16x16x16x3网络实现多分类](#2x16x16x16x3网络实现多分类) * [2x8x8x8x8x2网络分类网格状数据](#2x8x8x8x8x2网络分类网格状数据) * [回归神经网络](#回归神经网络) * [卷积神经网络](#卷积神经网络) ### 递归下降解线性方程组   初始化为 0, 0 ```python import paradox as pd # 定义符号，A为方程系数矩阵，x为自变量，b为常数项。 A = pd.Constant([[1, 2], [1, 3]], name='A') x = pd.Variable([0, 0], name='x') b = pd.Constant([3, 4], name='b') # 使用最小二乘误差定义loss。 loss = pd.reduce_mean((A @ x - b) ** 2) # 创建梯度下降optimizer optimizer = pd.GradientDescentOptimizer(0.01) # 创建loss的计算引擎，申明变量为x。 loss_engine = pd.Engine(loss, x) # 迭代至多10000次最小化loss。 for epoch in range(10000): optimizer.minimize(loss_engine) loss_value = loss_engine.value() print('loss = {:.8f}'.format(loss_value)) if loss_value < 0.0000001: # loss阈值。 break # 输出最终结果。 print('\nx =\n{}'.format(x.value)) ``` 运行结果： ``` ... loss = 0.00000010 loss = 0.00000010 loss = 0.00000010 x = [ 0.99886023 1.00044064] ``` [回到顶部](#readme) ### 线性回归 ```python import numpy as np import matplotlib.pyplot as plt import paradox as pd # 随机生成点的个数。 points_sum = 200 x_data = [] y_data = [] # 生成y = 2 * x + 1直线附近的随机点。 for _ in range(points_sum): x = np.random.normal(0, 2) y = x * 2 + 1 + np.random.normal(0, 2) x_data.append(x) y_data.append(y) x_np = np.array(x_data) y_np = np.array(y_data) # 定义符号。 X = pd.Constant(x_np, name='x') Y = pd.Constant(y_np, name='y') w = pd.Variable(0, name='w') b = pd.Variable(1, name='b') # 使用最小二乘误差。 loss = pd.reduce_mean((w * X + b - Y) ** 2) # 创建loss计算引擎，申明变量为w和b。 loss_engine = pd.Engine(loss, [w, b]) # 梯度下降optimizer。 optimizer = pd.GradientDescentOptimizer(0.00005) # 迭代100次最小化loss。 for epoch in range(100): optimizer.minimize(loss_engine) loss_value = loss_engine.value() print('loss = {:.8f}'.format(loss_value)) # 获取w和b的训练值。 w_value = pd.Engine(w).value() b_value = pd.Engine(b).value() # 绘制图像。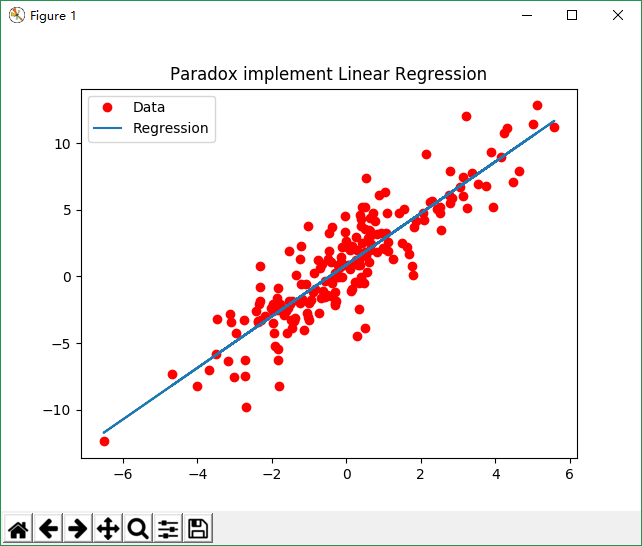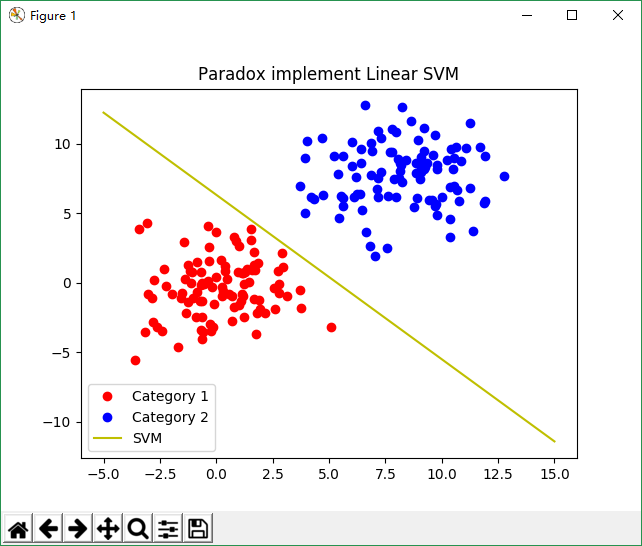 plt.title('Paradox implement Linear Regression') plt.plot(x_data, y_data, 'ro', label='Data') plt.plot(x_data, w_value * x_data + b_value, label='Regression') plt.legend() plt.show() ``` 运行结果：  [回到顶部](#readme) ### 线性SVM ```python import numpy as np import matplotlib.pyplot as plt import paradox as pd # 每类随机生成点的个数。 points_sum = 100 c1_x = [] c1_y = [] c2_x = [] c2_y = [] # 分别在(0, 0)点附近和(8, 8)点附近生成2类随机数据。 for _ in range(points_sum): c1_x.append(np.random.normal(0, 2)) c1_y.append(np.random.normal(0, 2)) c2_x.append(np.random.normal(8, 2)) c2_y.append(np.random.normal(8, 2)) # 定义符号。 c1 = pd.Constant([c1_x, c1_y], name='c1') c2 = pd.Constant([c2_x, c2_y], name='c2') W = pd.Variable([[1, 1], [1, 1]], name='w') B = pd.Variable([[1], [1]], name='b') # 定义SVM loss函数。 loss = pd.reduce_mean(pd.maximum(0, [[1, -1]] @ (W @ c1 + B) + 1) + pd.maximum(0, [[-1, 1]] @ (W @ c2 + B) + 1)) # 创建loss计算引擎，申明变量为W和B。 loss_engine = pd.Engine(loss, [W, B]) # 创建梯度下降optimizer。 optimizer = pd.GradientDescentOptimizer(0.01) # 迭代至多1000次最小化loss。 for epoch in range(1000): optimizer.minimize(loss_engine) loss_value = loss_engine.value() print('loss = {:.8f}'.format(loss_value)) if loss_value < 0.001: # loss阈值。 break # 获取W和B的训练结果。 w_data = pd.Engine(W).value() b_data = pd.Engine(B).value() # 计算分类直线的斜率和截距。 k = (w_data[1, 0] - w_data[0, 0]) / (w_data[0, 1] - w_data[1, 1]) b = (b_data[1, 0] - b_data[0, 0]) / (w_data[0, 1] - w_data[1, 1]) # 分类面的端点。 x_range = np.array([np.min(c1_x), np.max(c2_x)]) # 绘制图像。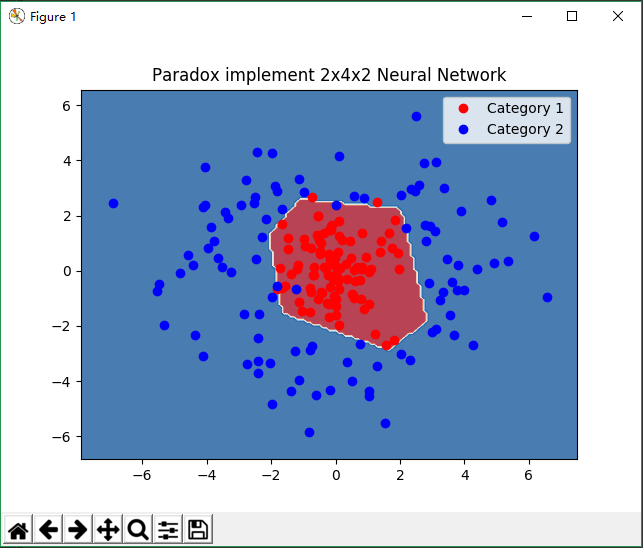 plt.title('Paradox implement Linear SVM') plt.plot(c1_x, c1_y, 'ro', label='Category 1') plt.plot(c2_x, c2_y, 'bo', label='Category 2') plt.plot(x_range, k * x_range + b, 'y', label='SVM') plt.legend() plt.show() ``` 运行结果：  [回到顶部](#readme) ### 2x4x2神经网络环状数据分类 ```python import numpy as np import matplotlib.pyplot as plt import paradox as pd # 每类随机生成点的个数。 points_sum = 100 # 在(0, 0)点附近生成一堆点然后以4为半径在周围生成一堆点构成2类随机数据。 c1_x, c1_y, c2_x, c2_y = [], [], [], [] for _ in range(points_sum): c1_x.append(np.random.normal(0, 1)) c1_y.append(np.random.normal(0, 1)) r = np.random.normal(4, 1) theta = np.random.normal(0, 2 * np.pi) c2_x.append(r * np.cos(theta)) c2_y.append(r * np.sin(theta)) c_x = c1_x + c2_x c_y = c1_y + c2_y # 定义符号。 A = pd.Variable([c_x, c_y], name='A') W1 = pd.Variable(np.random.random((4, 2)), name='W1') # 输入层到隐含层的权重矩阵。 W2 = pd.Variable(np.random.random((2, 4)), name='W2') # 隐含层到输出层的权重矩阵。 B1 = pd.Variable(np.random.random((4, 1)), name='B1') # 隐含层的偏置。 B2 = pd.Variable(np.random.random((2, 1)), name='B2') # 输出层的偏置。 K = pd.Constant([[-1] * points_sum + [1] * points_sum, [1] * points_sum + [-1] * points_sum]) # 构建2x4x2网络，使用ReLu激活函数。 model = pd.maximum(W2 @ pd.maximum(W1 @ A + B1, 0) + B2, 0) # 使用SVM loss。 loss = pd.reduce_mean(pd.maximum(pd.reduce_sum(K * model, axis=0) + 1, 0)) # 创建loss计算引擎，申明变量为W1，W2，B1和B2。 loss_engine = pd.Engine(loss, [W1, W2, B1, B2]) # 创建梯度下降optimizer。 optimizer = pd.GradientDescentOptimizer(0.03) # 迭代至多10000次最小化loss。 for epoch in range(10000): optimizer.minimize(loss_engine) if epoch % 100 == 0: # 每100次epoch检查一次loss。 loss_value = loss_engine.value() print('loss = {:.8f}'.format(loss_value)) if loss_value < 0.001: # loss阈值。 break # 创建预测函数。 predict = pd.where(pd.reduce_sum([[-1], [1]] * model, axis=0) < 0, -1, 1) # 创建预测函数计算引擎。 predict_engine = pd.Engine(predict) # 设置网格密度为0.1。 h = 0.1 # 生成预测采样点网格。 x, y = np.meshgrid(np.arange(np.min(c_x) - 1, np.max(c_x) + 1, h), np.arange(np.min(c_y) - 1, np.max(c_y) + 1, h)) # 绑定变量值。 predict_engine.bind = {A: [x.ravel(), y.ravel()]} # 生成采样点预测值。 z = predict_engine.value().reshape(x.shape) # 绘制图像。 plt.title('Paradox implement 2x4x2 Neural Network') plt.plot(c1_x, c1_y, 'ro', label='Category 1') plt.plot(c2_x, c2_y, 'bo', label='Category 2') plt.contourf(x, y, z, 2, cmap='RdBu', alpha=.6) plt.legend() plt.show() ``` 运行结果：  [回到顶部](#readme) ### 2x8x8x2神经网络螺旋型数据分类 ```python import numpy as np import matplotlib.pyplot as plt import paradox as pd # 每类随机生成点的个数。 points_sum = 100 # 产生一个互相