### 数据的概括性度量——统计学知识点详解
#### 一、引言
在数据分析领域,数据的概括性度量是统计学中的基础概念之一,它帮助我们理解数据集的基本特征,包括数据的集中趋势、离散程度以及分布形状等。这些度量不仅能够帮助我们快速了解数据的主要特点,还能为进一步的统计分析和建模提供重要的参考。
#### 二、集中趋势的度量
集中趋势的度量是指用来描述数据集中位置的统计量,主要包括众数、中位数和平均数。
**1. 众数**
- **定义**: 众数是一组数据中出现次数最多的数值。
- **表示**: 通常用M表示。
- **适用场景**: 适合数据量较多时使用,特别适用于分类数据,也可以用于顺序数据和数值型数据。
- **特点**:
- 不受极端值的影响。
- 一组数据可能没有众数或者存在多个众数。
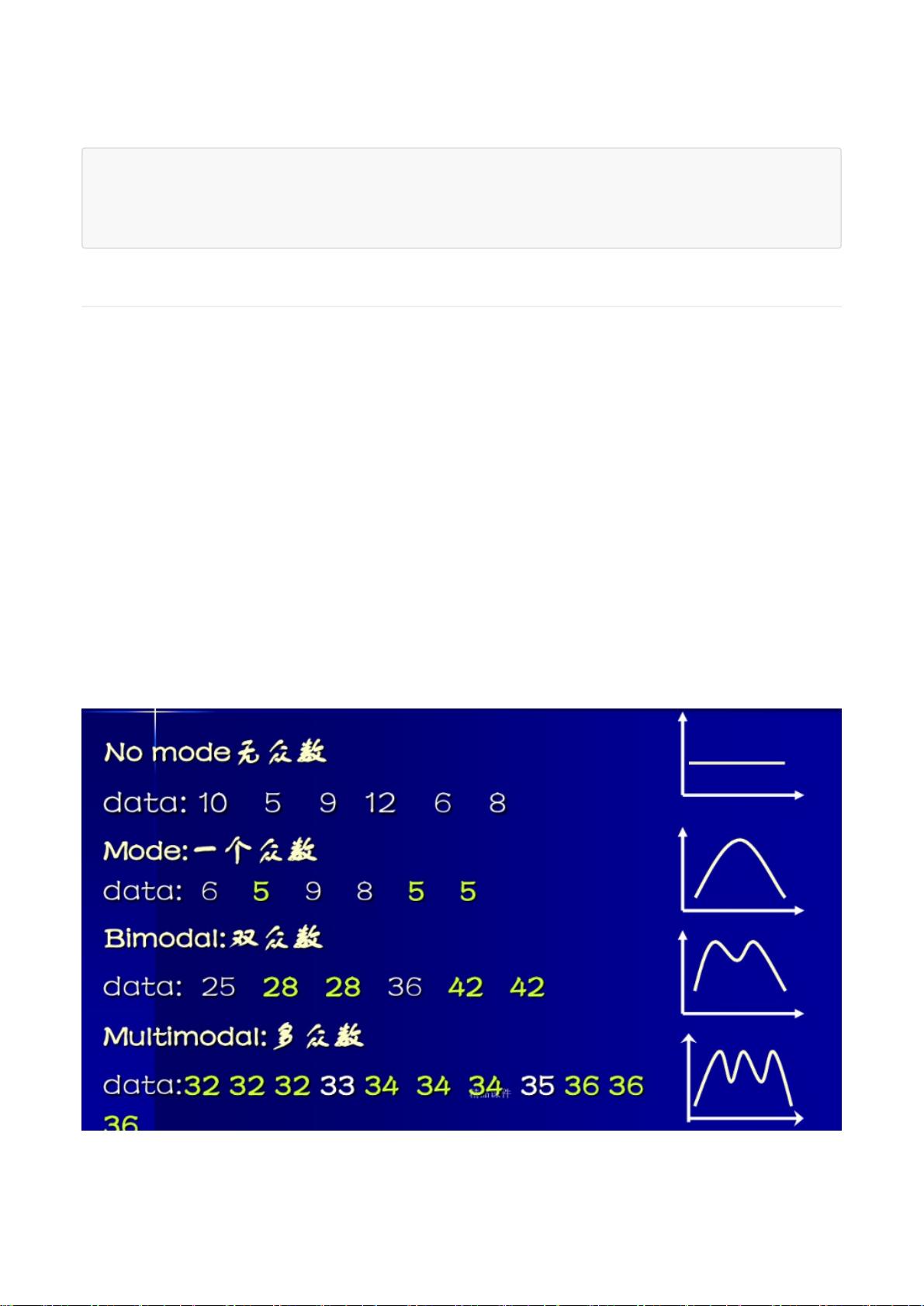
**2.1.1 众数的类型**
- 单峰众数:只有一个最高频率的值。
- 多峰众数:存在两个或两个以上的最高频率值。
- 无众数:所有数值出现的次数相同。
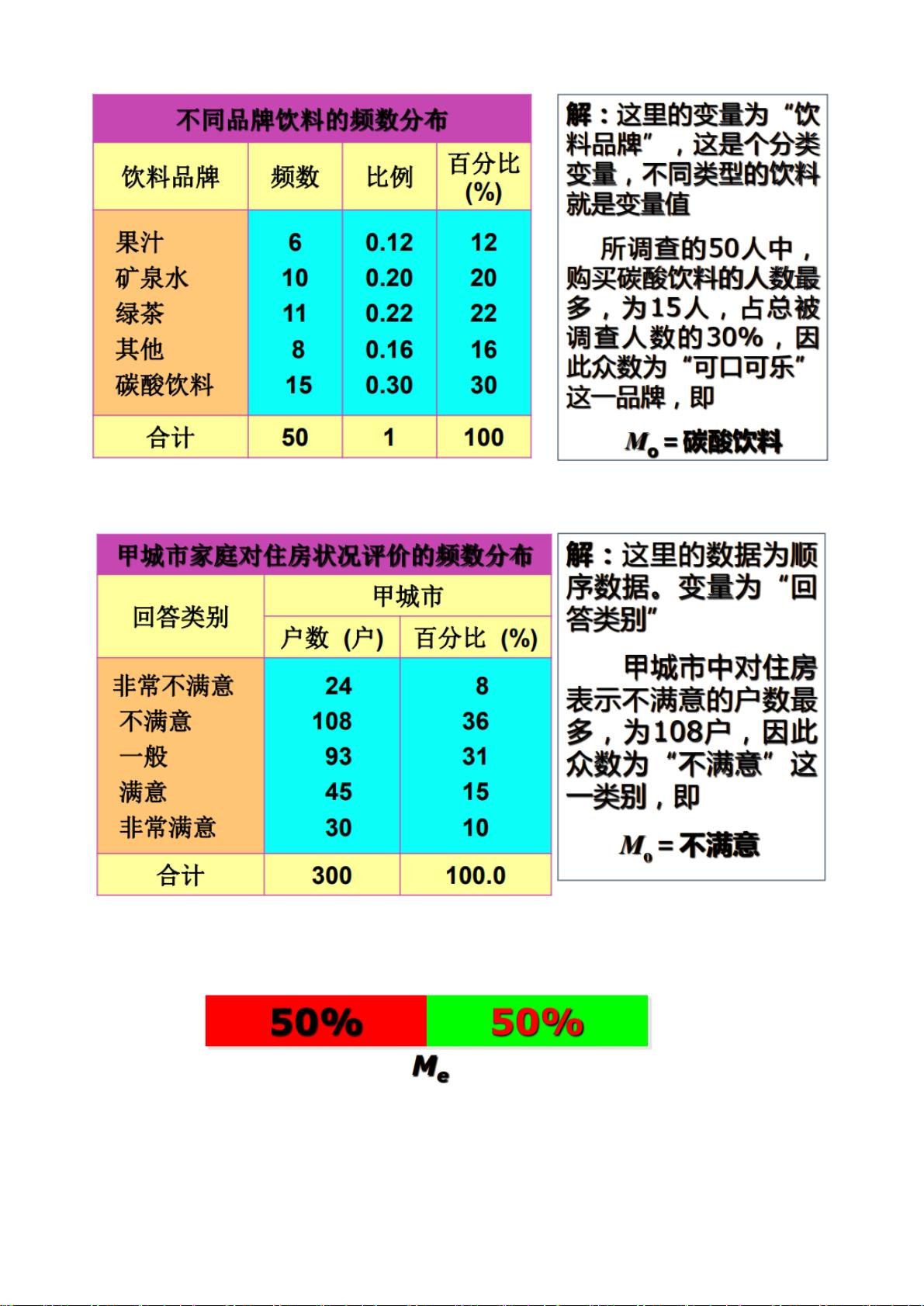
**2.1.2 分类数据的众数(例题分析)**
示例:在某项调查中,收集了人们对颜色偏好的数据。假设结果如下:红、蓝、绿、蓝、蓝、红、绿、红、蓝、绿。其中,“蓝”出现了3次,为最多,故“蓝”为该数据集的众数。
**2.2 顺序数据:中位数和分位数**
- **中位数**
- 定义:将数据按大小顺序排列后位于中间位置的数值。
- 特点:
- 不受极端值的影响。
- 适用于顺序数据,也可用于数值型数据,但不适合用于分类数据。
- 各变量值与中位数的离差绝对值之和最小。
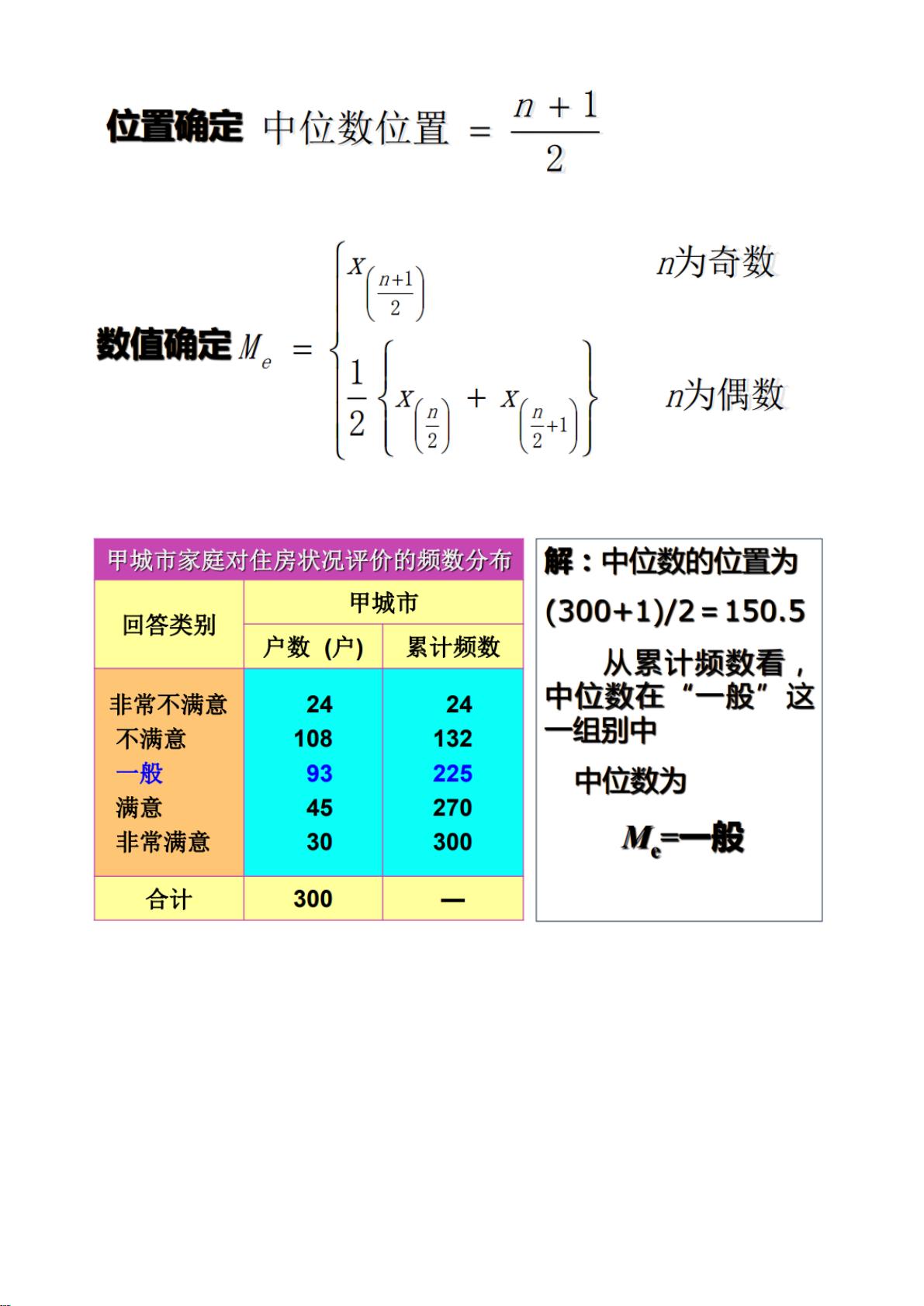
- **位置确定**:当数据量为奇数时,中位数位于正中间;数据量为偶数时,中位数为中间两个数的平均值。
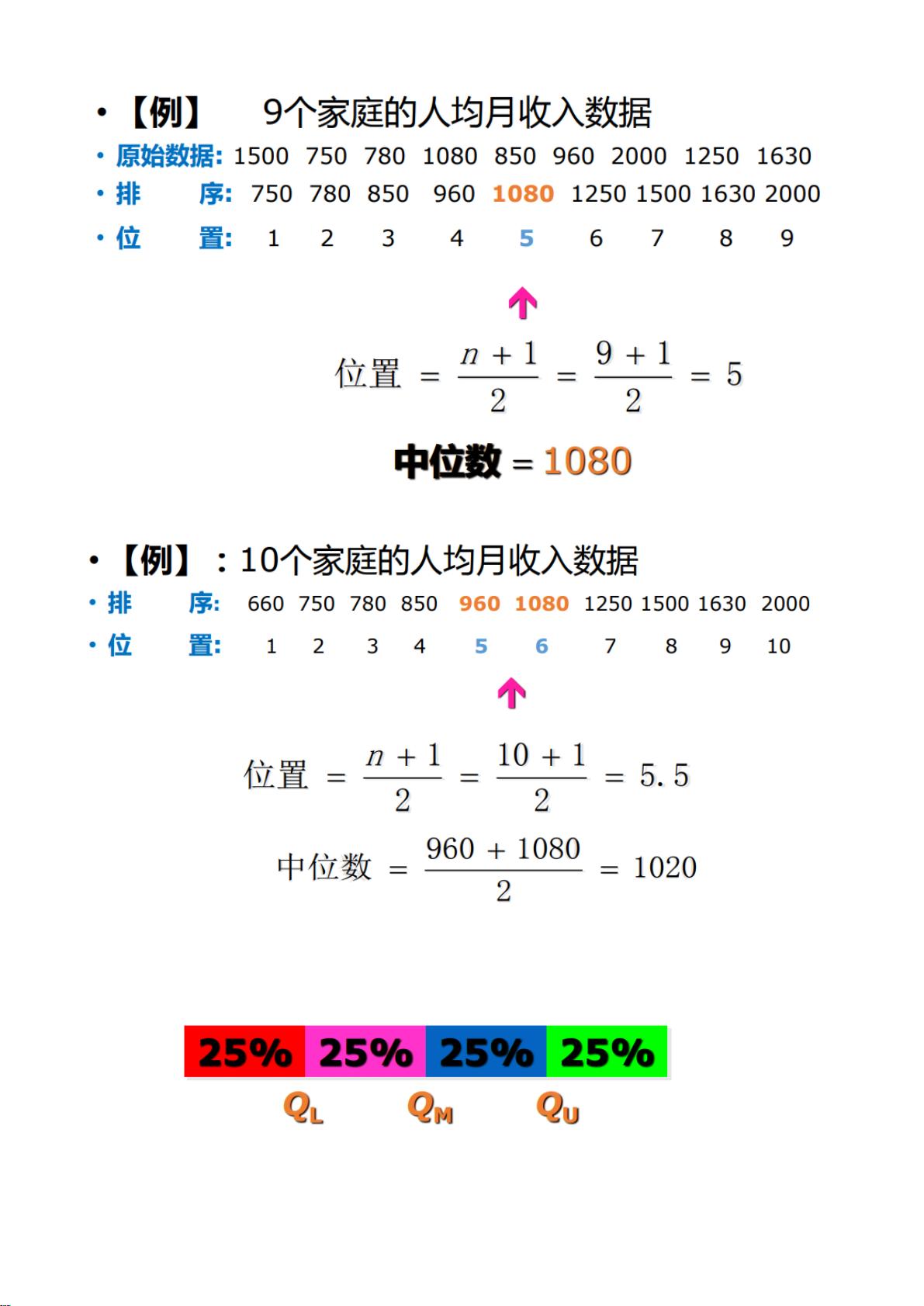
- **数值确定**:如数据量为9,则中位数为第5个数;若数据量为10,则中位数为第5个数和第6个数的平均值。
- **例题分析**:对于数据集{1, 3, 5, 7, 9},中位数为5;对于数据集{1, 3, 5, 7, 9, 11},中位数为(5+7)/2 = 6。
- **分位数**
- 定义:将所有数值从小到大排列并分成等份,处于各个分割点位置的数值即为分位数。
- **四分位数**:
- 下四分位数(QL):第25百分位数,即n/4处的位置。
- 上四分位数(QU):第75百分位数,即3n/4处的位置。
- **例题分析**:对于数据集{1, 2, 3, 4, 5, 6, 7, 8, 9},下四分位数为第3个数,即3;上四分位数为第7个数,即7。
**2.3 数值型数据:平均数**
- **算术平均数**
- 定义:所有数值的总和除以数值个数。
- 特点:
- 集中趋势的最常用测度值。
- 易受极端值影响。
- 包括简单平均数和加权平均数。
- **例题分析**:对于数据集{1, 2, 3, 4, 5},算术平均数为(1+2+3+4+5)/5 = 3。
**2.4 众数、中位数和平均数的比较**
- **适用数据类型**:
- 众数:适用于分类数据、顺序数据、数值型数据。
- 中位数:适用于顺序数据、数值型数据。
- 平均数:适用于数值型数据。
- **特点和应用**:
- 众数不受极端值影响,具有非唯一性,在数据分布偏斜程度较大且有明显峰值时使用。
- 中位数不受极端值影响,在数据分布偏斜程度较大时使用。
- 平均数易受极端值影响,数学性质优良,在数据对称分布或接近对称分布时使用。
#### 三、离散程度的度量
离散程度的度量是用来描述数据分散情况的统计量,主要包括异众比率、四分位差、方差和标准差等。
**3.1 分类数据:异众比率**
- **定义**:非众数组的频数占总频数的比例。
- **计算公式**:\[ \text{异众比率} = 1 - \frac{\text{众数频数}}{\text{总频数}} \]
- **适用场景**:用于衡量众数的代表性。
**3.2 顺序数据:四分位差**
- **定义**:上四分位数与下四分位数之差。
- **特点**:
- 反映了中间50%数据的离散程度。
- 不受极端值的影响。
- **计算公式**:\[ \text{四分位差} = \text{上四分位数} - \text{下四分位数} \]
**3.3 数值型数据:方差和标准差**
- **极差**:数据的最大值与最小值之差,是最简单的离散程度度量,但容易受到极端值的影响。
- **平均差**:各变量值与其平均数离差绝对值的平均数,能全面反映一组数据的离散程度,但数学性质较差。
- **方差和标准差**
- **定义**:数据离散程度的最常用测度值,反映了各变量值与均值的平均差异。
- **总体方差和标准差**:
- 方差:\[ \sigma^2 = \frac{\sum (x_i - \mu)^2}{N} \]
- 标准差:\[ \sigma = \sqrt{\sigma^2} \]
- **样本方差和标准差**:
- 方差:\[ s^2 = \frac{\sum (x_i - \bar{x})^2}{n-1} \]
- 标准差:\[ s = \sqrt{s^2} \]
- **自由度**:在计算样本方差时,由于样本均值的计算已经使用了一个数据点的信息,因此在计算方差时,有效数据点的数量减少了1,即自由度为n-1。
通过以上对集中趋势度量和离散程度度量的详细介绍,我们可以更深入地理解如何运用这些基本统计量来描述和分析数据。这些度量方法不仅是统计学的基础,也是进行高级统计分析和机器学习的前提。