没有合适的资源?快使用搜索试试~ 我知道了~
在2022年的美国数学建模竞赛(MCM)中,获得特等奖的B题研究聚焦于“水电共享”问题。参赛团队针对科罗拉多河流域的水资源分配挑战,提出了一个综合性的数学模型解决方案。科罗拉多河流域正面临降雨短缺和高温的困扰,因此需要制定一个合理且有说服力的水分配策略。
该研究建立了三个关键模型:
1. **多目标优化模型(Model I)**:考虑到水和电对于社会和经济目标的重要性,团队构建了一个包含四个目标的多目标优化模型。这四个目标可能包括确保基本生活用水、保障农业灌溉、支持工业生产和满足居民用电需求等。为了解决这个复杂的问题,团队采用了一种改进的遗传算法。这种算法能够有效地搜索解决方案空间,为两个大坝在一个月内的水电气供应量提供最佳配置。同时,通过引入时间作为变量,他们还能计算出满足这些需求所需的时间或补充量,这部分结果在表2中展示。
2. **AHP与TOPSIS结合评估模型(Model II)**:为了处理水与电之间的冲突,团队定义了公平系数,这涉及到不同州之间以及水与电之间的相对权重。AHP(层次分析法)用于量化这些因素之间的关系,而TOPSIS(技术评估中的最优选择法)则帮助确定最佳决策路径。通过这种方法,团队可以分析各种分配方案的相对优劣,确保在资源有限的情况下实现公平性与效率的平衡。
3. **单一目标线性规划模型(Model III)**:尽管没有详细说明,但这一模型可能是为了简化问题或特定场景下的决策,如优先满足某一特定目标,如人口最密集地区的用水需求。
在建立模型之前,团队收集了关于科罗拉多河流域的详尽水文数据,以及五个州的人口、工业产出、农业产量、GDP和电力需求数据。他们运用了数据可视化技术,使研究结果更直观易懂。
此外,团队还对过去十年五个州的水和电需求数据进行了傅立叶分析,揭示了这些数据的周期性变化规律。根据这一规律,他们建议模型应每三个月运行一次以适应需求变化。
综合来看,这个项目不仅涉及到了数学建模的理论与实践,还涵盖了优化理论、决策分析和数据处理等多个领域,是解决实际水资源管理问题的一个创新尝试。其方法论和解决方案对未来的流域管理和资源分配具有重要的参考价值。

Problem Chosen
B
2022
MCM
Summary Sheet
Team Control Number
XXXXXXX
Let Water Flow to the Optimal Allocation
Summary
Water or electricity? Arizona or California? Faced with continued rainfall shortages and high
temperatures, a rational and defensible water allocation strategy is critical for the Colorado River
Basin. Our team is glad to analysis and solve this problem mathematically.
Several models are established: Model I: Multi-Objective Optimization Model; Model II:
AHP and TOPSIS Combined Evaluation Model; Model III: Single Objective Linear Programming
Model, etc.
Before all the models are established, we looked up detailed hydrological data on the Colorado
River basin, as well as data on population, industrial and agricultural output, GDP and electricity
demand of five states. After we get the data, we applied a lot of data visualization methods in our
paper to make the results more intuitive.
For Model I: We have fully considered the role of water and electricity for social goal and
economic goal and established a Multi-Objective Optimization Model which has four objectives.
We focus on how to coordinate the work of two dams under complex constraints. We apply an
Improved Genetic Algorithm to solve our model, which makes the complex problem easier. And
we get the best solutions for how much water and electricity the two dams would provide to the five
states in a month’s time. On this basis, time is introduced as a variable to help calculate how much
time it will take, or how much supplyment should be provided to meet those needs by integral
equation(results are shown in Table 2).
In addition, we applied Fourier Analysis to process the data of water and electricity demand
of five states in the past ten years, and obtained the periodic change rule of these data, and then
concluded that our model should be run again every three months.
For Model II: In order to deal with the contradiction between water and electricity, we define
the Fairness Coefficient of water and electricity, then apply it to the solution of model I. We
use AHP and TOPSIS Combined Evaluation Model to caculate the fairness coefficient from 3
dimensions: conomic, social and ecological dimensions, which can not only solve the problems
that some indexes are difficult to quantify, but also ensure the objectivity of the fairness coefficient.
For Model III, We divided the degree of drought into four grades, defined the Economic Loss
Function, establish a Single Objective Programming Model, and worked out the water resources
allocation plan that minimizes the economic loss under the premise of guaranteeing the domestic
water. In the end, the experimental rules are summarized and general suggestions are provided.
As the three models mentioned above discuss rich factors and drought conditions, our model
has strong adaptability. It can be used not only in the area we are studying, but also in other places
like that. Finally, sensitivity analysis of supply and demand analysis shows that the model is
not sensitive to the mutual change, that is, it can provide the best allocation scheme for different
regions. At the same time, the robustness of the model is tested. When 10% random disturbance
is added, the maximum error is 4.723%, which proves its stability. Afterwards, a Budget Request
supported by our stable models has been written for CFA.
Keywords: Water Allocation; Multi-Objective Optimization; Improved Genetic Algorithm;
AHP and TOPSIS Combined Evaluation Model; Sensitivity Analysis

Team # XXXXXXX Page 2 of 21
Contents
1 Introduction 3
1.1 Problem Background . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.2 Literature Review . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.3 Our work . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2 Preparation of the Models 5
2.1 Assumptions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
2.2 Notations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
3 Multi-Objective Optimization Allocation Model 7
3.1 Optimized Objective: profit and demands . . . . . . . . . . . . . . . . . . . . . . 8
3.2 Constraints: rules and guidelines . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
3.3 Additional Discussion: time, supply and frequency. . . . . . . . . . . . . . . . . . 11
3.4 Results . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
4 Combined Evaluation Model 13
4.1 AHP for Scoring . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
4.2 TOPSIS for Evaluating . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
4.3 Model Transformation and Results . . . . . . . . . . . . . . . . . . . . . . . . . . 15
5 Model for Extreme Weather 16
6 Sensitivity and Robustness Analysis 17
6.1 Sensitivity Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
6.2 Robustness Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
7 Strengths and Weaknesses 18
7.1 Strengths . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
7.2 Weaknesses and Further Improvements . . . . . . . . . . . . . . . . . . . . . . . . 19
Better Allocation, Better Colorado 21
8 References 21
References 21
Team # XXXXXXX Page 3 of 21
1 Introduction
1.1 Problem Background
For hundreds of years, The Colorado River has nourished seven American states and two Mex-
ican states, known as "The Beating Heart of The American Southwest". Water is stored in two
major dams (Glen Canyon dam and Hoover dam) for agriculture, industry, residential use, to help
generate electricity, and for recreation and culture. But a crisis is looming. After decades of waste-
ful water management policies and practices, demand for the river’s water now exceeds its supply.
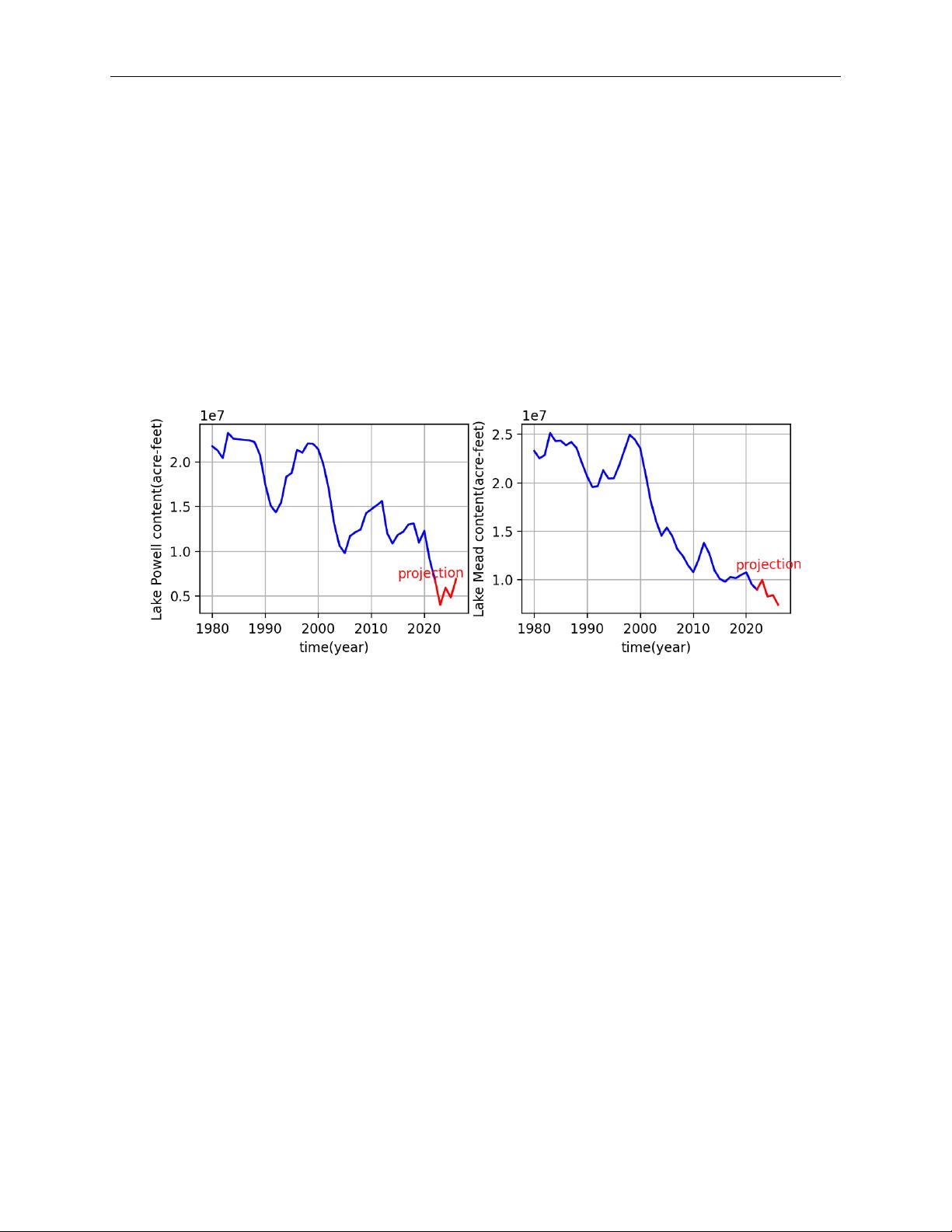
The water storage levels of the two dams ’corresponding lakes (Lake Powell and Lake Mead) have
been declining, as shown in Figure 1 , with a pessimistic projection by us.
Figure 1: Reservoir elevations for GC and Hoo dam
"Colorado, along with other Colorado River Basin states and the federal government, is prepar-
ing to negotiate a new set of operating guidelines that will go into effect after the other guidelines
expire." Without relying on any historical agreement or any organization, our team is happy to
provide the best mathematical solution for the region, which is based on scientific analysis. Using
our model, we can balance water and electricity storage between two dams, provide storage and
transportation solutions, and perform analysis under variable supply and demand.
Four major problems are discussed in this paper, which are:
• Build a mathematical model, providing storage and transportation solutions under fixed
supply and demand conditions, giving how much time and additional supply is required.
• Evaluate the factors, setting a standard that is used to address the competing interests be-
tween the general use of water and the electricity generation.
• Expand the model, considering solutions for situations where there is not enough water to
meet demand.
• Performed sensitivity analysis, giving the model’s indication under the technical composi-
tion or supply and demand changes.
Team # XXXXXXX Page 4 of 21
1.2 Literature Review
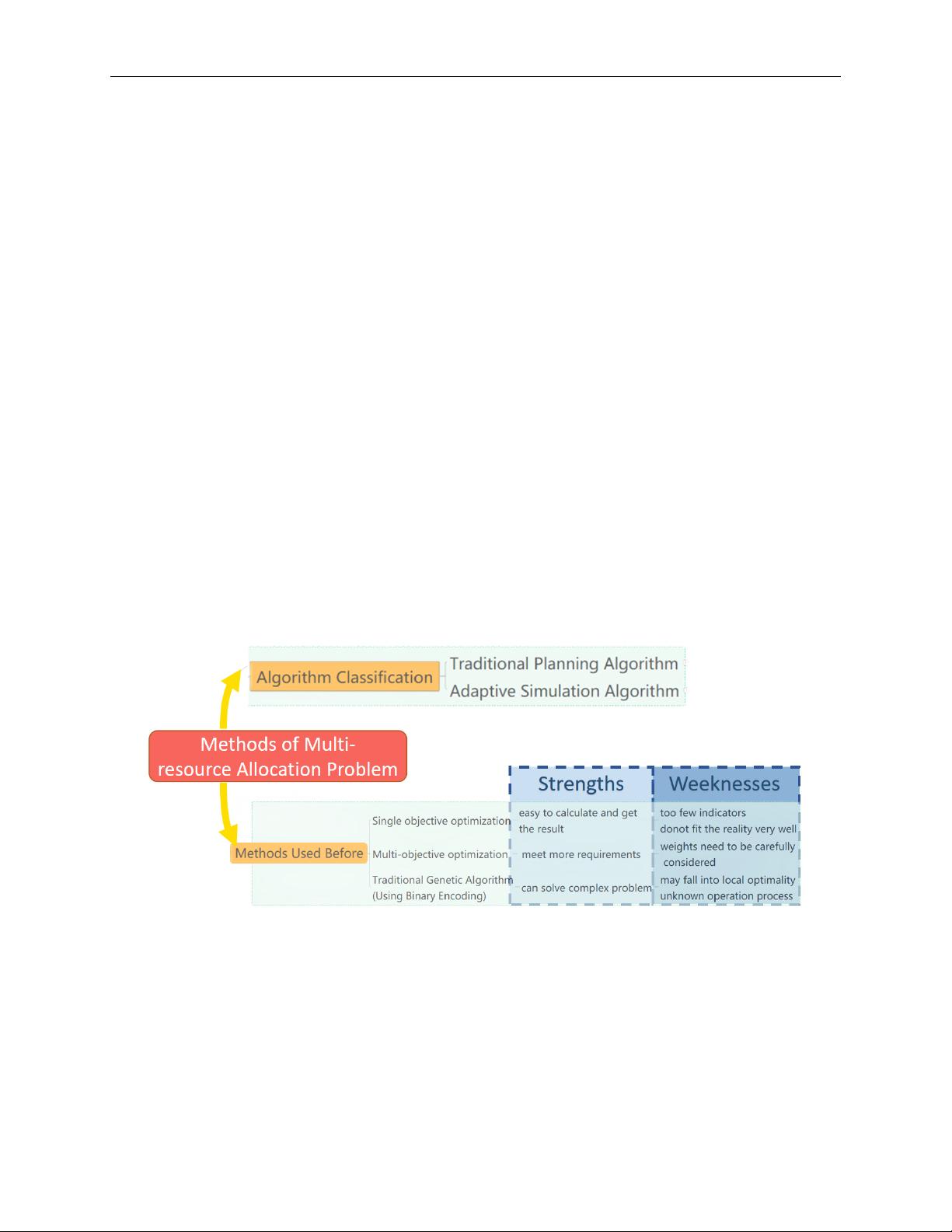
This question is mainly about the distribution of water and electricity between dams and states.
In recent years, research on optimization algorithms for planning is very hot, but there are not
many In the same field. Generally, solutions after model abstraction can be divided into two cate-
gories: traditional planning algorithm and adaptive simulation algorithm. This section mainly
discusses the three typical methods that have been proposed:
• Single objective optimization often takes the minimum economic loss as its goal. For
example[5], Zhao et al. investigated the GDP of agriculture and industry, weighted water
resources according to the proportion, and finally solved the problem through linear equa-
tions.
• There are a variety of metrics for multi-objective optimization. Different papers have dif-
ferent emphasis on the environment, ecology, society and other aspects. Such problems
are often sorted by evaluation methods and converted into the first type of problems[3], or
solved by complex equations[4].
• Bionics algorithms, such as genetic algorithm, obtain the optimal solution through contin-
uous randomization and screening. It is often suitable for more complex models[2], but
requires more data and constraints.
The strengths and weaknesses of these methods can be visually presented and is shown below:
Figure 2: Stage-capacity curve for GC and Hoo dam
1.3 Our work
• Establish a multi-objective programming model, fully considers social and economic ben-
efits, and uses genetic algorithm to solve it. On this basis, the flow-time curve was fitted to
calculate the time required to supply water and the amount of additional water required by
each state over time. And the frequency of the running model is determined by Fourier
variation.
剩余20页未读,继续阅读
资源推荐
资源评论
137 浏览量
2020-05-21 上传
133 浏览量
2023-02-24 上传
106 浏览量
133 浏览量
127 浏览量
151 浏览量
142 浏览量
133 浏览量
149 浏览量
资源评论

Can__er
- 粉丝: 2822
- 资源: 2
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功