考研数据结构第七章-图论必刷题

考研数据结构第七章-图论必刷题。 该文件里面一共有42道题，其中包括选择题，填空题和应用大题。这些题目都是历年各大名校的考研真题，非常具有参考意义。学完图论这章，只需要刷完这里面的题目就足够了。所有的知识点均包括。 【考研数据结构第七章-图论必刷题】这一部分主要涵盖了图论在数据结构中的重要知识点，包括图的基本概念、性质以及相关的算法。以下是详细的内容解析： 1. 图的路径定义：图中的路径是由顶点按顺序连接的边构成的序列。在选择题1中，正确答案是A，即由顶点和相邻顶点序偶构成的边所形成的序列。 2. 无向图的边数：无向图的边数最多为n(n-1)/2，这是因为无向图中每条边连接两个不同的顶点，所以题目中B选项正确。 3. 连通无向图的边数：一个n个顶点的连通无向图至少有n-1条边，这样才能确保所有顶点都连通。所以选择题3的答案是A。 4. 连通有向图的边数：要连通有n个顶点的有向图，至少需要n-1条边，对应选择题4，答案是A。 5. 完全有向图的边数：n个结点的完全有向图含有n*(n-1)条边，因此选择题5的答案是D。 6. 连通分量的数量：一个图最少有1个连通分量（当图是连通的），最多有n个连通分量（当图是不连通的，每个顶点是一个独立的连通分量），对应选择题6。 7. 度数与边数的关系：在无向图中，所有顶点的度数之和等于边数的两倍，而在有向图中，所有顶点的入度之和等于出度之和，选择题7的答案分别是B和C。 8. 有向无环图(DAG)与表达式的关系：表达式(A+B)*(A+B)/A可以用一个DAG来表示，至少需要5个顶点，对应选择题8的答案是A。 9. DFS遍历：深度优先搜索(DFS)遍历无环有向图，在退栈返回时打印顶点，会得到逆拓扑有序的结果，对应选择题9。 10. 稀疏图的存储结构：对于稀疏图，邻接表更适合表示，而邻接矩阵适用于稠密图。所以，选择题10的答案分别是D和E。 11. 邻接矩阵的对称性：无向图的邻接矩阵是对称的，对应选择题11。 12. 邻接矩阵的信息：从邻接矩阵可以读出顶点数，无向图的边数是矩阵对角线元素之和的一半，有向图的弧数也是矩阵非对角线元素之和的一半。对应选择题12的答案分别是A、D和B。 13. 顶点的度：在邻接矩阵表示的图中，顶点Vi的度是其对应行或列的非零元素个数，选择题13未给出具体矩阵，无法确定。 14. 路径的检查：在邻接矩阵中，检查距离为m的路径是否存在，需查看Am-1的第i行第j列元素。 15. 图的遍历特性：图的遍历是每个顶点只访问一次，有深度遍历和广度遍历两种方式，深度遍历是递归过程，适用于无环图。错误的选项是C，因为深度遍历也适用于有向图。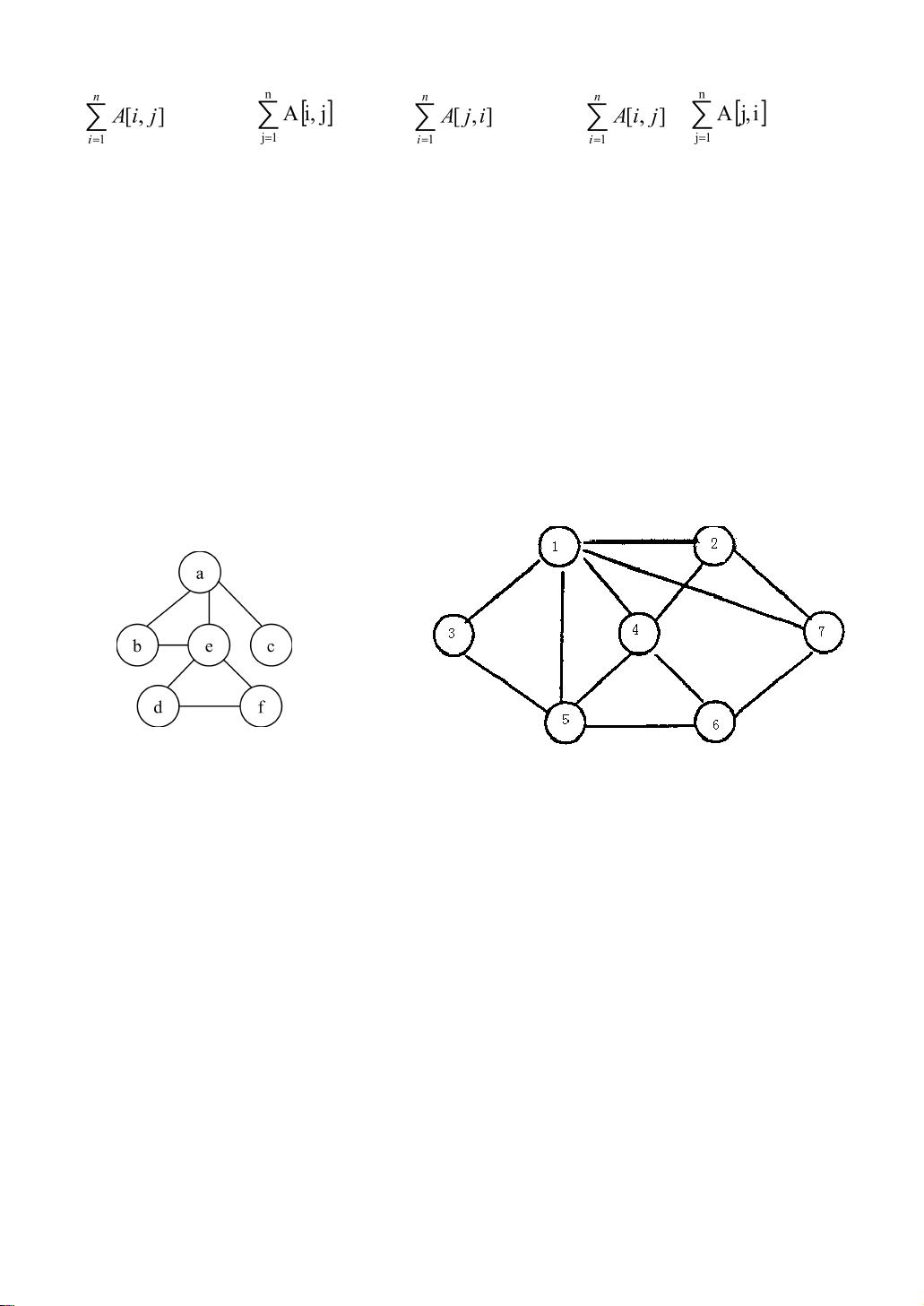 16. 深度优先遍历序列：在给定的无向图中，深度优先遍历得到的顶点序列可能是多种，例如B选项。 17. 符合深度优先遍历的序列：根据图的结构，可能存在多种深度优先遍历序列，正确答案是C。 18. 深度优先遍历与广度优先遍历序列：对于给定的无向图，从顶点1出发，深度优先遍历可能得到序列C，广度优先遍历通常得到有序序列，可能是B。 19. 判断有向图环的方法：拓扑排序可以判断有向图是否存在环，因此正确答案是B。 20. 邻接表的应用：邻接表是一种高效存储图的方式，尤其对于稀疏图，它节省空间且便于遍历。 以上就是关于考研数据结构第七章-图论必刷题中涉及的知识点详解，这些内容包括图的基本概念、性质、遍历算法以及图的存储结构等，是数据结构学习的重要组成部分，对于理解和解决实际问题有着重要的作用。