大学数学实验
Mathematical Experiments
实验10 回归分析
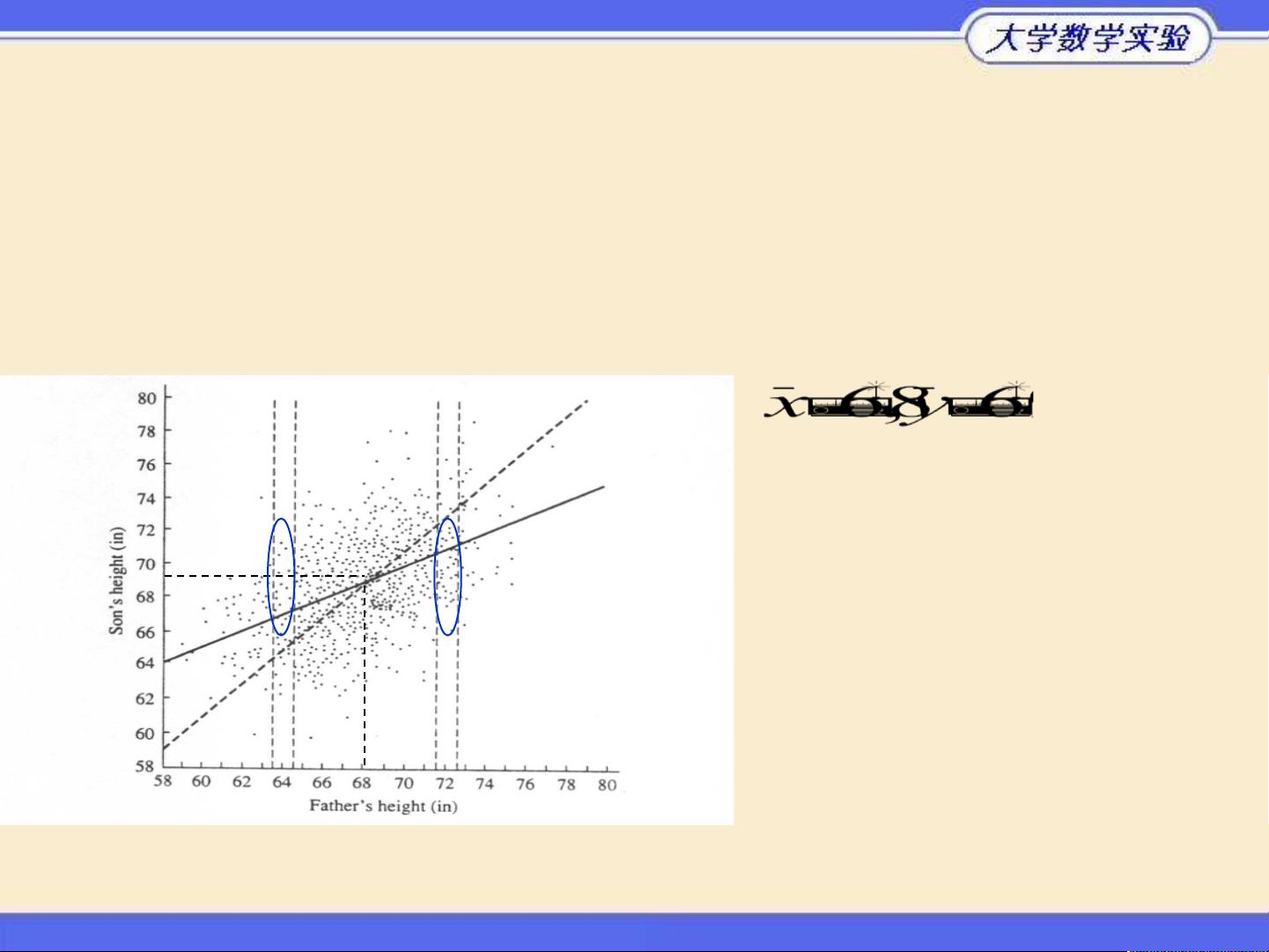
Pearson: 1078个父亲和儿子身高的散点图
回归(regression)?
Francis Golton (1822-1911)
•一般说来高个子的父代会有高个子的子代
•子代的身高比父代更加趋向一致(“向平庸的回归”)
对于身高72英寸的父亲,
儿子身高多数不到73英寸;
对于身高64英寸的父亲,
儿子身高多数超过65英寸;
回归直线 y=0.516 x+33.73
O
儿子比父亲平均高1英寸

• 由于客观事物内部规律的复杂及人们认识程度的限制,
无法分析实际对象内在的因果关系;
• 人们关心的变量(因变量)受另外几个变量(自变量)的关
联性(非因果性)的影响,并且存在众多随机因素,难以
用机理分析方法找出它们之间的关系;
•需要建立这些变量的数学模型,使得能够根据自变量
的数值预测因变量的大小,或者解释因变量的变化。
回归分析是数学建模的有力工具
血压与年龄 刹车距离与车速
薪金与资历、教育程度、工作岗位

• 收集一组包含因变量和自变量的数据;
• 选定因变量与自变量之间的模型,利用数据
按照最小二乘准则计算模型中的系数;
• 利用统计分析方法对不同的模型进行比较,
找出与数据拟合得最好的模型;
• 判断得到的模型是否适合于这组数据,诊断
有无不适合回归模型的异常数据;
• 利用模型对因变量作出预测或解释。
回归分析的主要步骤

1. 简化的实际问题及其数学模型
2. 一元线性回归
3. 多元线性回归
4. 非线性回归
回归分析(Regression Analysis)
•从应用角度介绍回归分析的
基本原理、方法和软件实现


















