线段树的课件 今天刚刚学了这个

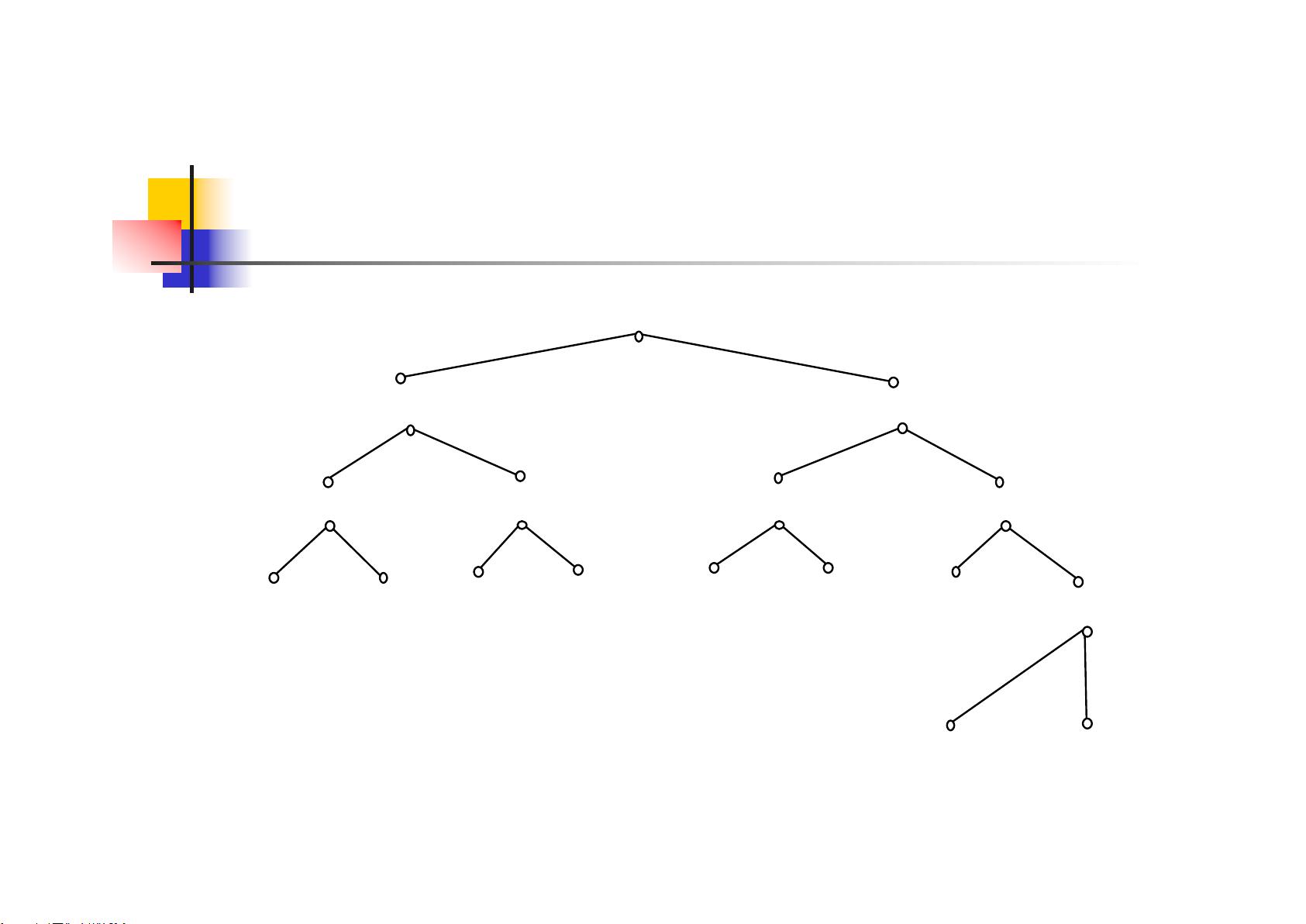
线段树，作为一种高效的数据结构，广泛应用于计算机科学与编程竞赛中，特别是在处理涉及区间查询或更新的问题上表现卓越。本文将深入解析线段树的基本概念、构建原理、应用场景及其实现方式，帮助读者全面理解这一重要数据结构。 ### 线段树的基本概念 线段树本质上是一种二叉树，其每个节点代表一个特定的区间，通常在直角坐标系的X轴上定义。线段树的核心优势在于能够快速进行区间操作，如查询区间内元素的和、最大值、最小值等统计信息，以及区间更新，例如修改区间内所有元素的值。这种数据结构通过递归地将区间划分为更小的子区间，从而实现高效的查询和更新。 ### 构建原理 线段树的构建遵循一定的规则，根节点通常代表整个区间，如\[1, N\]，其中N是序列的长度。每个内部节点的左右子节点分别表示其父节点区间的一半，具体而言，如果父节点的区间是\[a, b\]，那么左子节点的区间是\[a, (a + b) / 2\]，右子节点的区间是\[((a + b) / 2 + 1), b\]。这样的划分方式确保了每个子区间都是父区间的子集，并且所有的子区间最终会构成原区间的完全覆盖。通过这种方式，线段树能够在O(logN)的时间复杂度内完成区间查询和更新操作。 ### 应用场景 线段树的应用场景非常广泛，尤其是在解决区间问题上，包括但不限于： - **区间求和**：计算某个区间内所有元素的和。 - **区间更新**：对某个区间内的所有元素进行统一的加减操作。 - **区间最大/最小值查询**：找到某个区间内的最大或最小元素。 - **区间统计**：统计某个区间内满足特定条件的元素数量。 例如，在上述的“盒子阴影宽度”问题中，通过线段树可以快速计算出所有盒子投影在墙上的总宽度，即线段覆盖的总长度，而无需遍历每一个可能的交集，极大地提高了计算效率。 ### 实现方式 线段树的实现主要分为两种：基于指针的动态数据结构和基于数组的完全二叉树。 #### 动态数据结构 使用指针链接的动态结构，每个节点包含指向其左右子节点的指针，以及其他存储区间信息的域，如覆盖状态等。这种方法更加灵活，但可能因频繁的内存分配和回收导致额外的开销。 #### 完全二叉树 利用数组来模拟完全二叉树的结构，通常数组的大小为节点数的四倍，以预留足够的空间用于子节点的存储。对于数组中的任意节点i，其左子节点的索引为2 * i，右子节点的索引为2 * i + 1，父节点的索引为i / 2（向下取整）。这种方法避免了动态内存管理的开销，同时提供了固定的访问模式，使得查询和更新操作更加高效。 ### 总结 线段树作为处理区间问题的强大工具，通过其独特的构建原理和高效的数据结构设计，能够在多种场景下提供快速准确的解决方案。无论是编程竞赛还是实际应用，掌握线段树的原理和实现方法都将极大提升解决问题的能力和效率。通过不断实践和探索，线段树将成为开发者解决复杂区间问题的重要武器。