xiaob0_lecture

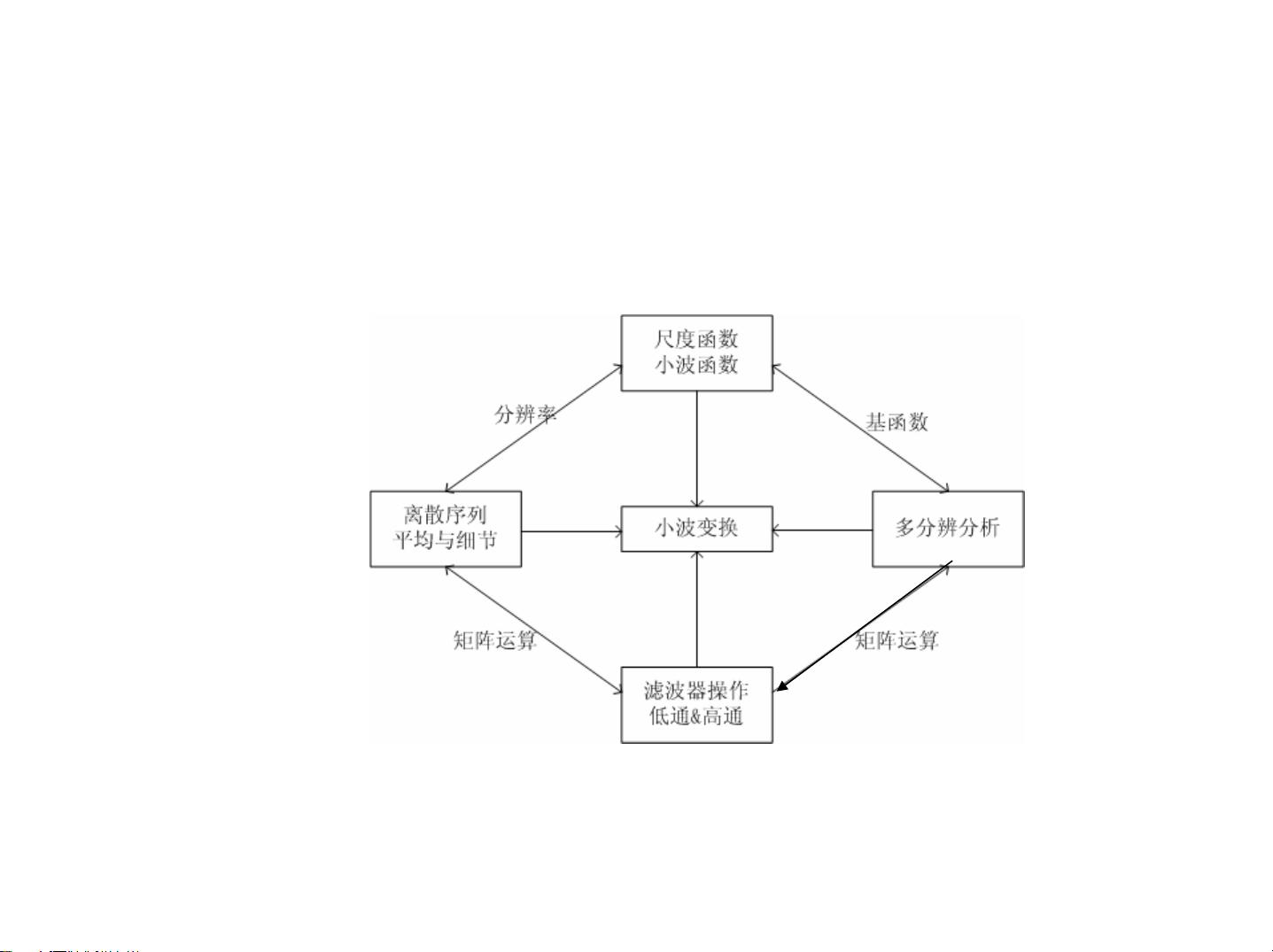
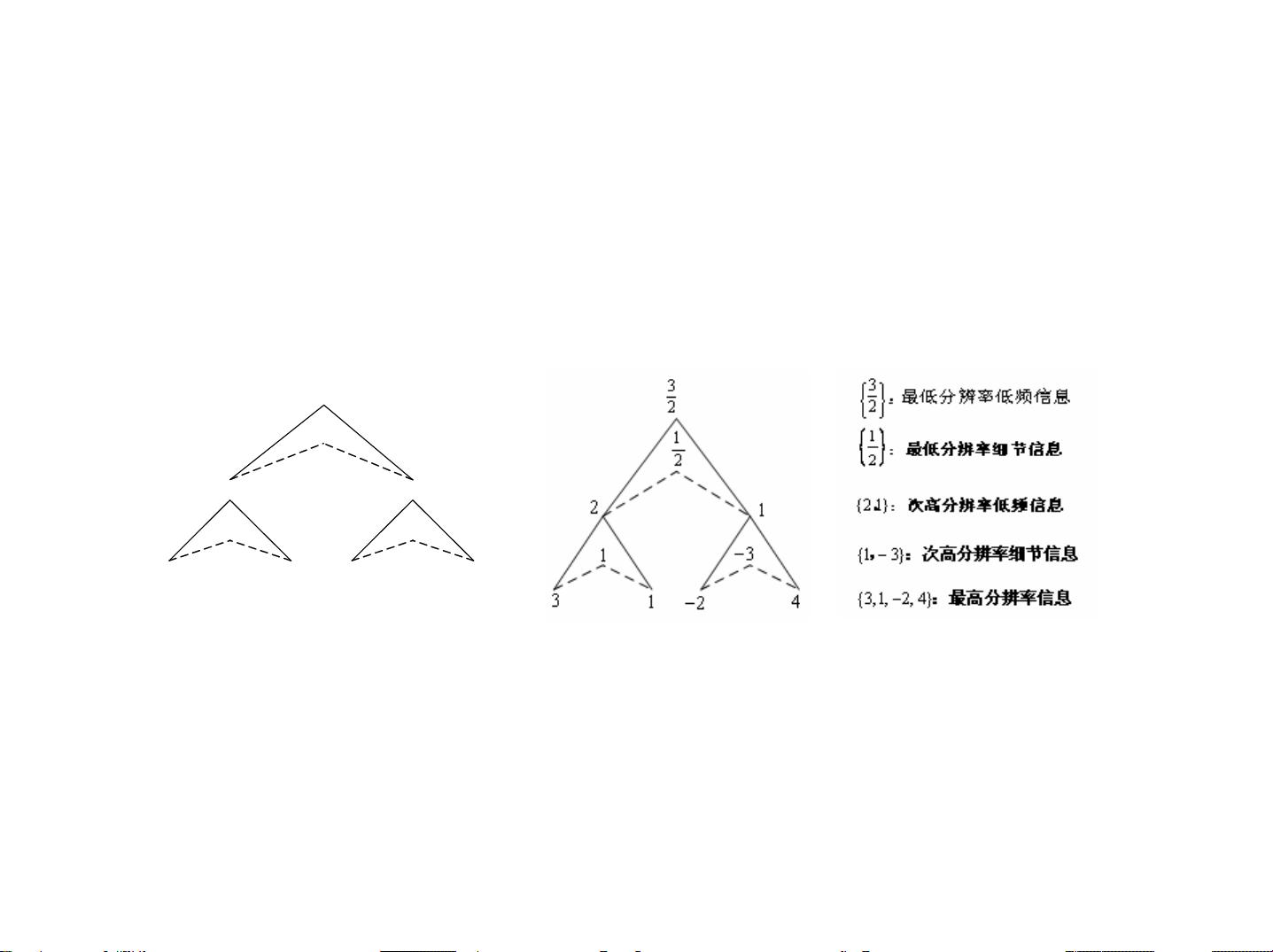
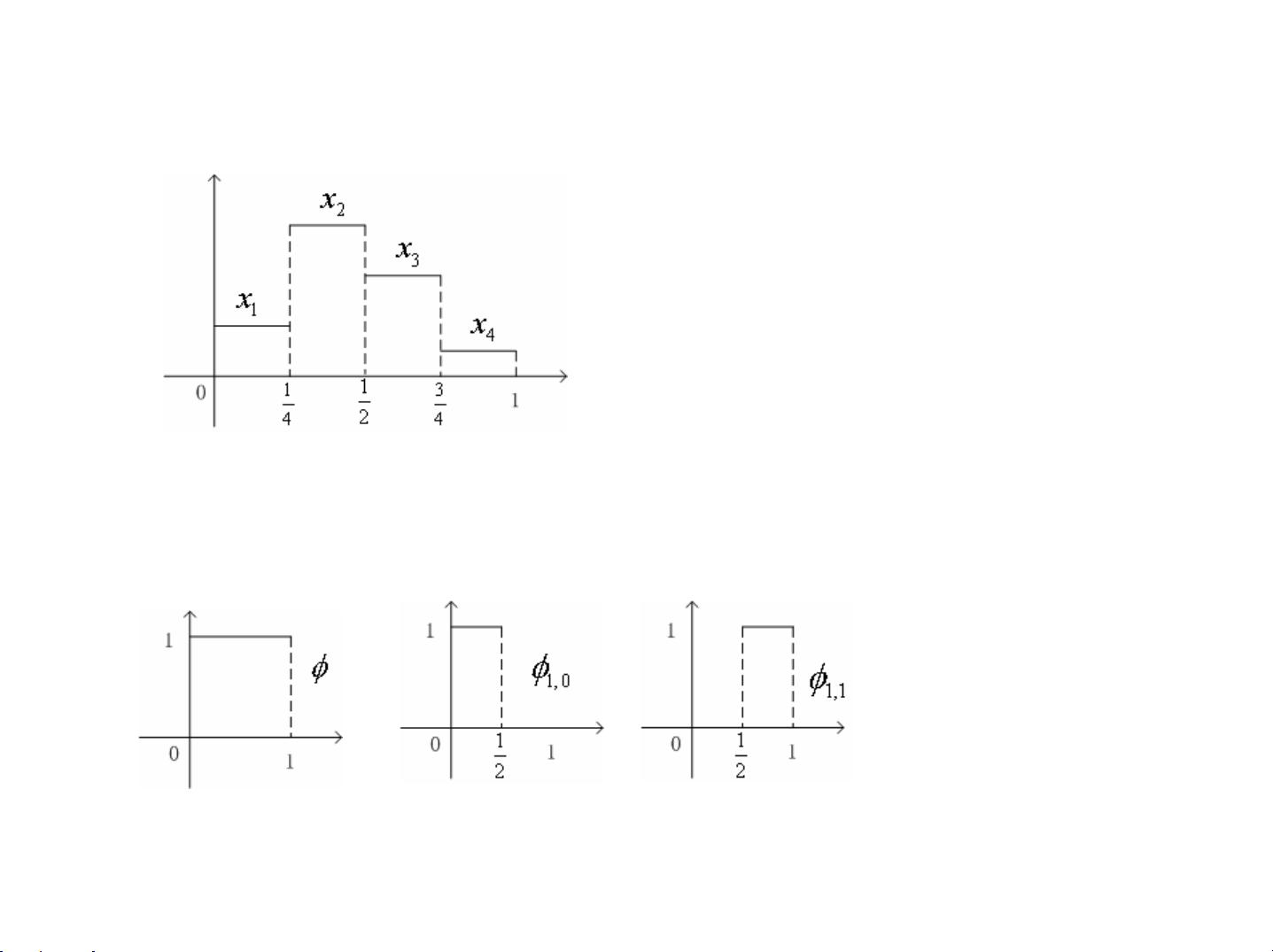
### 小波分析及其工程应用 #### 孙延奎 教授 清华大学计算机系 2009年3月3日 本讲座旨在深入探讨小波分析的基础理论及其实用价值，尤其是在工程领域的应用。小波分析作为一种强大的数学工具，在图像处理、信号分析、数据压缩等多个领域都有着广泛的应用前景。 ### 第1章 Haar小波分析 #### 1.1 前言 小波分析的核心思想是通过对信号进行多分辨率分析，将信号分解为不同频率的成分，从而实现对信号特性的精细控制和理解。这种分析方法能够有效地捕捉到信号中的局部特征，为后续的数据处理提供便利。 #### 1.2 平均与细节 在小波分析中，通常会将原始信号分解为一系列的“平均”信号和“细节”信号。这里的“平均”信号是指信号的低频部分，而“细节”信号则是指信号的高频部分。通过对信号进行这样的分解，可以更加直观地理解和处理信号中的各种成分。例如，在图像处理中，低频部分通常代表图像的基本轮廓和颜色分布，而高频部分则包含图像的细节和边缘信息。 #### 1.3 尺度函数与小波函数 尺度函数（scale function）和小波函数（wavelet function）是小波分析中的两个核心概念。它们分别用于表示信号的多分辨率表示中的低频部分和高频部分。具体来说： - **尺度函数**：尺度函数 φ(t) 是一种用于表示信号的低频成分的函数。它可以看作是信号的平滑版本。 - **小波函数**：小波函数 ψ(t) 则用于表示信号的高频成分，即信号中的细节部分。 这两种函数的结合可以用来表示任何连续函数 f(t)，并通过一个多分辨率分析框架来描述。在这个框架中，信号可以被表示为不同层次的尺度函数和小波函数的线性组合，从而形成信号的多分辨率表示。 ##### 多分辨表示 在多分辨表示中，一个函数可以被分解为不同尺度下的低频成分和高频成分。这种表示方式不仅有助于我们理解信号本身的结构，还可以用于数据压缩等实际应用中。 ##### 两尺度方程 尺度函数和小波函数之间存在密切的关系，可以通过所谓的两尺度方程来表示： \[ φ(t) = \sum_{k} h(k) φ(2t - k) \] 这里，\(h(k)\) 是一组系数，这些系数决定了尺度函数如何通过自身缩放和平移来构造出新的尺度函数。 同样地，小波函数也可以通过尺度函数来表示： \[ ψ(t) = \sum_{k} g(k) φ(2t - k) \] 其中，\(g(k)\) 是另一组系数。 ##### 示例 以Haar小波为例，可以具体展示如何通过尺度函数和小波函数来表示信号。例如，在一个简单的例子中，原始信号 \(f(t)\) 可以表示为： \[ f(t) = a_0(t) + d_0(t) + d_1(t) \] 其中，\(a_0(t)\) 表示最粗层次上的平均值，而 \(d_0(t)\) 和 \(d_1(t)\) 分别表示不同层次上的细节信号。 #### 1.4 多分辨分析 多分辨分析进一步将信号的表示扩展到了函数空间的角度。在这个框架下，信号被看作是在不同尺度下的尺度空间 \(V_n\) 和小波空间 \(W_n\) 的元素。尺度空间包含了信号的所有低频成分，而小波空间则包含了信号的高频成分。 - **尺度空间**：\(V_n\) 定义了在特定尺度上信号的低频成分。 - **小波空间**：\(W_n\) 则定义了在同一尺度上信号的高频成分。 这两个空间的结合可以完整地表示信号的所有频率成分。例如，对于任意的 \(n\)，都有： \[ V_n = V_{n-1} \oplus W_{n-1} \] 这意味着，信号在 \(V_n\) 中的表示可以被分解为其在 \(V_{n-1}\) 中的低频表示和 \(W_{n-1}\) 中的高频表示之和。 通过这种方式，我们可以将信号逐步分解为不同分辨率下的表示，并根据需要对信号进行处理和分析。 小波分析是一种非常强大且灵活的信号处理工具。它不仅可以帮助我们更好地理解信号本身，还能应用于诸如图像压缩、噪声去除、边缘检测等多种实际场景中。随着计算能力的不断增强和技术的不断进步，小波分析的应用范围将会更加广泛。