OptimalTrajectoryGenerationforAutonomousVehicles资源-CSDN文库

自动驾驶

轨迹规划

需积分: 9 148 浏览量 2021-08-17 17:54:33 上传评论收藏 518KB PDF 举报

资源推荐

资源详情

资源评论

Optimal Trajectory Generation for Autonomous Vehicles Under

Centripetal Acceleration Constraints for In-lane Driving Scenarios

Yajia Zhang*, Hongyi Sun, Jinyun Zhou, Jiangtao Hu, Jinghao Miao

Abstract— This paper presents a noval method that gener-

ates optimal trajectories for autonomous vehicles for in-lane

driving scenarios. The method computes a trajectory using

a two-phase optimization procedure. In the ﬁrst phase, the

optimization procedure generates a close-form driving guide

line with differetiable curvatures. In the second phase, the

procedure takes the driving guide line as input, and outputs

dynamically feasible, jerk and time optimal trajectories for

vehicles driving along the guide line. This method is especially

useful for generating trajectories at curvy road where the

vehicles need to apply frequent accelerations and decelerations

to accommodate centripetal acceleration limits.

I. INTRODUCTION

Trajectory planning is an important component in au-

tonomous driving systems (ADS). It plays a critical role

on safety and comfort. Safety is of top priority as any

collision might lead to hazardous situations. Assuming pre-

dicted trajectories of surrounding obstacles are given from

upper stream module of ADS, path-time obstacle graph is

a commonly used tool for collision avoidance analysis if

future path of the autonomous driving vehicle (ADV) is

determined. This method projects the predicted trajectories of

surrounding obstacles onto the spatio-time plane and forms

path-time obstacles which specify at which time the further

path of the ADV would be on collision. The free area forms

the collision-free zone for trajectory planning. This method

is particularly useful for autonomous vehicles in structured

road scenarios. It fully utilizes the domain knowledge, as

most vehicles are driving along lanes. The method we pro-

pose adopts path-time-obstacle graph in collision avoidance

analysis and always plans a trajectory that lie within the

collision-free zone.

Comfort is another goal to achieve for ADS. Several

factors affect and are used to measure the comfort of one

trajectory. Acceleration and acceleration change rate (com-

monly known as jerk) are most commonly used metrics for

vehicle trajectories. Furthermore, depending on the direction,

human weight acceleration and jerk signiﬁcant differently for

longitudinal and lateral movement. Acceleration and jerk in

lateral direction must be bounded and minimized. For driving

along a curvy road, the longitudinal speed must be adjusted

frequently according to the curve, i.e., the curvature of the

road. A driving guide line is an abstraction of the road

center line, which contains the geometrical information of

the road. We assume the target of the autonomous vehicle

in-lane driving is following the driving guide line. To achieve

Yajia Zhang, Hongyi Sun, Jinyun Zhou, Jiangtao Hu, Jinghao Miao are

with Baidu USA LLC, 250 Caribbean Drive Sunnyvale, USA *Correspond-

ing author: Yajia Zhang zhangyajia@baidu.com

comfortable riding experience, the vehicle needs to accelerate

and decelerate according to the curvature of the driving guide

line. In our proposed method, the algorithm can directly

consider the geometrical information of the driving guide

line.

Optimization is a common approach in trajectory gen-

eration as it takes the objective or cost function and con-

straints directly into trajectory generation. For high degrees

of freedom (DOFs) conﬁguration space, optimization for

trajectory generation is generally slow and prone to local

minima, it is generally suitable for lower dimensional vehicle

conﬁguration space. In our method, we use a two-phase

optimization procedure. Each one intends to solve a subset of

trajectory generation problem. In this way, it greatly reduces

the overall complexity of optimization. For the ﬁrst phase,

our method generates a smooth driving guide line for ADV

to follow; in the second phase, the optimization procedure

takes the collision-free zone resulted from path-time obstacle

graph analysis and the close-formed driving guide line as

input, and generates a collision-free and comfort trajectory

that minimizes longitudinal acceleration, and centripetal ac-

celeration and jerk.

II. RELATED WORK

Trajectory planning is a critical component in autonomous

driving systems. Recently, a number of algorithms [7], [8],

[10] have been developed since DARPA Grand Challenge

(2004, 2005) and Urban Challenge (2007).

Randomized planners such as Rapidly Exploring Random

Tree (RRT)[6] are intended to solve high-DOF robot motion

planning with differential constraints. However, it is difﬁcult

for randomized planners to utilize the domain knowledge

from the structured environment for quickly convergence.

Nevertheless, the computed trajectory is generally low qual-

ity and thus cannot be used directly without a post-processing

step. Recent research on optimal randomized planner, such as

[3], can produce high-quality trajectories given enough plan-

ning time. But the convergence to optimal trajectory takes

rather long time thus it cannot be used in the dynamically

changing environment.

Discrete search method [5] computes a trajectory by

concatenating a sequence of pre-computed maneuvers. The

contatenation is done by checking whether the ending state

of a maneuver is sufﬁciently close to the starting state of

the target maneuver. This method generally works well for

simple environment such as highway scenarios. However, the

number of required maneuvers needs to grow exponentially

in order to solve complex urban driving cases.

2019 IEEE Intelligent Transportation Systems Conference (ITSC)

Auckland, NZ, October 27-30, 2019

The work in [13] runs an quadratic programming pro-

cedure in global/map frame. The trajectory is ﬁnely dis-

cretized in Cartesian space. The positional attributions of the

trajectory are directly used as optimization variables, and

outputs a trajectory that minimizes the objective function

which combines the measurement of safety and comfort.

The advantage of using optimization is it provides direct

enforcement of optimality modeling. The dense discretization

approach provides maximal control of trajectory to tackle

complex scenarios.

In [12], trajectory planning is performed in Frenet frame.

Given a smooth driving guide line, this method decouples

the movement of vehicle in map frame into two orthogonal

movements, one longitudinal movement that along the driv-

ing guide line and one lateral movement that perpendicular

to the guide line. For both movements, the trajectories are

generated using random samples, i.e., the end conditions

and parameter are discretized into certain resolution. The

sampled end conditions are directly connected with the

initial condition using quintic or quartic polynomials. Then

these longitudinal and lateral trajectories are combined and

selected according to a predeﬁned cost function.

The major drawback with the method is it lacks control of

the trajectory. For complex driving scenarios, it is difﬁcult for

this method to generate feasible trajectories. Nevertheless,

some caveats of using polynomial include problems with

stopping, unexpected acceleration and deceleration. To tackle

complex problems in real world, we need to maximize our

ability of controlling the trajectory. Thus, optimization is

a promising direction as constraints in the task domain

can be directly considered in trajectory generation. Exist-

ing optimization-based methods such as [13] [9] runs the

optimization in map frame.

The overall algorithm framework we proposed is similar

to the one in [12], however, we use optimization to solve the

1d planning problems, which greatly enhances the ﬂexibility

of the trajectory.

The method we present hybrids the Frenet frame trajectory

planning framework and optimization-based trajectory gener-

ation. Also, the trajectory optimization is performed in two-

phases, where each phase is a lower dimensional problem. In

this proposed method, the difﬁculty of optimization is greatly

reduced.

III. PROBLEM DEFINITION

The conﬁguration for a vehicle with differential constraints

in Cartesian space can be represented using three variables,

(x, y, θ), where x, y specify the coordinate of some reference

point for the vehicle and θ speciﬁes the vehicle’s heading

angle in the Cartesian space. In our work, we incorporate

one more dimension κ, which is the instant curvature resulted

from vehicle’s steering, into the conﬁguration space for more

accurate conﬁguration modeling, and hence the computed

trajectory provides additional information that can be used

for better designing the feedback controller. Trajectory plan-

ning for non-holonomic vehicles is essentially ﬁnding a

(

)

()

)

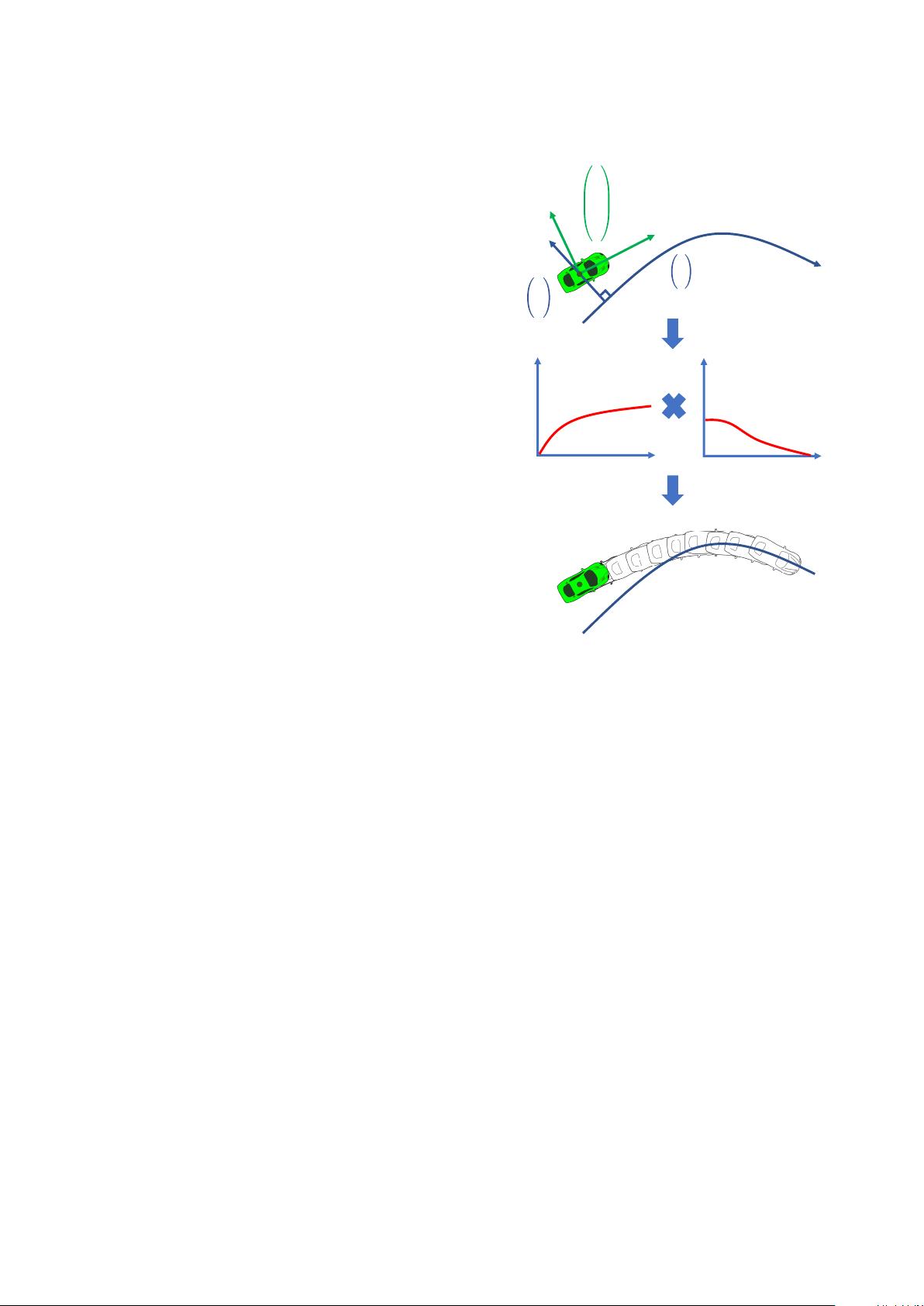
Fig. 1. Illustration of vehicle trajectory planning in assist of Frenet frame.

First, the vehicle dynamic state (x, y, θ, κ, v, a), which represents vehicles

position, heading, steering angle, velocity and acceleration, respective,

is projected on to a given driving guide line to obtain its decoupled

states in Frenet frame. (s, ˙s, ¨s) represents the vehicle state, i.e., position,

velocity and acceleration, along the guide line (i.e., longitudinal state) and

(d,

d) represents the vehicle state, i.e., position, velocity and acceleration,

perpendicular to the guild line (i.e., lateral state). Then, plan longitudinal

and lateral motions independently. Finally, longitudinal and lateral motions

in Frenet frame are combined and transformed to a trajectory in Cartesian

space.

function τ (t) that maps a time t to a speciﬁc conﬁguration

(x, y, θ, κ).

Trajectory Planning in Frenet frame

Our method adopts a similar framework as in [12], which

utilizes the concept of Frenet frame for trajectory planning

(see Fig. 1). Given a smooth driving guide line, a Frenet

frame decouples the vehicle motions in Cartesian space into

two independent 1D movements, longitudinal movement that

moves along the guide line and lateral movement that moves

orthogonally to the guide line. Thus, a trajectory planning

problem in Cartesian space is transformed to two lower

dimensional and independent planning problems in Frenet

frame. This framework exploits the task domain that most

vehicles are moving along the lane, and it is particularly

advantageous as it greatly simpliﬁes problem by reducing

the dimensionality of planning.

We assume that the autonomous vehicle is roughly driving

around the guild line. The main task for in lane driving is

to generate a trajectory for the autonomous vehicle driving

3620

剩余7页未读，继续阅读

评论收藏

内容反馈

zhaoqi暮宿

粉丝: 0
资源: 5

Optimal Trajectory Generation for Autonomous Vehicles

Optimal Trajectory Generation for Dynamic Street Scenarios in a Frenet Frame

Optimal Trajectory Generation for Dynamic Street Scenarios in a Frene´t Frame

Model Predictive Stabilization Control of High-speed Autonomous Ground Vehicles

Trajectory Generation and Control for Quadrotors

Optimal trajectory generation for dynamic street scenarios in a Frenet Frame.rar

Optimal Control Theory for Applications

Optimal Trajectory in a Frenet Frame

Optimal-Trajectory-generation-for-Lane-Changing-in-Frenet-Frame-master.zip

Optimal Kalman Filtering for System with Unknown Inputs

Howard 和 Kelly - 2007 - Optimal Rough Terrain Trajectory Generat

Optimal-Scheduling-for-Charging-and-Discharging-of-Electric-Vehicles-master.zip

一种沿完全指定路径的时间最优轨迹规划 的二分算法_C++_代码_下载

Optimal trajectory generation.zip

Optimal Transport for Applied Mathematicians.pdf

Intelligent Optimal Adaptive Control for Mechatronic Systems

Reinforcement Learning for Optimal Feedback Control

优化觅食算法 Optimal foraging algorithm for global optimization（OFA）

路径规划论文 --英文

Optimal Transport for Domain Adaptation

自主驾驶车辆

A Pseudospectral Strategy for LCM of Automated Vehicles on Highway

Distributed Optimal Consensus Control for Multiagent Systems With Input Delay

Optimal Training Sequence for MIMO Wireless

Distributed Optimal Kalman Filtering for

A multi-phase DMOC-based optimal trajectory generation methodology for a quadrotor.

最新资源

一种沿完全指定路径的时间最优轨迹规划的二分算法_C++_代码_下载