分段函数的解析式借鉴.pdf
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
分段函数是数学中一种特殊的函数形式,它由多个不同规则的函数段组合而成,每一段函数在特定的自变量区间内定义。在处理分段函数时,我们需要根据不同的自变量值选择相应的函数表达式来求解问题。以下是对题目中各知识点的详细解释: 1. 若一个二次函数g(x)使得f(g(x))的值域为[0,+∞),由于f(x)的值域被限制在了非负区间,那么g(x)的值域需包含f(x)的定义域中的最小值,即0。这意味着g(x)的最小值应为使f(x)=0的那个x值。 2. 对于函数的性质: - ①xxxf12有意义,这通常表示某个函数在特定的x值下有定义。 - ②函数是其定义域到值域的映射,这是函数的基本概念,每个定义域内的x值对应唯一一个值域内的y值。 - ③函数 y=2x(x∈N)的图象是一条直线,但因为x只取自然数,所以是离散的点构成的直线。 - ④函数0,0,22xxxxy的图象是抛物线,这表明函数的最高次项为2次,形成抛物线形状。 3. 动点P在直角梯形ABCD中移动,题目给出了函数y=f(x)的图象,通过分析图形可以求解三角形ABP的面积,从而得到△ABC的面积。 4. 函数y=|x^2-2x-t|在[0,3]上的最大值为2,需要考虑绝对值内部函数的极值和边界值,找出使函数取最大值的x值。 5. f(f(-2011))的计算需要先确定f(-2011)的值,然后将这个值代入f(x)中再次计算。 6. 函数g(x) = (x-1)f(x)是两个分段函数的组合,需要分别在O到A和A到B的区间上计算g(x)的最大值。 7. 已知f(-1) = 1和f(0) = -2,函数g(x) = f(x) + x的零点个数可以通过分析f(x)的图象与直线y=-x的交点数量得出。 8. 若f(f(0)) = 4a,首先求f(0),然后将结果代入f(x)求a的值。 9. 画出1-xH的图象,这涉及到一次函数的图象绘制。 10. 求函数g(x) = x^2-2在xg,4,上的值域,需要分析xg的取值范围和二次函数的性质。 11. 对于函数f(x) = 2-x-x^2,根据fK(x) = f(x)对任意x恒成立,可以找到K的值,使得f(x)在[0,+∞)上恒等于fK(x)。 12. 若f(1) + f(a) = 2,考虑到f(x) = sin(x)在[0,2π]上的性质,可以求解a的可能值。 13. 当xf关于x=1对称时,比较f(3)、f(2)和f(2.5)的大小,需要利用对称性进行分析。 14. 求解f(x) > 1的x取值范围,需要分析0,120,-21xxxxxf在各个区间的值。 15. 根据函数0,10,3xxxxxf的图像,需要识别出哪个图像是正确表示f(x)的。 16. 已知f(x) = log_2(x),计算f(2+log_23),应用对数的性质简化计算。 以上各题涉及了函数的性质、图象、值域、零点、对称性等多个知识点,通过具体计算和分析可以解答这些问题。
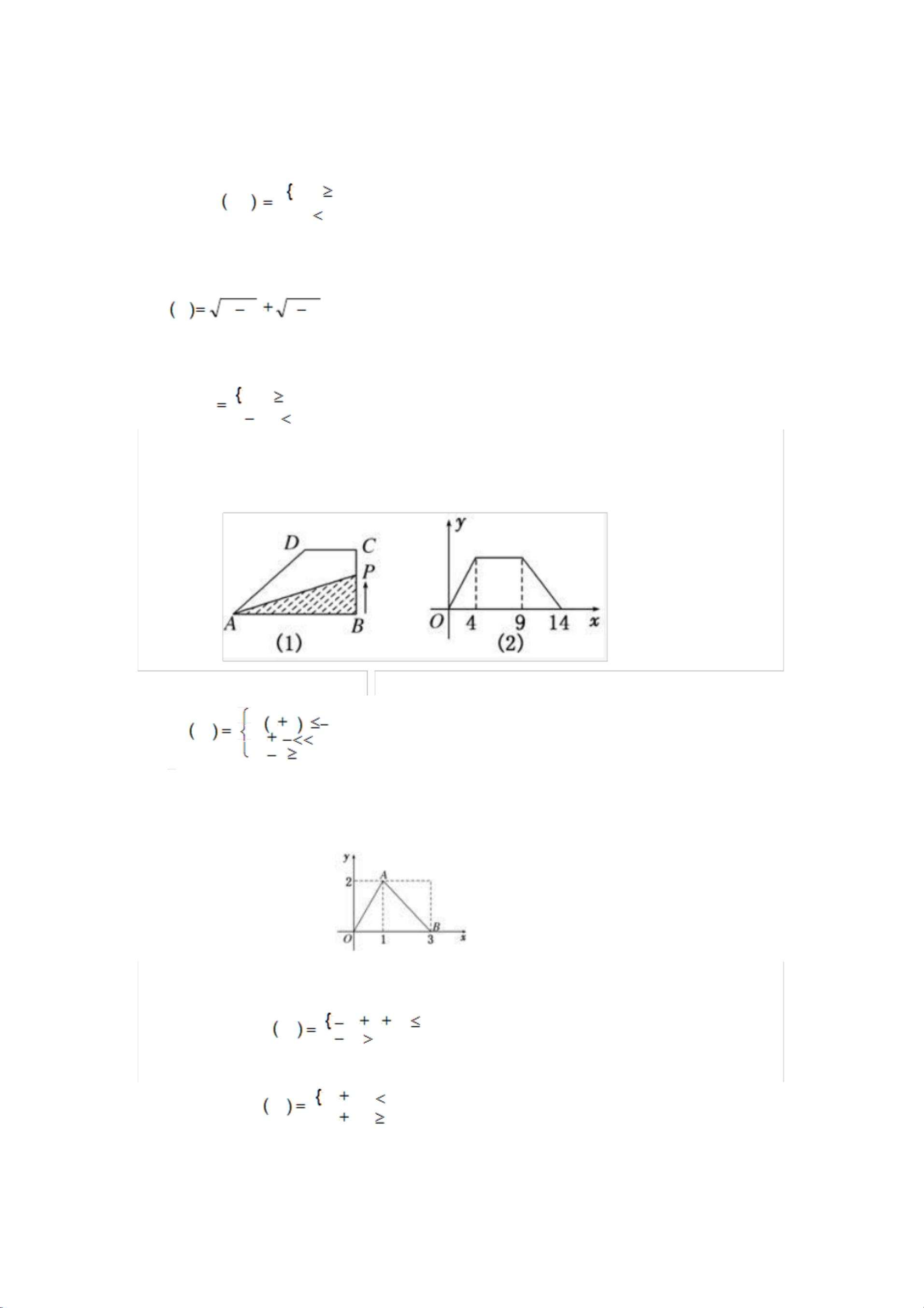

- 粉丝: 2
- 资源: 6万+




 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功