Score-based models have achieved state-of-the-art performance on many downstream tasks and applications. These tasks include, among others, image
generation (Yes, better than GANs!), audio synthesis , shape generation , and music generation . Moreover, score-based models
have connections to normalizing ow models, therefore allowing exact likelihood computation and representation learning. Additionally, modeling and estimatin
scores facilitates inverse problem solving, with applications such as image inpainting , image colorization , compressive sensing, and medical image
reconstruction (e.g., CT, MRI) .
1024 x 1024 samples generated from score-based models
This post aims to show you the motivation and intuition of score-based generative modeling, as well as its basic concepts, properties and applications.
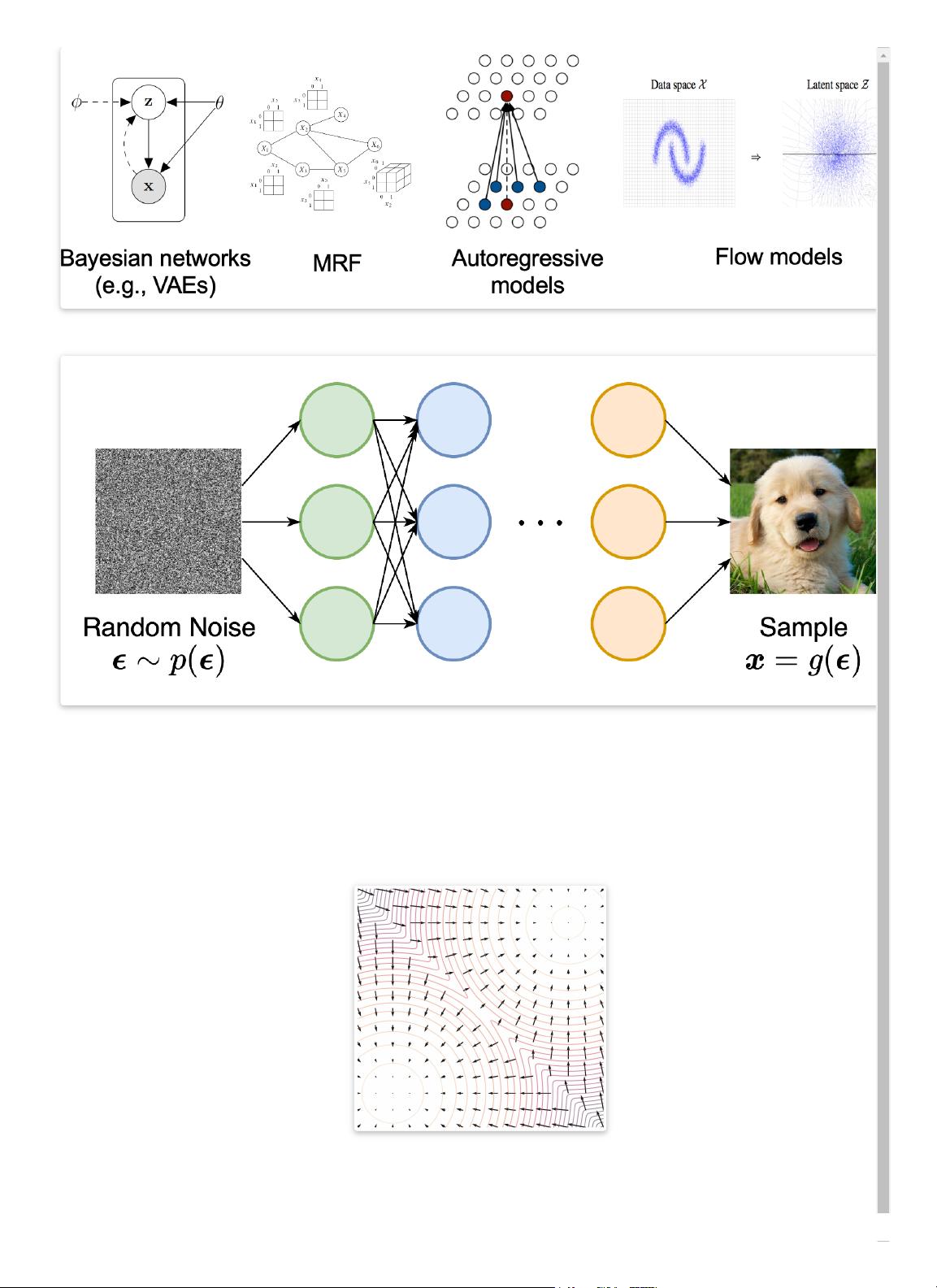
The score function, score-based models, and score matching
Suppose we are given a dataset , where each point is drawn independently from an underlying data distribution . Given this dataset, the
goal of generative modeling is to t a model to the data distribution such that we can synthesize new data points at will by sampling from the distribution.
In order to build such a generative model, we rst need a way to represent a probability distribution. One such way, as in likelihood-based models, is to directly
model the probability density function (p.d.f.) or probability mass function (p.m.f.). Let be a real-valued function parameterized by a learnable param
. We can dene a p.d.f. via
where is a normalizing constant dependent on , such that . Here the function is often called an unnormalized probabilistic mod
or energy-based model .
We can train by maximizing the log-likelihood of the data
However, equation requires to be a normalized probability density function. This is undesirable because in order to compute , we must evaluate
the normalizing constant —a typically intractable quantity for any general . Thus to make maximum likelihood training feasible, likelihood-based model
must either restrict their model architectures (e.g., causal convolutions in autoregressive models, invertible networks in normalizing ow models) to make
tractable, or approximate the normalizing constant (e.g., variational inference in VAEs, or MCMC sampling used in contrastive divergence ) which may be
computationally expensive.
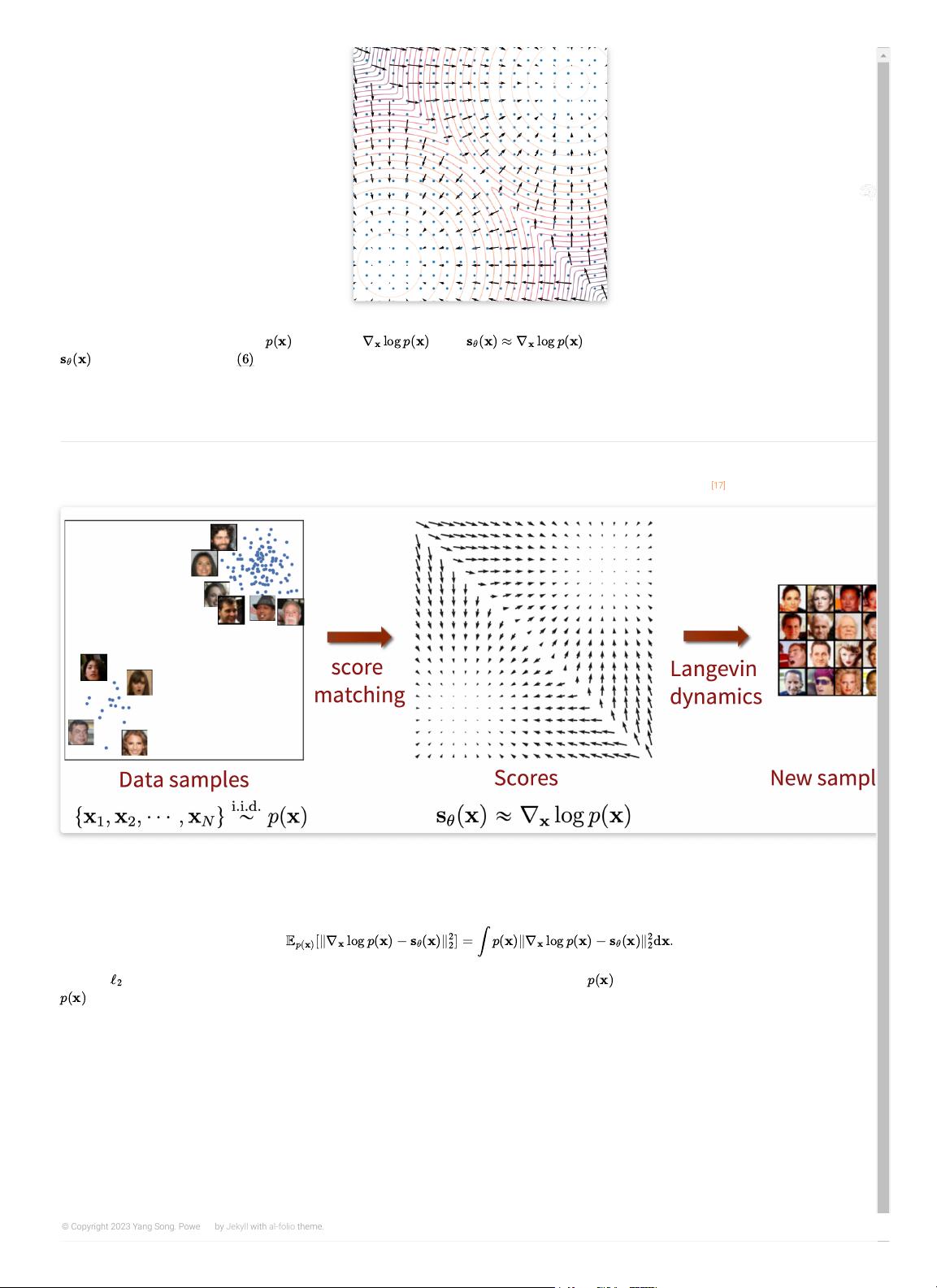
By modeling the score function instead of the density function, we can sidestep the diculty of intractable normalizing constants. The score function of a
distribution is dened as
and a model for the score function is called a score-based model , which we denote as . The score-based model is learned such that
, and can be parameterized without worrying about the normalizing constant. For example, we can easily parameterize a score-based mo
with the energy-based model dened in equation , via
[17, 18, 19, 20, 21, 22] [23, 24, 25] [26] [27]
[17, 20] [20]
[28]
[20]
{
x
1
,
x
2
, ⋯ ,
x
N
}
p
(
x
)
f
θ
(
x
) ∈
R
θ
1
p
θ
(
x
) =
e
−
f
θ
(
x
)
Z
θ
,
Z
θ
> 0
θ
∫
p
θ
(
x
)d
x
= 1
f
θ
(
x
)
[7]
p
θ
(
x
)
max
θ
N
∑
i
=1
log
p
θ
(
x
i
).
(2)
p
θ
(
x
)
p
θ
(
x
)
Z
θ
f
θ
(
x
)
Z
θ
[29]
p
(
x
)
∇
x
log
p
(
x
),
[17]
s
θ
(
x
)
s
θ
(
x
) ≈ ∇
x
log
p
(
x
)
(1)




 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助 
 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜 信息提交成功
信息提交成功

