l490 仪 器 仪 表 学 报 第 2 9卷
针对传统小波神经 网络的反向传播算法(back—prop—
agation,BP)存在着易陷人局 部极 小点和对初值要 求较
高的缺点 ,本文提出一种基 于改进算 法的小波神经 网络
算法 ,并将传统的与这种改进的小波神经 网络算法均应
用于电力变 压器故 障诊 断进行 比较研究 。大量数 据表
明,本文提 出的基于改进算法 的小波神经 网络更能对变
压器各种故障进行有效的分类 。
2 基于 BP算法的小波神经网络
小波神经网络是一种 以小波基函数为神经元激励 函
数的类人工神经网络 ,其可以看作以小波函数为基底的函
数连接型网络。本文着重研究适于故障诊断与模式识 别
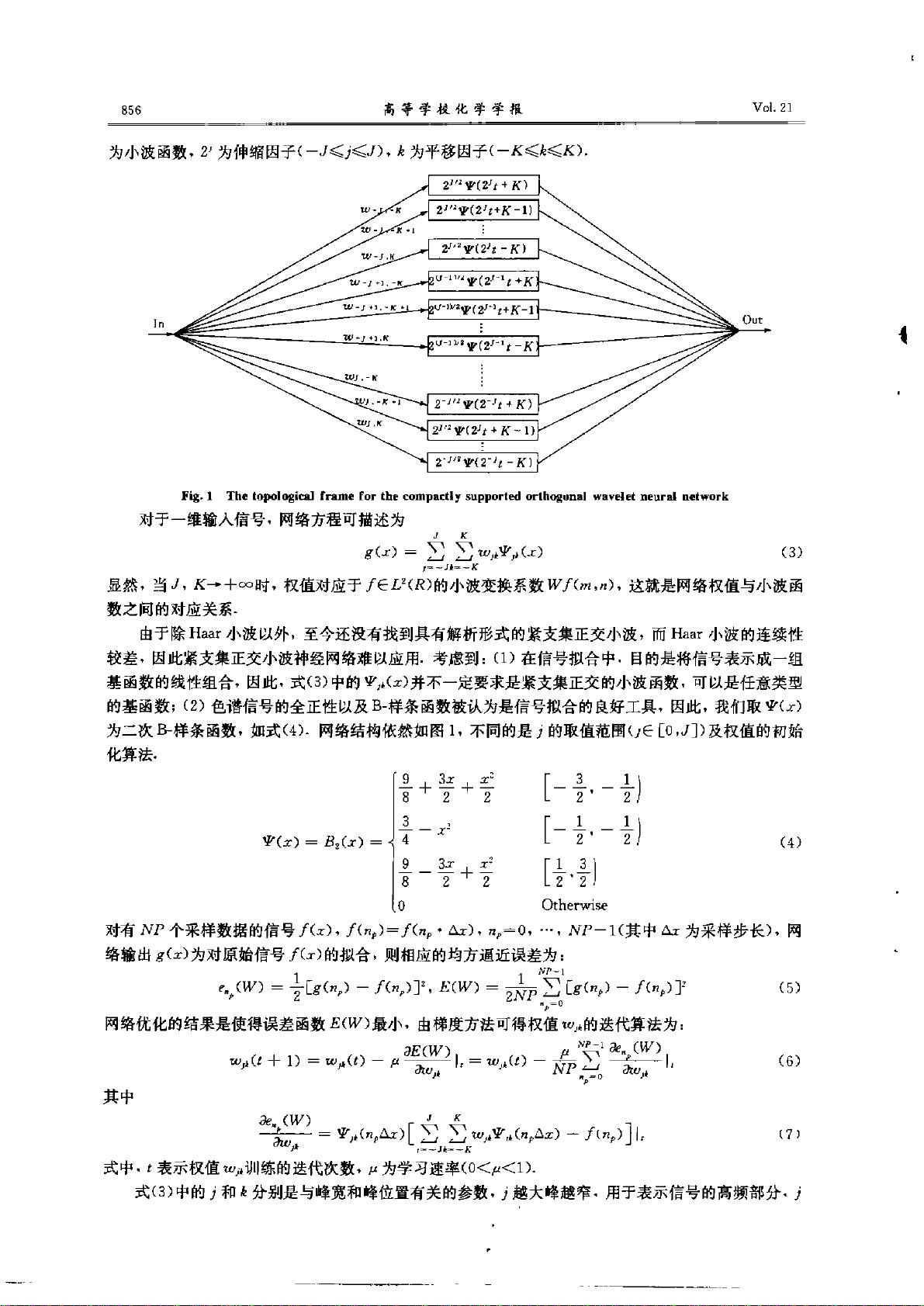
的前馈小波神经网络 ,如图 1所示为 3层前馈小波神经 网
络,包括输人层 、隐含层(小波层 和权值层组成)和输出层。
输入层 隐含层 输 出层
: 小波层 权值层 :
● ● ● ● ● ● ● ● ● ● ● ● ●
图 1小波神经 网络结构
Fig.1 Structure diagram of W NN
=
[ 。, :,…, ]是小波神经 网络 的输入量 , 为
输人层第 k个输人样本 , 为输 出层节点第 i个输 出值 ,
表示第 k个输人层节点与第 个隐含层 节点 的连接权
值 ,第 伽 表示第 j个隐含层节点与第 i个输 出节点 的连
结权值 。o,、6,分别是第 个隐含层 节点小波基的尺度参
数和平移参数 。
网络的输出可以表示为:
多 (z)= (∑ 。, [∑ (z)]) (1)
式 中:or为任意常数 。则图 1的小波神经 网络算法 可以
描述为 :网络的训练样本对为 ( ,多 ),求使误差 函数满
足误差某种精度要求 的对应 网络参数 。
· P
E= ∑ ∑ (y 一 ) (2)
小波神经网络 的学 习算法 通常采 用批处理 方式 的
BP算法(简称 BPWNN),即小波神经 网络学习过程 由正
向传播输 出过程和反向传播 调整过程组成 :在正向传播
过程 中,输人信号从输入层经隐含层逐层处理 ,直至输 出
层 ;如果在输 出层得不到期望输出,则输 出信号的误差将
沿原来 的连结通路反向传播 ,直到输人层 ,通过沿途修改
各层间的连结权值 ,使得误差达到最小 。
本文引人学 习率 卵,令小波神经 网络所有需要训练
的参数为: = { ,W ,aj,bj},则 网络参数按传统 BP算
法调整如下式 :
e(k+1)= ( )一 (3)
另外 ,可以验证 Gauss小波符合相容性条件 ,因此
本文以 Gauss小波基函数的伸缩平移系作为隐含层核 函
数构造小波神经 网络。
(t) = te (4)
3 带动量项和变学 习率的小波神经 网络
基于 BP算法的小波神经 网络训练算法 以梯度为调
节变量 ,但 是学习率 的选择 比较困难 ,大的 可 以得到
较快 的学习速率 ,但 易引起振荡 ;小 的 卵学 习稳定 ,但速
度较慢。另外 ,BP算法不能保证 收敛 到全局最小值 ,且
容易引起振荡效应 。为利用有限 的训练样本 ,本文对此
算法进行改进 ,引入带动量项和变学 习率的小波神经网
络(简称 WNN—M):
1)在 权值 调 整 中 引 人 动 量 项 ,即 (k+1) =
—玎 + △ (k)。式 中 △ (k+1)是第 k+1次迭
d仃
代计算时的修正值; (k)是前一次迭代计算时所得的
可调参数 修正值 。 为动量系数 ,动量项 △ (k)可 以
平滑梯度方 向的剧烈变化,增加算法的稳定性。
2)在网络学 习过程 中采用变学习率和最小误差保留
策略 。引人 学习率 增 加因子 和 学 习率 降低 因子 :,每
一
轮学 习结束 ,将本次误差与前次误差 比较 ,如果本次误
差较大说 明参数调整幅度过大 ,是网络振荡 ,于是本次参
数调整结果放弃 ,降低学习率和动量 因子 ,返 回前次参数
基础上重新修 正 ,直到 网络 误差脱离 振荡 ,回到下降状
态;如果本次误差较前次误差小 ,则保 留此次参数修正结
果 ,增大学习率 ,加快学习速度 。这样 ,既可以减少振荡 、
加快网络收敛速度 ,又可 以保证学习过程结束时,输 出就
是学习过程 中记录的最小误差及相应的所有可调参数。
4 小波神经网络的训练
本文对 BPWNN、WNN—M和改 良 IEC法 这 3种方
法的故障诊断性能进行 比较研究。
维普资讯 http://www.cqvip.com



















