信号与系统教学课件：Chapter 2 Linear Time-Invariant Systems.ppt

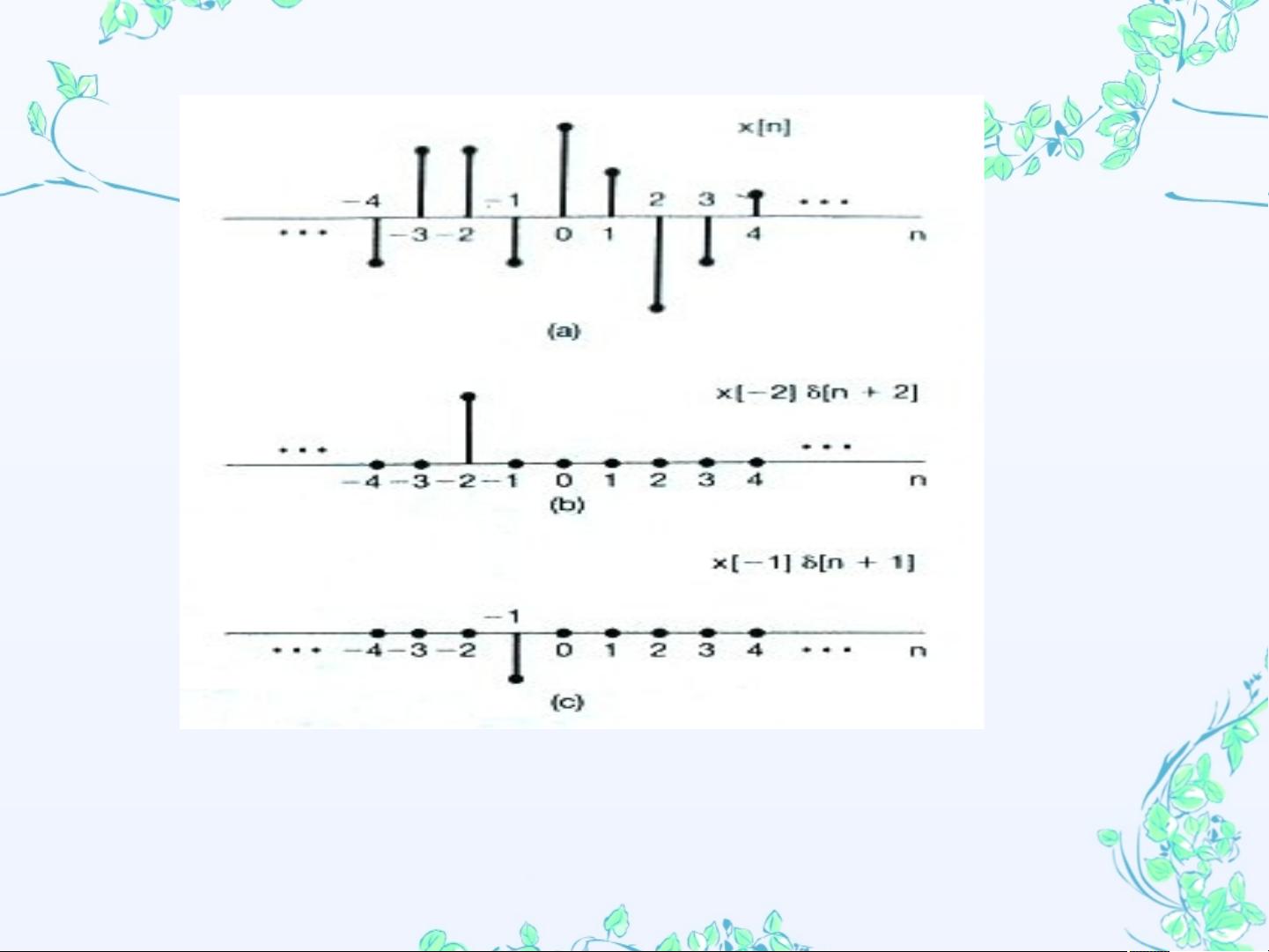
《信号与系统》是电子工程、通信工程等专业的重要课程，其核心概念之一是线性时不变系统（Linear Time-Invariant Systems，简称LTI系统）。本章主要讲解了离散时间LTI系统的卷积和（Convolution Sum）以及连续时间LTI系统的卷积积分（Convolution Integral）。 在离散时间领域，LTI系统具有两个基本特性：线性和时不变性。线性意味着系统对输入信号的加权和反应等于各输入信号分别通过系统后的反应的加权和。时不变性是指系统对任意输入信号的响应不会因为时间的平移而改变。 2.1.1 离散时间信号的脉冲表示 离散时间信号可以通过脉冲序列来表示，其中脉冲通常指单位冲激函数δ[n]。如果一个信号x[n]是单位阶跃函数u[n]，即当n >= 0时x[n] = 1，那么它可以表示为一系列的脉冲之和。 2.1.2 LTI系统的离散时间单位脉冲响应与卷积和表示 - 单位脉冲响应（Unit Impulse Response）：对于LTI系统，输入x[n]是单位冲激函数δ[n]时，系统的输出y[n]就是单位脉冲响应h[n]。 - 卷积和：LTI系统的输出y[n]可以表示为输入x[n]和单位脉冲响应h[n]的卷积和，即y[n] = x[n] * h[n]。计算卷积和时，遵循时间反转、时间平移和加权求和的规则。 方法1是一般性的计算方法，通过迭代计算每个n对应的y[n]值。方法2和方法3，特别是方法3中的多项式乘法规则，适用于处理有限长序列的卷积，因为它们可以简化计算过程。这种方法基于信号值作为多项式系数，时间点作为幂次来构造多项式，然后进行竖向乘法得到结果。 对于连续时间LTI系统，卷积积分是关键概念。2.2.1节介绍了如何将连续时间信号表示为脉冲的积分。定义δ(t)为连续时间单位冲激函数，任何连续信号可以通过与δ(t)的卷积来表示。卷积积分具有与离散时间卷积和类似的性质，但运算方式是积分而非求和。 在示例2.2.3中，给出了系统脉冲响应h[n]和输入信号x[n]，要求找到系统响应y[n]。可以采用上述三种方法中的任一方法进行求解，通过计算卷积或多项式乘法得到最终的y[n]。 总结来说，离散时间LTI系统的卷积和与连续时间LTI系统的卷积积分是理解和分析信号通过系统行为的基础工具。它们揭示了系统如何处理不同类型的输入信号，并为系统分析和设计提供了理论基础。掌握这些概念对于解决实际问题至关重要，如滤波器设计、信号处理和通信系统分析等。