胡寿松自动控制原理习题解答第二章
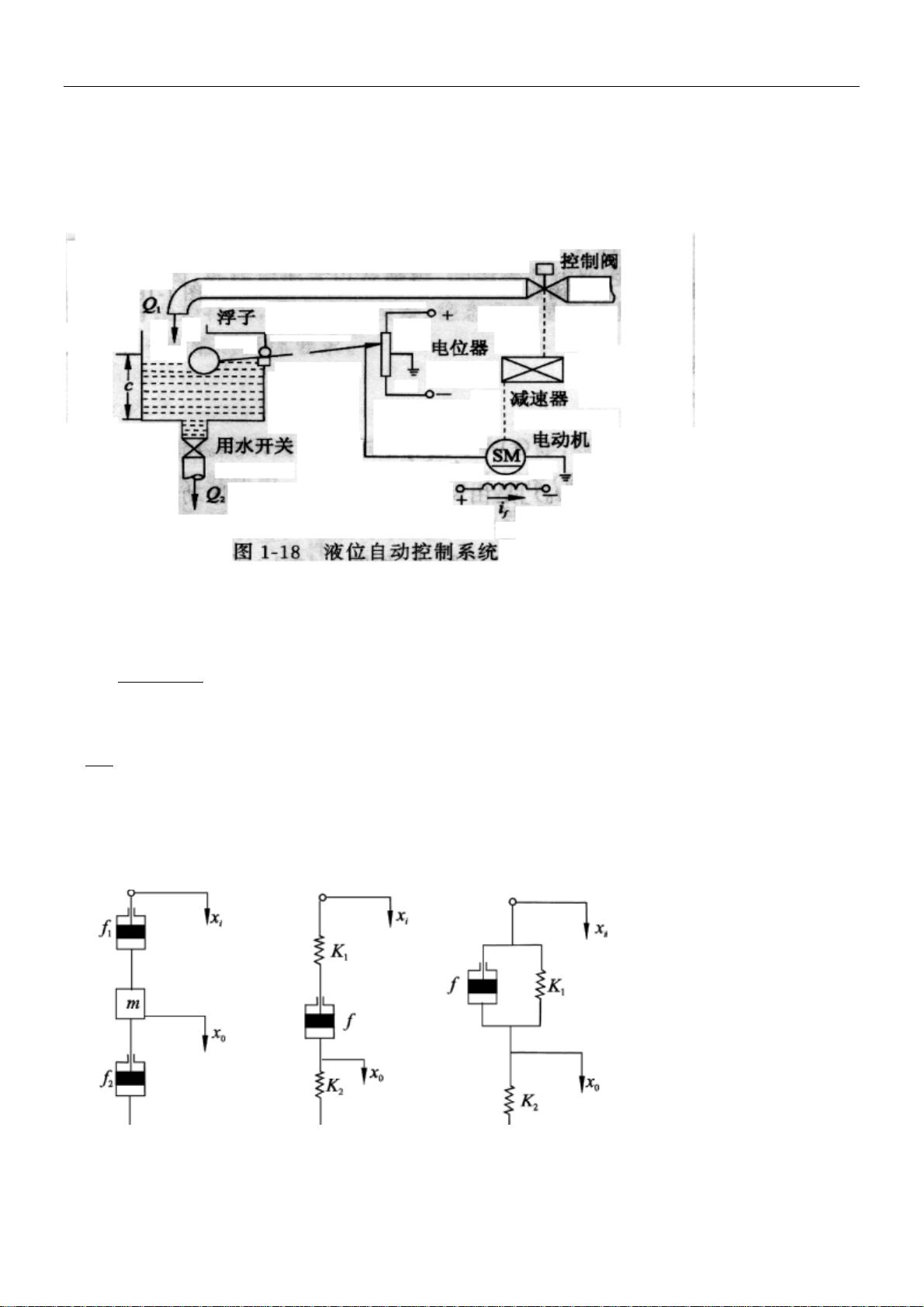
2—1 设水位自动控制系统的原理方案如图 1—18 所示,其中Q 为水箱的进水流量, 为水箱的用水流量,
1 2
Q
H
为水箱中实际水面高度。假定水箱横截面积为 F,希望水面高度 为 ,与 对应的水流量为 ,试列出
水箱的微分方程。
0
H
0
H
0
Q
解 当
Q 时,H ;当
021
QQ ==
0
H=
21
QQ
≠
时,水面高度
H
将发生变化,其变化率与流量差Q
21
Q
−
成
正比,此时有
)()(
)(
0201
0
QQQQ
dt
HHd
F −−−=
−
于是得水箱的微分方程为
21
QQ
dt
dH
F −=
2—2 设机械系统如图 2—57 所示,其中
为输入位移, 为输出位移。试分别列写各系统的微分方程式
及传递函数。
i
x
0
x
图 2—57 机械系统
解 ①图 2—57(a):由牛顿第二运动定律,在不计重力时,可得
1

胡寿松自动控制原理习题解答第二章
00201
)( xmxfxxf
i
&&&&&
=−−
整理得
dt
dx
f
dt
dx
ff
dt
xd
m
i
1
0
21
2
0
2
)( =++
将上式进行拉氏变换,并注意到运动由静止开始,即初始条件全部为零,可得
[
]
)()()(
1021
2
ssXfsXsffms
i
=++
于是传递函数为
21
1
0
)(
)(
ffms
f
sX
sX
i
++
=
②图 2—57(b):其上半部弹簧与阻尼器之间,取辅助点 A,并 设 A 点位移为
x
,方向朝下;而在其下半部工。
引出点处取为辅助点 B。则由弹簧力与阻尼力平衡的原则,从 A 和 B 两点可以分别列出如下原始方程:
)()(
01
xxfxxK
i
&&
−=−
)(
002
xxfxK
&&
−=
消去中间变量 x,可得系统微分方程
dt
dx
fKxKK
dt
dx
KKf
i
1021
0
21
)( =++
对上式取拉氏变换,并计及初始条件为零,得系统传递函数为
2121
1
0
)()(
)(
KKsKKf
sfK
sX
sX
i
++
=
③图 2—57(c):以
的引出点作为辅助点,根据力的平衡原则,可列出如下原始方程:
0
x
0201
)()( xKxxfxxK
ii
=−+−
&&
移项整理得系统微分方程
i
i
xK
dt
dx
fxKK
dt
dx
f
1021
0
)( +=++
对上式进行拉氏变换,并注意到运动由静止开始,即
0)0()0(
0
== xx
i
则系统传递函数为
)()(
)(
21
1
0
KKfs
Kfs
sX
sX
i
++
+
=
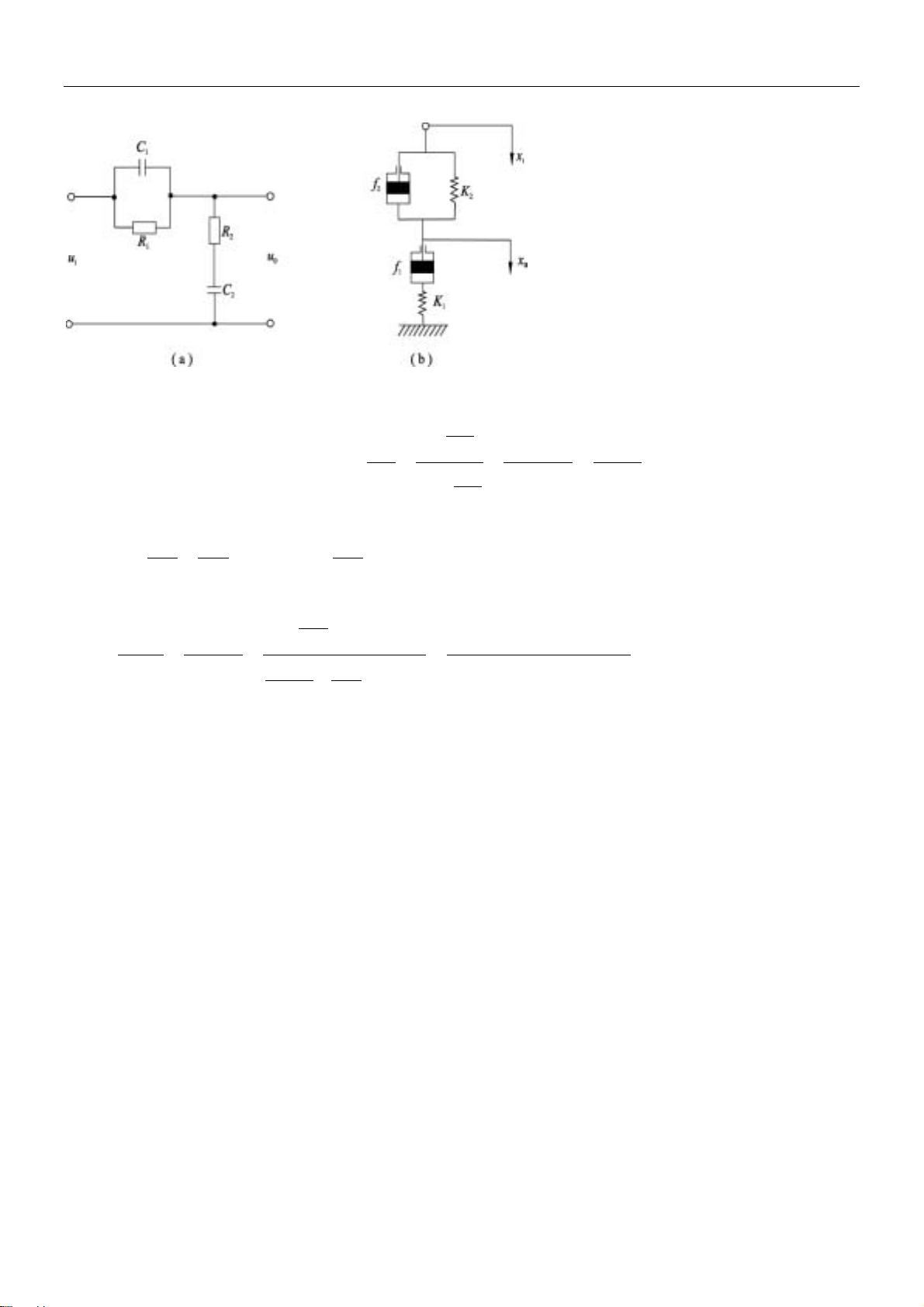
2-3 试证明图2-58(a)的电网络与(b)的机械系统有相同的数学模型。
2
胡寿松自动控制原理习题解答第二章
图 2-58 电网络与机械系统
解:(a):利用运算阻抗法得:
11
1
1
1
//
1
1
11
1
1
1
1
1
1
11
+
=
+
=
+
==
sT
R
sCR
R
sC
R
sC
R
sC
RZ
()()
1
1
1
11
2
2
22
22
22
+=+=+= sT
sC
sCR
sCsC
RZ
所以:
)1)(1(
)1)(1(
)1(
1
1
)1(
1
)(
)(
2121
21
2
21
1
2
2
21
2
0
+++
++
=
++
+
+
=
+
=
sTsTsCR
sTsT
sT
sCsT
R
sT
sC
ZZ
Z
sU
sU
i
(b)以
和 之间取辅助点 A,并设 A 点位移为
1
K
1
f
x
,方向朝下;根据力的平衡原则,可列出如下原始方程:
)()()(
010202
xxfxxfxxK
ii
&&&&
−=−+− (1)
)(
011
xxfxK
&&
−= (2)
所以
(3) xKxxfxxK
ii 10202
)()( =−+−
&&
对(3)式两边取微分得
xKxxfxxK
ii
&&&&&&&
10202
)()( =−+− (4)
将(4)式代入(1)式中得
)()()()(
021021011021021
xxffxxKfxfKxxfKxxKK
iiii
&&&&&&&&&
−
−
−
−=−+−
整理上式得
iiii
xKKxfKxKfxff
xKKxfKxfKxKfxff
21212121
021021011021021
+++=
++++
&&&&
&&&&&
对上式去拉氏变换得
3
胡寿松自动控制原理习题解答第二章
[
]
[]
)()(
)()(
212121
2
21
021211121
2
21
sXKKsfKKfsff
sXKKsfKfKKfsff
i
+++=
++++
所以:
2
1
2
21
2
21
2
1
2
21
2
21
21
2
21
2
21
21
21211121
2
21
212121
2
21
0
)1)(1(
)1)(1(
1)(
1)(
)(
)(
)(
)(
1
1
1
1
K
f
s
K
f
s
K
f
s
K
f
s
K
f
K
f
s
K
f
K
f
s
KK
ff
s
K
f
K
f
s
KK
ff
KKsfKfKKfsff
KKsfKKfsff
sX
sX
i
+++
++
=
++++
+++
=
++++
+++
=
所以
图 2-58(a)的电网络与(b)的机械系统有相同的数学模型。
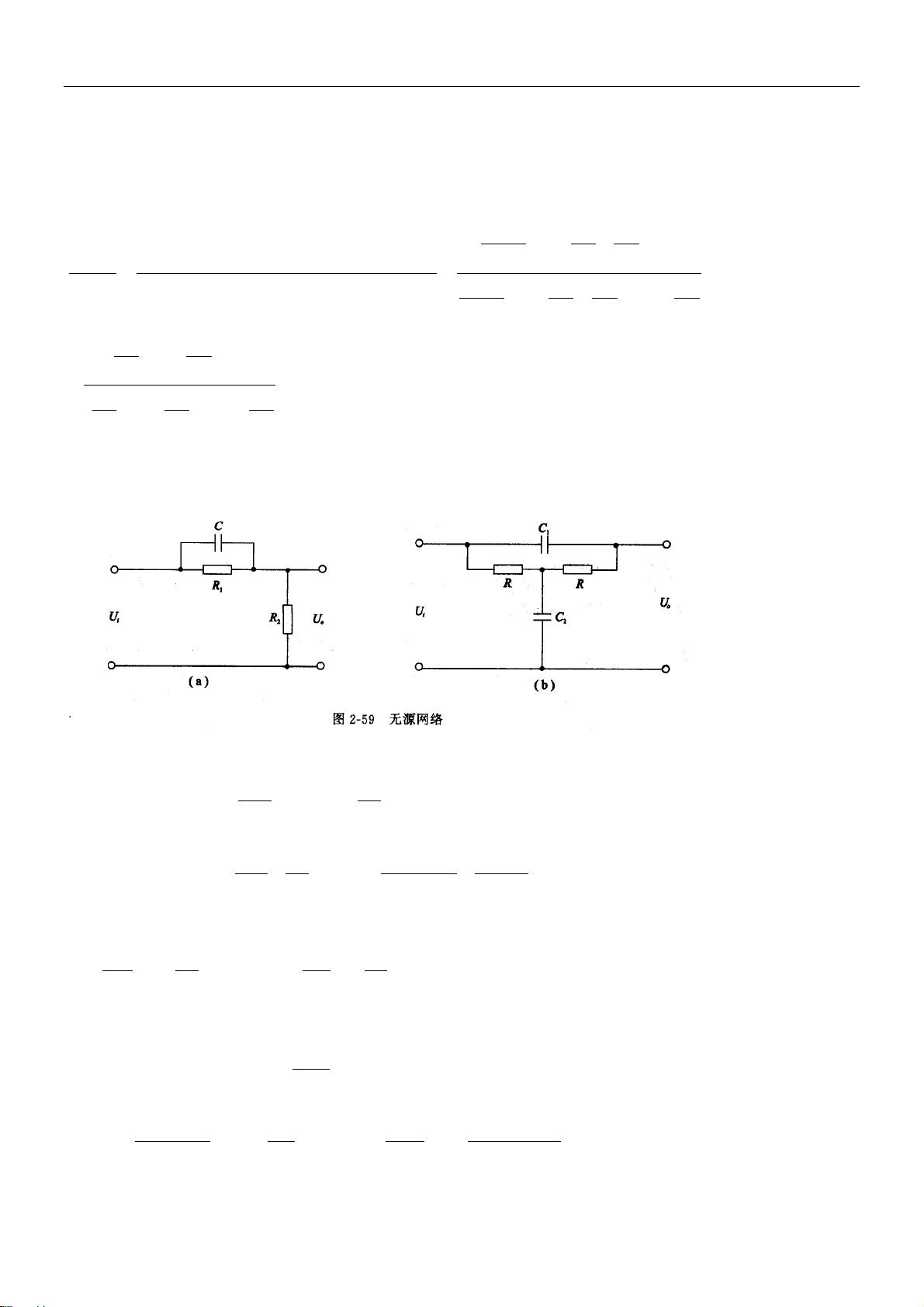
2—4 试分别列写图 2-59 中个无源网络的微分方程式。
解:(a) :列写电压平衡方程:
Ci
uuu =−
0
dt
du
C
C
C
=
i
1
1
R
u
i
C
R
=
(
)
2
1
00
2
1
210
)( R
R
uu
dt
uud
CR
R
u
dt
du
CRiiu
iiCC
RC
−
+
−
=
+=+=
整理得:
i
i
u
R
R
C
dt
du
CRu
R
R
C
dt
du
CR
1
2
20
1
2
0
2
1 +=
++
(b) :列写电压平衡方程:
10 Ci
uuu =− (1)
dt
du
Ci
C
C
1
11
= (2)
dt
Riud
C
dt
du
Ci
R
u
i
R
Riu
CC
C
C
C
CC
C
)(
2
10
2
2
21
1
1
11
2
i
−
==+=+
+
= (3)
4

胡寿松自动控制原理习题解答第二章
即:
dt
Riud
Ci
R
u
C
C
C
)(
2
10
21
1
−
=+
(4)
将(1)(2)代入(4)得:
2
1
2
21
0
2
0
1
0
)(
2
dt
ud
RCC
dt
du
C
dt
uud
C
R
uu
Cii
−=
−
+
−
即:
2
0
2
21
2
2
21
0
2
0
11
0
22
dt
ud
RCC
dt
ud
RCC
dt
du
C
dt
du
C
dt
du
C
R
u
R
u
iii
+−=−+−
整理得:
dt
du
C
R
u
dt
ud
RCC
R
u
dt
du
CC
dt
ud
RCC
iii
1
2
2
21
00
12
2
0
2
21
2)2( ++=+++
2-5 设初始条件均为零,试用拉氏变换法求解下列微分方程式,并概略绘制x(t)曲线,指出各方程式的模态。
(1)
;)()(2 ttxtx =+
&
解:对上式两边去拉氏变换得:
(2s+1)X(s)=1/s
2
→
12
411
)12(
1
)(
22
+
+−=
+
=
ss
sss
sX
运动模态
t
e
5.0−
所以:
)1(2)(
2
1
t
ettx
−
−−=
(2)
)。ttxtxtx ()()()(
δ
=++
&&&
解:对上式两边去拉氏变换得:
1)()1(
2
=++ sXss →
4/3)2/1(
1
)1(
1
)(
22
++
=
++
=
sss
sX
运动模态
−
te
t
2
3
sin
2/
所以:
=
−
tetx
t
2
3
sin
3
2
)(
2/
(3)
)。ttxtxtx (1)()(2)(
=
++
&&&
解:对上式两边去拉氏变换得:
s
sXss
1
)()12(
2
=++ →
222
)1(
1
1
11
)1(
1
)12(
1
)(
+
+
+
−=
+
=
++
=
s
ss
sssss
sX
5

















