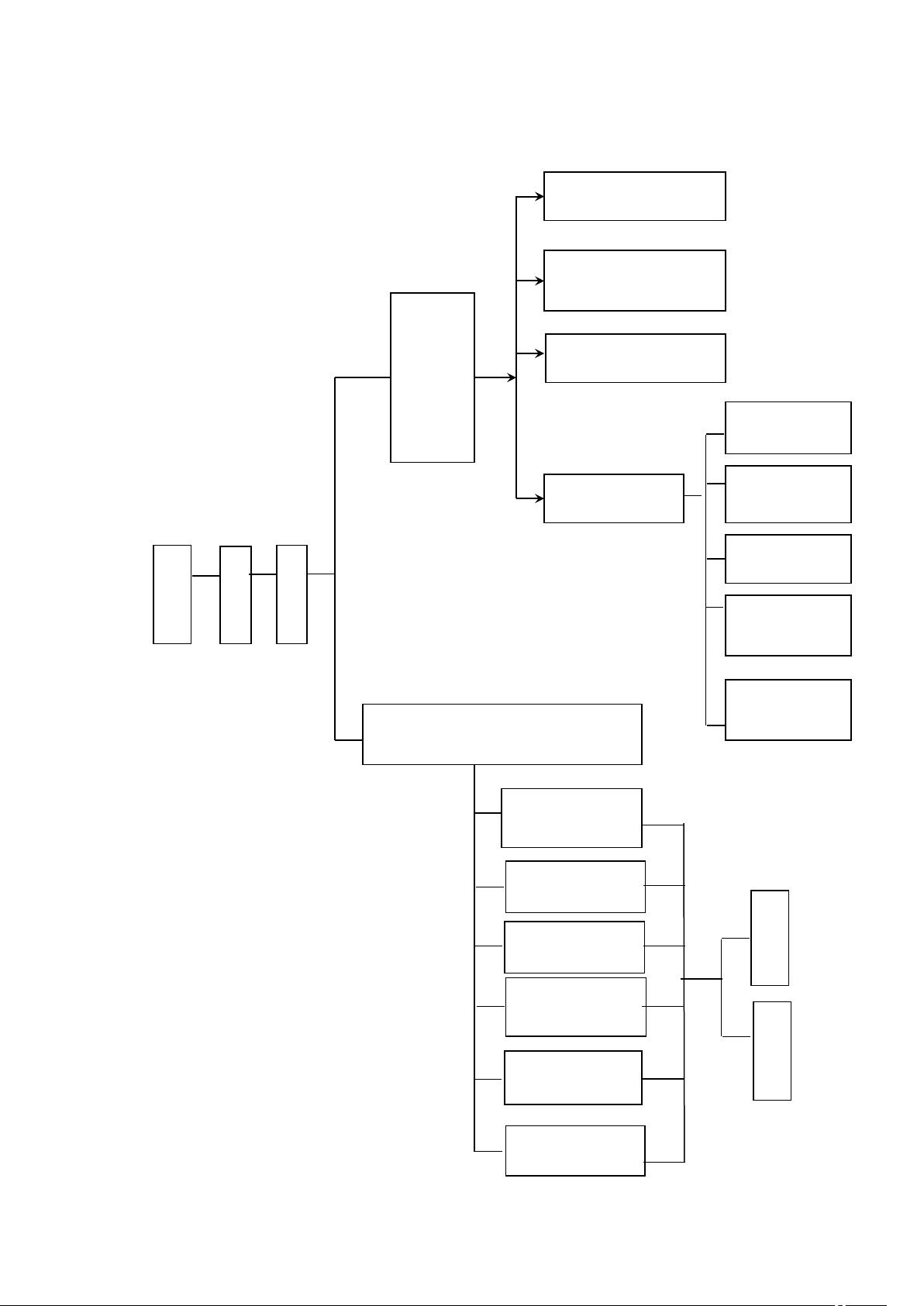
在数学和计算机科学中,函数是至关重要的概念,它们构成了我们理解和解决问题的基础。"函数章节知识树.doc" 文件显然提供了一个全面的框架,用于学习和理解函数的各种方面。以下是根据提供的部分内容,对函数相关知识的详细说明:
1. **函数的概念**:
函数是一种规则,它将一个集合(称为定义域)中的每个元素与另一个集合(称为值域)中的唯一元素关联起来。这种对应关系可以用数学表达式或图示法表示。函数的表示通常为 f(x),其中 x 是自变量,f(x) 是对应的因变量。
2. **函数的符号**:
函数符号 f(x) 表示一个函数,其中 f 是函数名,x 是输入,f(x) 是输出。例如,f(x) = x^2 是一个二次函数,其中 f(x) 是 x 的平方。
3. **函数的图像**:
函数的图像通常是在笛卡尔坐标系中绘制的曲线,通过这个图像我们可以直观地看出函数的形状、增减性以及可能的极值。例如,正比例函数(如 f(x) = kx)是一条通过原点的直线,而二次函数(如 f(x) = ax^2 + bx + c)则呈现“U”形或倒“U”形。
4. **函数的性质**:
- **定义域**:函数可以接受的所有可能输入的集合。
- **值域**:函数可能产生的所有输出的集合。
- **奇偶性**:如果 f(-x) = f(x),那么函数是偶函数;如果 f(-x) = -f(x),则为奇函数。
- **单调性**:如果函数在某个区间内,随着自变量增加,函数值也增加,那么它是增函数;反之,如果函数值随着自变量增加而减少,则是减函数。
- **周期性**:如果存在一个非零常数 T,使得 f(x+T) = f(x) 对所有 x 成立,那么函数是周期函数,T 是其周期。
5. **函数的一般知识**:
这涵盖了函数的基本概念和理论,包括函数的组合、复合函数、反函数以及函数的逆运算。
6. **正比例函数**:
正比例函数 f(x) = kx,其中 k 是常数,其图像是一条穿过原点的直线,斜率为 k。
7. **反比例函数**:
反比例函数 f(x) = 1/x,其图像在第一和第三象限形成两个分支,且无限接近但永不触及坐标轴。
8. **一次函数**:
一般形式为 f(x) = mx + b,其中 m 和 b 是常数,m 是斜率,b 是 y 轴截距。
9. **二次函数**:
二次函数 f(x) = ax^2 + bx + c,其中 a、b 和 c 是常数,a ≠ 0。其图像是一个抛物线,开口方向取决于 a 的正负。
10. **对数函数**:
对数函数 f(x) = log_b x,其中 b 是基数,x > 0,其逆函数是指数函数。
11. **指数函数**:
指数函数 f(x) = a^x,其中 a 是底数,a > 0 且 a ≠ 1,其图像根据 a 的大小表现出不同的增长或衰减特性。
这些基本的初等函数是数学和计算机科学中的基础,它们在各种领域都有应用,如物理学、工程学、经济学和数据分析。深入理解和掌握这些函数的性质和图像,对于解决实际问题和进一步学习高级数学概念至关重要。