
附录 1
华南农业大学信息学院
课程设计
姓名:
学号:
班级:
课程名称:数据结构
任课教师:杨秋妹
1
附录 2 华南农业大学信息学院
数据结构课程设计完成情况登记表
起止日期:20109.3--2010.6
专业班级 学号 姓名 完成日期
设
计
完
成
情
况
记
录
题 目 名 称
算法设计 独立完成情况 测试情况 是否书
写报告
并提交
成功 失败 独立 帮助 提交
情况
提交
时间
北大
系统
团队实验(此处填写完成的排
序方法)
(此处填写通过 与 不
通过,及完成周 数 ,
如通过,第 2 周)
图的遍历——深度优先 Poj1979
图的遍历——广度优先 Poj1915
拓扑排序 Poj1094
最小生成树 Poj1251
最短路径 Poj1125
拓展实验(平衡二叉树)
√ √
通过,第九周 是
自
我
评
价
成
绩
A 完成基础实验要求的全部功能并运行通过,拓展一类部分完成良好。算法有一
定的新意,程序代码符合书写规范,实验报告叙述清晰完整,有详尽的分析和总结。
B 完成基础实验要求的全部功能,拓展一类部分完成良好。程序代码符合书写规
实验报告叙述清晰完整。
C 完成并运行实验要求的大部分功能,实验报告良好。
D 仅完成并运行实验要求的部分功能。
E 未按时完成实验,或者抄袭。
2
指导教师:杨秋妹
一、实验内容
1, 利用平衡二叉树实现一个动态查找表,实现动态查找表的三种基本功能:查找,插
入、删除和附加的两种功能:合并、分裂平衡二叉树。
2, 操作界面要给创建、查找、插入、删除、合并和分裂六种操作供选择。每种操作均
要提示输入关键字。每次插入和删除一个节点后,应更新平衡二叉树的显示。该二
叉树的显示采用凹入表形式。
二、实验思路分析
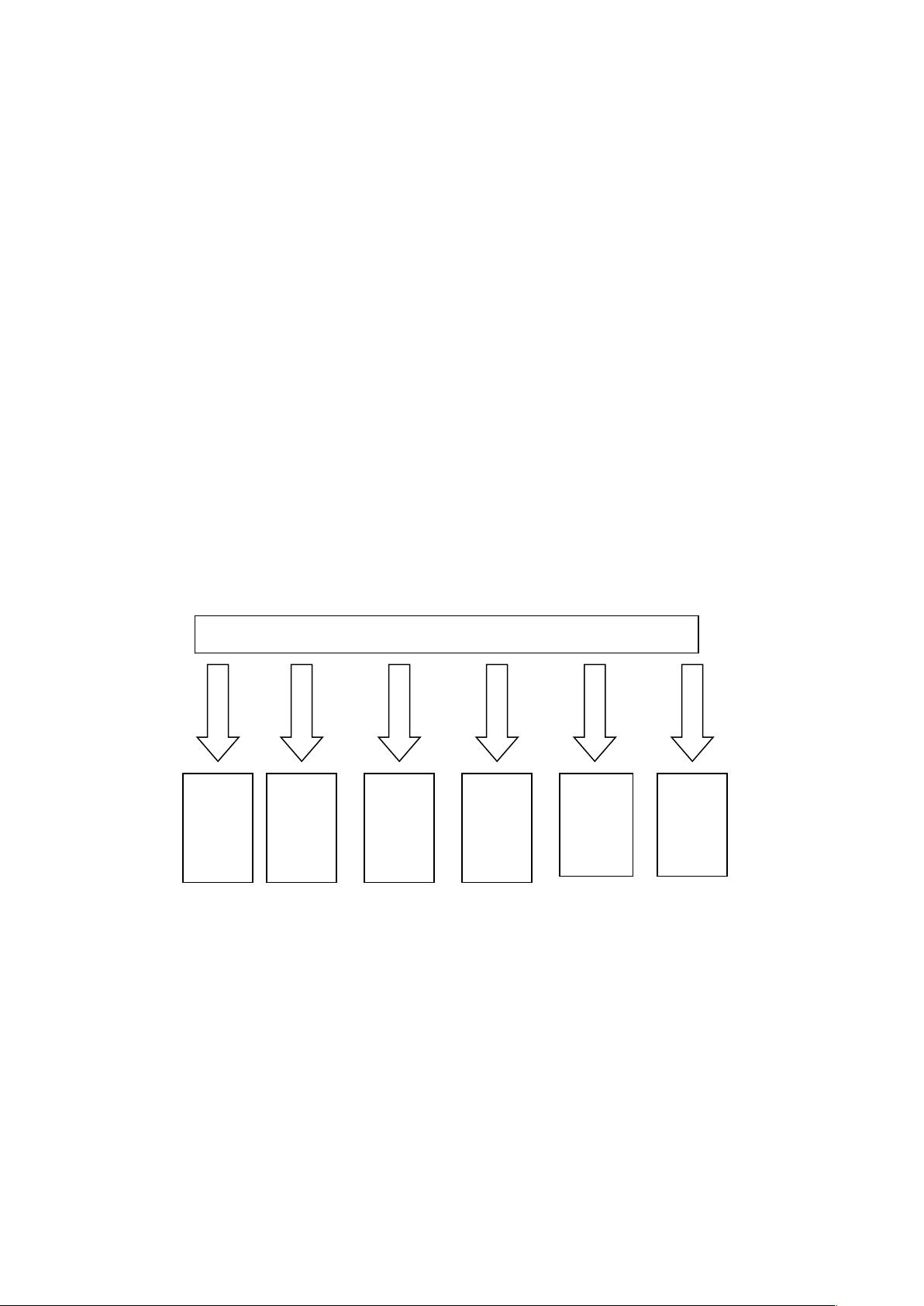
本程序共分七大模块:(1)程序主函数;(2)平衡二叉树的初始化;(3)平衡二叉
树的插入;(4)平衡二叉树的查找;(5)平衡二叉树的删除;(6)平衡二叉树的的合并;
(7)平衡二叉树的分裂。
函数简单关系图:
三、算法设计
1、平衡二叉树的存储表示
#include<stdio.h>
#include<stdlib.h>
#include<iostream.h>
#include<string.h>
#define TRUE 1
#define FALSE 0
初
始
化
插
入
查
找
删
除
合
并
分
裂
3
主程序模块

#define LH +1 //左高
#define RH -1 //右高
#define EH 0 //等高
typedef struct ElemType{
int key;
}ElemType;
typedef struct BSTNode{
ElemType data;
int bf; //结点的平衡因子
struct BSTNode *lchild,*rchild; //左右孩子指针
}BSTNode,*BSTree;
2、算法描述
:
Status InserAVL( &T, key,taller)
//若 T 不存在和 key 有相同关键字的节点,则插入一个数据元素为 key 的新节点,
//返回 1,否则返回 0,若因插入而使 T 失去平衡,则作平衡旋转处理,taller 反映
//树长高与否。
BSTree CreateBiTree &T)
//输入各结点的 key ,以'#'表示输入结束
Void DispTree (T, i, j)
//以凹入表的形式输出 T 树,附带各结点的平衡因子。
void DeleteNode (&T, e)
//若 key 存在就删除该值,若因删除而使 T 失去平衡,而做//平衡旋转处理。
void Merge_T (BSTree &T1,BSTree &T2)
//把 T2 合并到 T1 上,重新使 T1 成为平衡二叉树。
void Devide_T (&T, &T1)
//把 T 以 flag 为分界线。使 T 的值都大于 flag,T1 的值小于或等于 falg。
Void R_Rotate(&T)
//对以 T 为根的二叉排序树做右旋处理,处理之后 T 指向新的树根节点,即旋转处
理//之前的左子树的根节点。
Void L_Rotate(&T)
//对以 T 为根的二叉排序树做左旋处理,处理之后 T 指向新的树根节点,即旋转处
理
//之前的右子树的根节点。
4

Void LeftBalance(&T)
//对以 T 所指节点为根的二叉树做左平衡旋转处理,最后 T 指向新的根节点。
Void RightBalance(&T)
//对以 T 所指节点为根的二叉树做右平衡旋转处理,最后 T 指向新的根节点。
Status Search( T, e)
//查找 T 中是否存在结点 e,找到则返回该值的节点,否则返回 NULL。
四、编程实现:
功能函数:
void DispTree(BSTree T,int i,int j){ //树的打印输出
if(T->rchild)
DispTree(T->rchild,i+4,j);
for(j=1;j<=i;j++) printf(" ");
printf("%d",T->data.key);
printf("("); printf("%d",T->bf); printf(")");
printf("\n");
if(T->lchild)
DispTree(T->lchild,i+4,j);
}
void R_Rotate(BSTree &p) {
// 对以*p 为根的二叉排序树作右旋处理,处理之后 p 指向新的树根结点,即旋转处理之
前的左子树的根结点
BSTree lc;
lc = p->lchild; // lc 指向*p 的左子树根结点
p->lchild = lc->rchild; // lc 的右子树挂接为*p 的左子树
lc->rchild = p; p = lc; // p 指向新的根结点
}
void L_Rotate(BSTree &p) {
// 对以 p↑为根的二叉排序树作左旋处理,处理之后 p 指向新的树根结点,即旋转处理之
前的右子树的根结点
BSTree rc;
rc = p->rchild; // rc 指向*p 的右子树根结点
p->rchild = rc->lchild; // rc 的左子树挂接为*p 的右子树
rc->lchild = p; p = rc; // p 指向新的根结点
}
void RightBalance(BSTree &T) {
// 对以指针 T 所指结点为根的二叉树作右平衡旋转处理, 本算法结束时,指针 T 指向
5


















