选址问题 matlab lingo

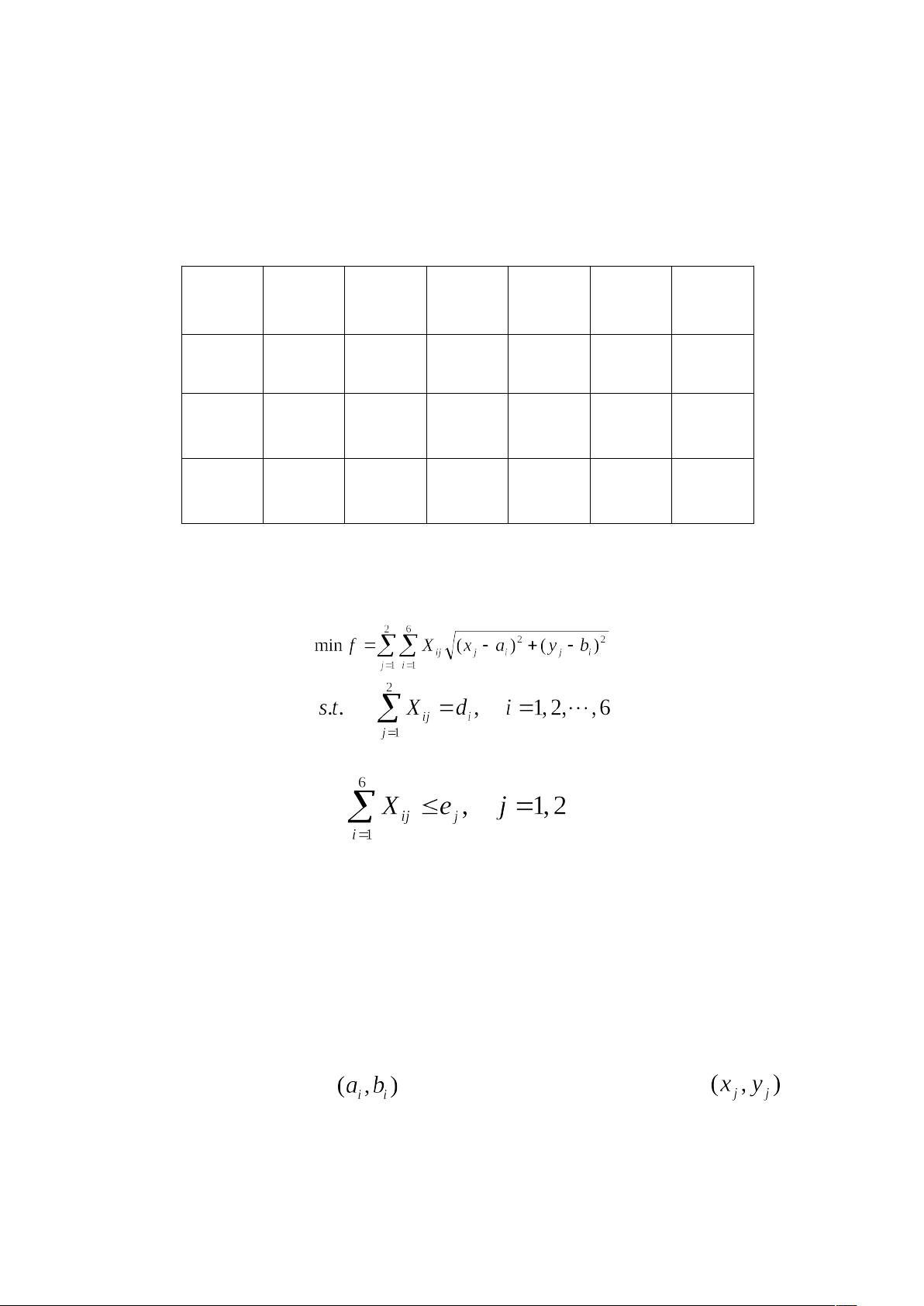
某公司有6个建筑工地要开工，每个工地的位置（用平面坐标系 表示，距离单位：千米 ）及水泥日用量 (吨)由下表给出。目前有两个临时料场位于A(5,1)，B(2,7)，日储量各有20吨。假设从料场到工地之间均有直线道路相连。 问题（1）：试制定每天的供应计划，即从A，B两料场分别向各工地运送多少吨水泥，使总的吨千米数最小； 问题（2）：为了进一步减少吨千米数，打算舍弃两个临时料场，改建两个新的，日储量各为20吨，问应建在何处，节省的吨千米数有多大？ 该问题涉及数学建模、线性规划以及使用MATLAB和LINGO软件进行求解。具体来说，这是一个选址问题，目标是优化物流运输成本，降低总的吨千米数。 问题一的模型是一个线性规划问题，目的是确定从两个现有料场A和B向六个建筑工地运输水泥的最优策略。每个工地的需求量、料场的位置以及它们之间的距离已知。MATLAB代码通过构建目标函数系数向量`CC`（表示吨千米数）和约束矩阵，包括不等式约束（料场储量限制）和等式约束（工地需求量），然后使用`linprog`函数寻找最小化吨千米数的解。 问题二则更复杂，因为它不仅需要优化运输计划，还要确定新建料场的位置。这引入了额外的决策变量（新料场的坐标），使得问题变为一个非线性规划问题。MATLAB代码的修改之处在于添加了新的变量和相应的约束，同时可能需要使用非线性规划求解器，如`fmincon`，因为料场的位置不再是固定的。 LINGO是另一种用于解决这类优化问题的软件，它具有内置的建模语言，可以更直观地表达问题。在LINGO中，模型可能会类似下面的形式： ```lingo sets: sites/1..6/:d, x, y; yards/1..2/:e, x, y; param: a1..6 = {sites}1.25, 8.75, 0.5, 5.75, 3, 7.25; b1..6 = {sites}1.25, 0.75, 4.75, 5, 6.5, 7.75; d1..6 = {sites}3, 5, 4, 7, 6, 11; x1..2 = {yards}5, 2; y1..2 = {yards}1, 7; e1..2 = {yards}20, 20; var: X1..61..2 >= 0; ! 从料场到工地的运输量 minimize: sum{(sites, yards): sqrt((x[j] - a[i])^2 + (y[j] - b[i])^2) * X[i,j]} + sum{(yards, sites): sqrt((x[j] - a[i])^2 + (y[j] - b[i])^2) * X[i,j]}; subject to: sum{yards: X[i,j]} = d[i], forall sites(i); sum{(sites, yards): X[i,j]} + sum{(yards, sites): X[i,j]} <= e[j], forall yards(j); ! 问题二的新料场位置变量和约束 var: x3, y3, x4, y4 >= 0; ! 新料场坐标 minimize: old_cost + new_cost - (sum{(sites, yards): sqrt((x[j] - a[i])^2 + (y[j] - b[i])^2) * X[i,j]} + sum{(yards, sites): sqrt((x[j] - a[i])^2 + (y[j] - b[i])^2) * X[i,j]}) - (sum{(sites, yards): sqrt((x3 - a[i])^2 + (y3 - b[i])^2) * X[i,3]} + sum{(yards, sites): sqrt((x3 - a[i])^2 + (y3 - b[i])^2) * X[i,3]} - (sum{(sites, yards): sqrt((x4 - a[i])^2 + (y4 - b[i])^2) * X[i,4]} + sum{(yards, sites): sqrt((x4 - a[i])^2 + (y4 - b[i])^2) * X[i,4]}); subject to: ... ! 相关的约束，如新料场储量和需求量的满足 ``` 在这个LINGO模型中，我们增加了新料场的坐标变量，并重新构造了目标函数，以便比较旧方案和新方案的吨千米数。注意，完整的LINGO模型还需要包含新料场的约束，比如存储量和所有工地的供需平衡。 通过MATLAB或LINGO运行这两个模型，可以得到最优化的运输计划和新料场的最佳位置，从而降低总的吨千米数，实现物流成本的最小化。这种选址和运输问题在物流、供应链管理和设施布局等领域有着广泛的应用。