Surveyofmaneuveringtargettracking:II.Ballistictargetmodels资源-CSDN文库

目标追踪

需积分: 21 135 浏览量 2019-11-26 15:08:42 上传评论收藏 274KB PDF 举报

资源推荐

资源详情

资源评论

PROCEEDINGS OF SPIE

SPIEDigitalLibrary.org/conference-proceedings-of-spie

Survey of maneuvering target

tracking: II. Ballistic target models

X. Rong Li, Vesselin P. Jilkov

X. Rong Li, Vesselin P. Jilkov, "Survey of maneuvering target tracking: II.

Ballistic target models," Proc. SPIE 4473, Signal and Data Processing of

Small Targets 2001, (26 November 2001); doi: 10.1117/12.492753

Event: International Symposium on Optical Science and Technology, 2001,

San Diego, CA, United States

Downloaded From: https://www.spiedigitallibrary.org/conference-proceedings-of-spie on 24 Nov 2019 Terms of Use: https://www.spiedigitallibrary.org/terms-of-use

A Survey of Maneuvering Target Tracking—Part II: Ballistic Target Models



X. Rong Li and Vesselin P. Jilkov

Department of Electrical Engineering

University of New Orleans

New Orleans, LA 70148, USA

504-280-7416, -3950 (fax), xli@uno.edu, vjilkov@uno.edu

Abstract

This paper is the second part in a series that provides a comprehensive survey of the problems and techniques of tracking

maneuvering targets in the absence of the so-called measurement-origin uncertainty. It surveys motion models of ballistic

targets used for target tracking. Models for all three phases (i.e., boost, coast, and reentry) of motion are covered.

Key Words: Target Tracking, Maneuvering Target, Dynamics Model, Ballistic Target, Survey

1 Introduction

A survey of dynamics models used in maneuvering target tracking has been reported in [1]. It, however, does not cover

motion models used for tracking ballistic targets (BT), that is, ballistic missiles, decoys, debris, and satellites. The primary

reason for this omission is that these models possess many distinctive features that differ vastly from those covered in [1]. To

supplement [1], a survey of these models is presented in this paper. To our knowledge, such a survey is not available in the

literature. Measurement models are surveyed in Part III [2].

The entire trajectory of a BT, from launch to impact, is commonly divided into three basic phases [3, 4]: boost

, ballistic

(also known as coast), and reentry. The boost phase of motion is the powered, endo-atmospheric ﬂight, which lasts from

launch to thrust cutoff or burnout. It is followed by the ballistic phase, which is an exo-atmospheric, free-ﬂight motion,

continuing until the Earth’s atmosphere is reached again. The atmospheric reentry begins when the atmospheric drag becomes

considerable and endures until impact.

Target dynamics during the different phases are substantially different. A succinct ouline of the main dynamic phases

is given in [5]. The boost phase is characterized by a large (primarily axial) thrust acceleration, which in the case of rocket

staging is subject to abrupt, jump-wise changes. The effects of the atmospheric drag and the Earth’s gravity are also essential

in this phase. After the boost (i.e., during the post-boost), drag is no longer present and the level of thrust becomes low

or vanishes. During the exo-atmospheric ballistic phase the motion is governed essentially by the Earth’s gravity only —

the trajectory is more predictable, still, small re-targeting maneuvers are possible. The reentry phase features a rapid drag

deceleration with possible lateral accelerations.

Overall, a ballistic target has a less uncertain motion than many other types of powered vehicles, such as maneuveringair-

craft or agile missiles: Most BTs follow a ﬂight path that is to a large extent predetermined by the performancecharacteristics,

speciﬁc for a target type, hence the name ballistic targets. Only some more advanced missiles can undergo small maneuvers,

usually for re-targeting. However, this does not mean that the motion of a foreign target can be determined accurately. In

fact, as vividly expressed in [4], tracking a foreign BT is likely to be “plagued” with a variety of uncertainties, including those

concerning trajectory loft or depression, thrust proﬁle management, target weight, propellant speciﬁc impulse, sensor bias,

and atmospheric parameters. Many of these uncertainties stem from the uncertainty in the target/missile type, the principal

uncertainty in modeling the motion of a foreign BT for the tracking purpose.

Compared with [1], this survey is slightly more tutorial in nature for the beneﬁt of the readers less familiar with the

ballistics or aerodynamics. The same disclaimers as made in the Introduction section of [1] apply to this survey, including

those on the restriction to point targets for temporal behaviors and the interrelationship between dynamics models and tracking

algorithms. The reader should keep in mind that while there have been many extensive studies of BT tracking, not many



Research supported by ONR Grant N00014-00-1-0677 and NSF Grant ECS-9734285.

And possibly a post-boost phase, which involves small maneuvers.

Signal and Data Processing of Small Targets 2001, Oliver E. Drummond, Editor,

559

Downloaded From: https://www.spiedigitallibrary.org/conference-proceedings-of-spie on 24 Nov 2019

results have been published in the open literature. In other words, much of the BT information, particularly target-type

speciﬁc information, such as motion proﬁles (or templates), is classiﬁed and not open to the general public. As a result, this

survey covers only those dynamics models used for BT tracking in the open literature available to us. While some models

covered are applicable to satellite tracking, the emphasis of the survey is on missile tracking.

The rest of the paper is organized as follows. Sec. 2 provides background knowledge in ballistics and aerodynamics that

is necessary to understand the BT motion models presented later. Motion models for the simplest phase, the ballistic ﬂight,

are covered in Sec. 3. This is followed in Sec. 4 by a survey of the models for reentry vehicles. Sec. 5 then describes models

for the boost phase, the most sophisticated phase.

2 Preliminaries

In this section, we provide necessary, rudimentary background information in aerodynamics and ballistics to help the

reader understand the BT motion models presented in the subsequent sections. We hope this will make the text more system-

atic and self-contained.

2.1 Coordinate Systems

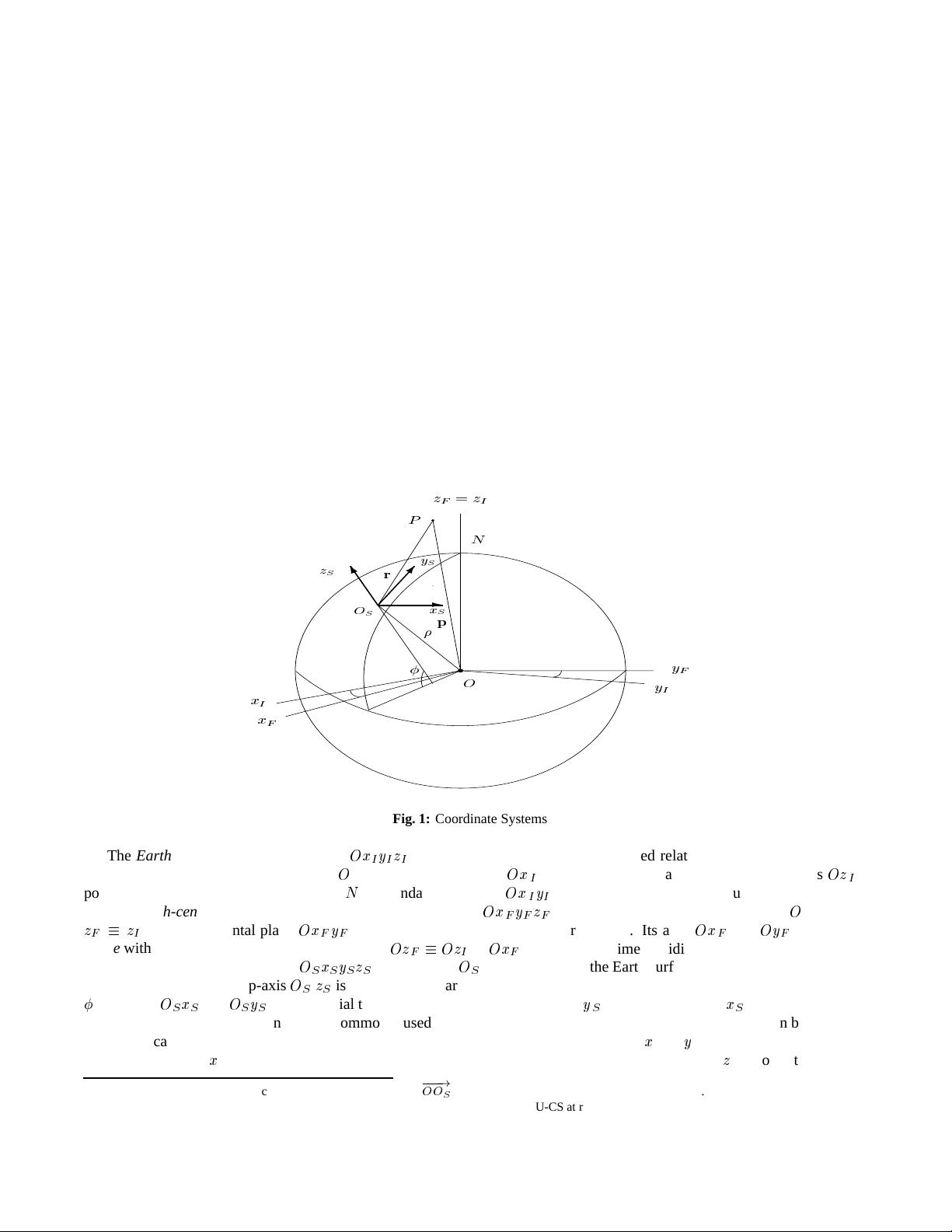
The coordinate systems (CS) commonly used in BT tracking are illustrated in Fig. 1. Much more detailed information on

coordinate systems can be found in e.g. [4, 6, 7, 8, 9, 10].



K



Fig. 1: Coordinate Systems

The Earth-centered inertial (ECI) CS

is ﬁxed in an inertial space (i.e., ﬁxed relative to the “ﬁxed stars”). It

is a right-handed system with the origin

at the Earth center, axis

pointing in the vernal equinox direction, axis

pointing in the direction of the North pole

. Its fundamental plane

coincides with the Earth’s equatorial plane.

The Earth-centered (Earth) ﬁxed (ECF, ECEF, or ECR) CS

also has its origin at the Earth center

, its axis



, and fundamental plane

coincident with the Earth’s equatorial plane. Its axes

and

, however,

rotate with the Earth around the Earth’s spin axis



points to the prime meridian.

The East-North-Up (ENU) CS

has its origin

at some point on the Earth surface or above it (usually at the

location of a sensor). Its Up-axis

is normal to the Earth’s reference ellipsoid,

usually deﬁned by the geodetic latitude



. The axes

and

are tangential to the Earth reference ellipsoid with

pointing North and

East.

Another CS (not depicted in Fig. 1), commonly used in BT tracking, is the radar face (RF) CS

[11, 6]. It can be deﬁned

from the local radar ENU-CS by two angles of rotation [6]. For a phased array radar, the

and

axes of the RF-CS lie on

the radar face, with

axis along the intersection of the radar face with the local horizontal plane, and

is along its normal

Note that the local vertical direction differs from the radial axis

!

. They coincide if a spherical Earth model is used.

Note that it differs from the so-called radar reference CS, which is actually just an ENU-CS at radar site [11].

Proc. SPIE Vol. 4473

560

Downloaded From: https://www.spiedigitallibrary.org/conference-proceedings-of-spie on 24 Nov 2019

(boresight) direction. Such a radar measures the range

and the direction cosines

x=r

and

y=r

This nonorthogonal coordinate system

(

r;u;v

)

is often referred to as the RUV-CS.

In Fig. 1, points

and

(i.e., vectors

!

and



!

) denote target and sensor positions in the ECI-CS or

ECF-CS, respectively. Vector

!

deﬁnes the target position with respect to the sensor in the ENU-CS.

Note that the velocity in the ECF-CS can be expressed in the ECI-CS as follows

= _



;

= _

;

= _

(1)

where

is the Earth rotation rate.

The choice of a CS is a complex issue, depending on numerous factors and related with many elements of a tracking

system [9, 10]. For more information, the reader is referred to [2].

2.2 Total Acceleration

For the tracking purpose, only the most substantial forces that may act on a BT are considered: thrust, aerodynamic forces

(most notably, atmospheric drag and possibly lift), the Earth’s gravity, and, depending on the CS used, possibly the Coriolis

and centrifugal forces. Not all these forces are present at a level that affects signiﬁcantly the motion of a BT in the different

regimes of the trajectory. Speciﬁcally, for most tracking applications the signiﬁcant forces in difference phases are



Boost: Thrust, drag, and gravity.



Coast: Gravity only.



Reentry: Gravity, drag, and lift.

The total acceleration of a BT, in the ECI-CS in a fairly general setting, can be decomposed as

{z }

(2)

where

;

(

;

), and

denote the acceleration components induced by thrust, aerodynamic forces (drag and lift),

and gravity, respectively. Note that the acceleration here is expressed in the ECI-CS (i.e.,

=dt

) in the absolute sense.

If the target motion is considered within a frame ﬁxed to the Earth (e.g., the ENU-CS), then its relative total acceleration

(deﬁned as

for

) should be corrected with the accelerations induced by the Earth’s rotation [3, 4]:





{z }

Coriolis





(



(



))

| {z }

Centrifugal

(3)

where

is the Earth’s angular velocity vector. The terms



and



(



(



))

represent the accelerations due

to the Coriolis

and centrifugal forces, respectively.

Clearly, the entire end-to-end motion of a BT can be modeled by a “wide-band” dynamic model (e.g., nearly constant

velocity, acceleration, jerk, or Singer model [1]) capable of covering the whole range of possible trajectories. Most models

developed for the boost phase, the most sophisticated of all three phases, can serve this purpose. This is, however, rather

crude and not in common use. What is more natural and rational, as well as common practice, is to develop different models

speciﬁc for each trajectory portion that more fully exploit the inherent characteristics of the portion.

We survey next dynamics models for the distinct regimes of a BT proposed/used in the available literature. The motion

phases are ordered with respect to their sophistication levels, rather than to their chronology in the trajectory.

The Coriolis force is an equivalent force induced by the rotation of the Earth that causes the Coriolis effect — the apparent deﬂection of a body in motion