算法设计英文版课件：Chapter 8 The THEORY OF NP_COMPLETENESS.ppt

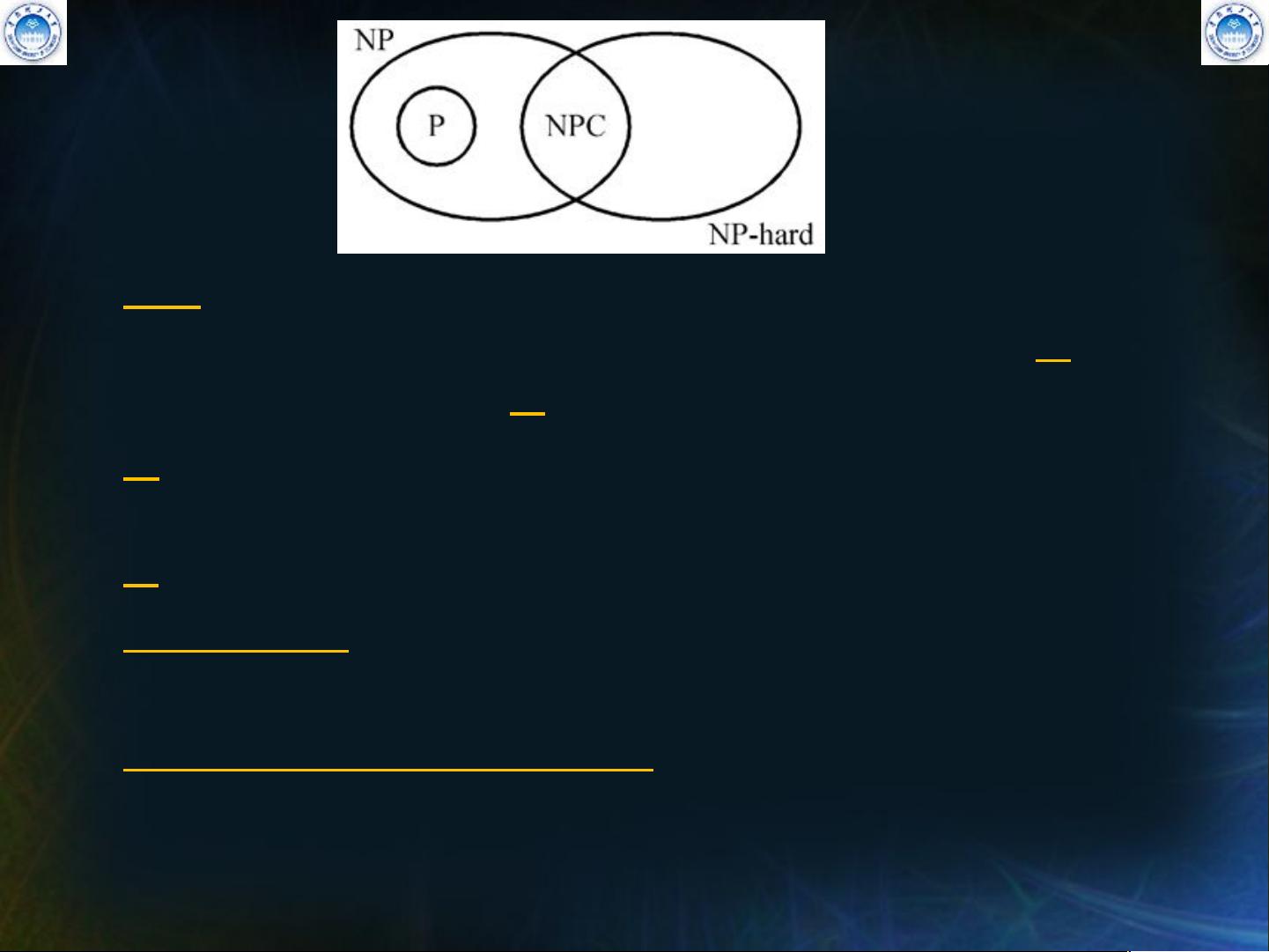
在计算机科学领域，算法设计是核心研究之一，而NP完全性理论是算法设计中的一个关键概念，它涉及到复杂性理论和问题求解的难度评估。本章“Chapter 8 The THEORY OF NP_COMPLETENESS”主要探讨了NP类、P类、NP难问题以及NP完全问题的概念。 NP（非确定性多项式时间）类是决策问题的集合，这些问题可以通过非确定性多项式算法来解决。这意味着存在一种理论上可能的计算模型，即非确定性图灵机，在多项式时间内找到一个正确答案。例如，寻找最短路径的问题或满足特定条件的赋值问题都属于NP问题。 P类则包含了可以通过确定性多项式时间算法解决的问题，即在多项式时间内有确定的步骤和结果来得出解答。P类问题相对而言是较容易处理的，因为它们总能找到一个有效的解决方案。 NP-hard是所有至少与NP中最难的问题一样难的问题集合。即使一个问题不属于NP，如果它可以被任何NP问题归约，那么它就属于NP-hard。NP-hard问题的解决通常意味着解决NP问题的一个有效方法。 接下来，NP完全（NPC）问题是指既是NP-hard又是NP的问题。这些是NP中最难的问题，因为它们不仅是非确定性可解的，而且还是NP类的代表性问题。一个问题是NP完全的，意味着如果找到了它的多项式时间解法，那么所有NP问题都可以在多项式时间内解决。 在课程中提到了问题的归约，这是一种比较问题难度的方法。如果问题A可以通过多项式时间的转换转化为问题B，并且B是已知的NP完全问题，那么我们可以说A是NP-hard的。这个过程对于理解问题的相对复杂性至关重要。 此外，课程还提到了决策问题与优化问题的区别。决策问题只需要“是”或“否”的答案，而优化问题则需要找到最佳解决方案。尽管优化问题更复杂，但通过决策算法可以解决优化问题，通过不断调整参数并使用决策算法来测试，最终找出最优解。 非确定性算法包含两个阶段：猜测和检查。在非确定性阶段，算法会尝试多种可能性，而在检查阶段，算法会验证这些猜测是否正确。如果检查阶段的时间复杂度为多项式，那么算法被认为是NP算法。非确定性操作，如选择和失败，是构建非确定性算法的基础。 非确定性搜索算法和排序问题作为例子被提及。非确定性搜索算法通过猜测可能的解并验证其有效性来工作。排序问题，虽然通常被视为确定性问题，但也可以用非确定性算法来考虑，比如非确定性选择元素进行排序。 NP完全性理论是理解和评估计算难题复杂性的重要工具，对算法设计和复杂性理论的研究具有深远的影响。通过深入学习这一理论，我们可以更好地理解哪些问题在实践中可能是难以解决的，以及如何寻找潜在的近似解法。