
ͼµÄ¶¨ÒåºÍÊõÓï
ͼµÄ¶¨ÒåºÍÊõÓï
ͼµÄ´æ´¢½á¹¹
ͼµÄ´æ´¢½á¹¹
ͼµÄ±éÀúÓëÁ¬Í¨ÐÔ
ͼµÄ±éÀúÓëÁ¬Í¨ÐÔ
×îСÉú³ÉÊ÷
×îСÉú³ÉÊ÷
»î¶¯ÍøÂç
»î¶¯ÍøÂç
×î¶Ì·¾¶
×î¶Ì·¾¶
7.1 ͼµÄ¶¨ÒåºÍÊõÓï
7.1 ͼµÄ¶¨ÒåºÍÊõÓï
ͼÐνṹµÄÐÎʽ¶¨Òå
ͼÐνṹµÄÐÎʽ¶¨Òå
ͼÊÇÓɶ¥µã¼¯ºÏ
ͼÊÇÓɶ¥µã¼¯ºÏ(vertex)
¼°¶¥µã¼äµÄ¹Øϵ¼¯ºÏ×é³Éµ
¼°¶¥µã¼äµÄ¹Øϵ¼¯ºÏ×é³Éµ
ÄÒ»ÖÖÊý¾Ý½á¹¹
ÄÒ»ÖÖÊý¾Ý½á¹¹£º
Graph£½(
Graph£½(
V
V
,
,
R
R
)
)
ÆäÖУº
ÆäÖУº
V
V
= {
= {
x
x
|
|
x
x
Î
Î
ij¸öÊý¾Ý¶ÔÏó}
ij¸öÊý¾Ý¶ÔÏó}
£¬
£¬
ÊǶ¥µãµÄÓÐÇî·Ç¿Õ¼¯ºÏ£»
ÊǶ¥µãµÄÓÐÇî·Ç¿Õ¼¯ºÏ£»
R——±ßµÄÓÐÏÞ¼¯ºÏ
R——±ßµÄÓÐÏÞ¼¯ºÏ
R
R
= {(
= {(
x
x
,
,
y
y
) |
) |
x
x
,
,
y
y
Î
Î
V
V
} ÎÞÏòͼ
} ÎÞÏòͼ
»ò
»ò
R
R
= {<
= {<
x
x
,
,
y>
y>
|
|
x
x
,
,
y
y
Î
Î
V
V
&&
&&
Path
Path
(
(
x
x
,
,
y
y
)}ÓÐÏòͼ
)}ÓÐÏòͼ
ÊǶ¥µãÖ®¼ä¹ØϵµÄÓÐÇºÏ£¬Ò²½Ð×ö±ß(edge)¼¯º
ÊǶ¥µãÖ®¼ä¹ØϵµÄÓÐÇºÏ£¬Ò²½Ð×ö±ß(edge)¼¯º
Ï¡£
Ï¡£
Path
Path
(
(
x
x
,
,
y
y
)
)
±íʾ´Ó
±íʾ´Ó
x
x
µ½
µ½
y
y
µÄÒ»Ìõµ¥Ïòͨ·,
µÄÒ»Ìõµ¥Ïòͨ·,
ËüÊÇÓз½ÏòµÄ¡£x»¡Î²£¬y»¡Í·
ËüÊÇÓз½ÏòµÄ¡£x»¡Î²£¬y»¡Í·

ÓÐÏòͼÓëÎÞÏòͼ
ÓÐÏòͼÓëÎÞÏòͼ
ÓÐÏòͼÖУº±ßÓÃ<x, y>±íʾ£¬ÇÒxÓëyÊÇÓÐÐòµÄ¡£
ÓÐÏòͼÖУº±ßÓÃ<x, y>±íʾ£¬ÇÒxÓëyÊÇÓÐÐòµÄ¡£
a. ÓÐÏòͼÖеı߳ÆΪ“»¡”
a. ÓÐÏòͼÖеı߳ÆΪ“»¡”
b. x——»¡Î²»ò³õʼµã y——»¡Í·»òÖն˵ã
b. x——»¡Î²»ò³õʼµã y——»¡Í·»òÖն˵ã
ÎÞÏòͼ£º±ßÓÃ(x, y) ±íʾ£¬ÇÒ¶¥xÓë yÊÇÎÞÐòµÄ¡£
ÎÞÏòͼ£º±ßÓÃ(x, y) ±íʾ£¬ÇÒ¶¥xÓë yÊÇÎÞÐòµÄ¡£
Íêȫͼ
Íêȫͼ
ÔÚ¾ßÓÐ
ÔÚ¾ßÓÐ
n
n
¸ö¶¥µãµÄÓÐÏòͼÖУ¬×î´ó»¡ÊýΪ
¸ö¶¥µãµÄÓÐÏòͼÖУ¬×î´ó»¡ÊýΪ
n
n
(
(
n
n
-1)
-1)
ÔÚ¾ßÓÐ
ÔÚ¾ßÓÐ
n
n
¸ö¶¥µãµÄÎÞÏòͼÖУ¬×î´ó±ßÊýΪ
¸ö¶¥µãµÄÎÞÏòͼÖУ¬×î´ó±ßÊýΪ
n
n
(
(
n
n
-1)/2
-1)/2
¶¥µãµÄ¶È
¶¥µãµÄ¶È
ÎÞÏòͼ£ºÓë¸Ã¶¥µãÏà¹ØµÄ±ßµÄÊýÄ¿
ÎÞÏòͼ£ºÓë¸Ã¶¥µãÏà¹ØµÄ±ßµÄÊýÄ¿
ÓÐÏòͼ
ÓÐÏòͼ
£º
£º
Èë¶È
Èë¶È
ID(
ID(
v
v
)
)
£ºÒԸö¥µãΪͷµÄ»¡µÄÊýÄ¿
£ºÒԸö¥µãΪͷµÄ»¡µÄÊýÄ¿
³ö¶È
³ö¶È
OD(
OD(
v
v
)
)
£ºÒԸö¥µãΪβͷµÄ»¡µÄÊýÄ¿
£ºÒԸö¥µãΪβͷµÄ»¡µÄÊýÄ¿

ÔÚÓÐÏòͼÖÐ,
ÔÚÓÐÏòͼÖÐ,
¶¥µãµÄ¶ÈµÈÓڸö¥µãµÄÈë¶ÈÓë³ö¶ÈÖ®ºÍ¡£
¶¥µãµÄ¶ÈµÈÓڸö¥µãµÄÈë¶ÈÓë³ö¶ÈÖ®ºÍ¡£
ÁÚ½Óµã
ÁÚ½Óµã
ÎÞÏòͼ£ºÁ½¶¥µãÖ®¼äÓÐÌõ±ß£¬ÔòÁ½¶¥µã»¥ÎªÁÚ½
ÎÞÏòͼ£ºÁ½¶¥µãÖ®¼äÓÐÌõ±ß£¬ÔòÁ½¶¥µã»¥ÎªÁÚ½


x —— y ( x ,y )
x —— y ( x ,y )
ÓÐÏòͼ
ÓÐÏòͼ
£º
£º
´Óxµ½yÓÐÒ»Ìõ»¡£¬ÔòyÊÇxµÄÁڽӵ㣬
´Óxµ½yÓÐÒ»Ìõ»¡£¬ÔòyÊÇxµÄÁڽӵ㣬
µ«x²»ÊÇyµÄÁÚ½Óµã
µ«x²»ÊÇyµÄÁÚ½Óµã
x y <
x ,y
x ,y >
Ȩ
Ȩ
ijЩͼµÄ±ß¾ßÓÐÓëËüÏà¹ØµÄÊý,
ijЩͼµÄ±ß¾ßÓÐÓëËüÏà¹ØµÄÊý,
³Æ֮ΪȨ¡£ÕâÖÖ´øȨͼ½Ð×öÍøÂç¡£
³Æ֮ΪȨ¡£ÕâÖÖ´øȨͼ½Ð×öÍøÂç¡£
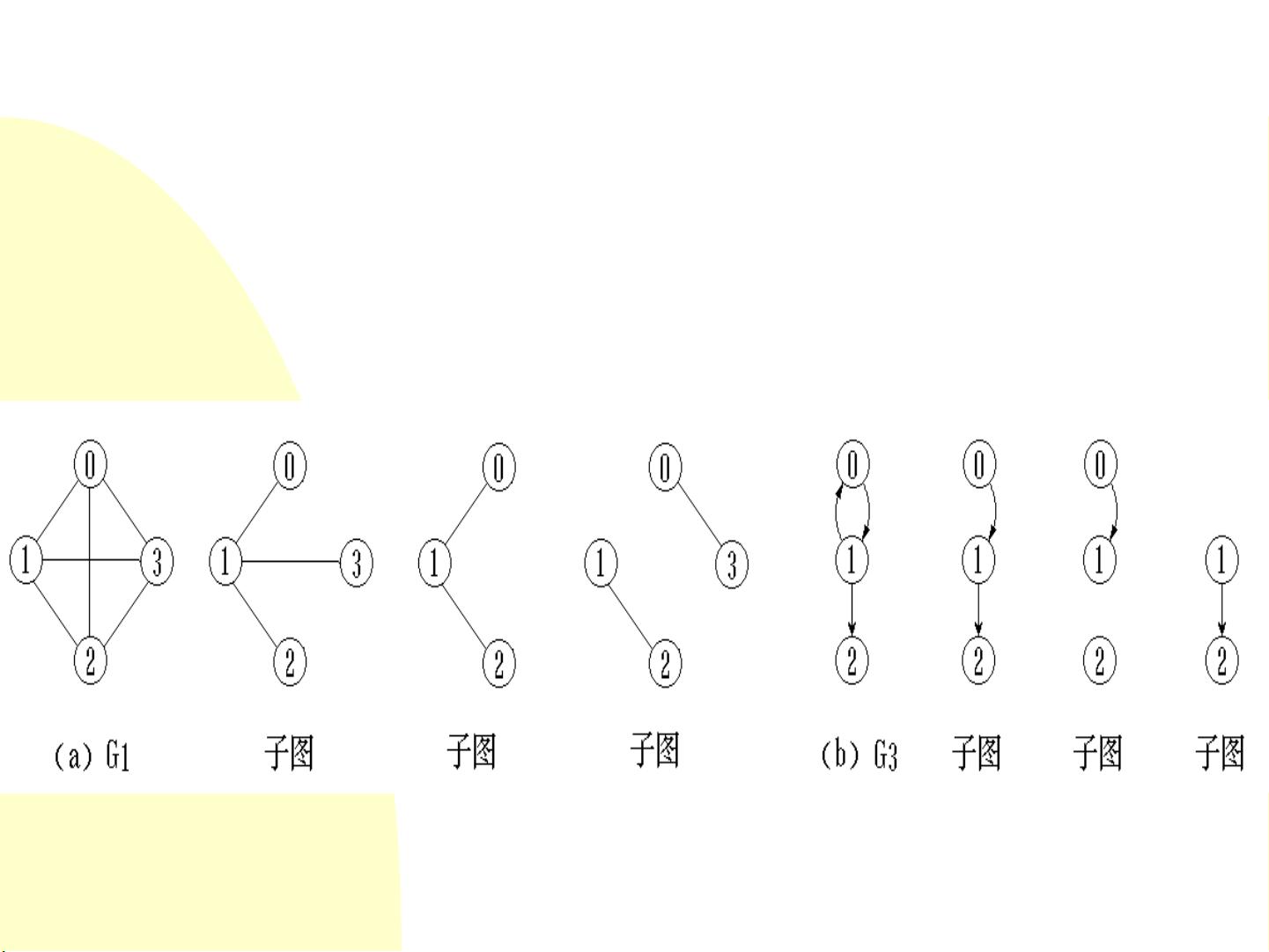
×Óͼ
×Óͼ
ÉèÓÐÁ½¸öͼ G£½(
ÉèÓÐÁ½¸öͼ G£½(
V
V
,
,
E
E
) ºÍ G‘£½(
) ºÍ G‘£½(
V
V
’,
’,
E
E
‘)
‘)
¡£Èô
¡£Èô
V
V
’
’
Í
Í
V
V
ÇÒ
ÇÒ
E
E
‘
‘
Í
Í
E
E
, Ôò³Æ ͼG’ ÊÇ Í¼G
, Ôò³Æ ͼG’ ÊÇ Í¼G
µÄ×Óͼ¡£
µÄ×Óͼ¡£
















