《有理数的乘方 (2).ppt》的讲解涵盖了有理数乘方的基本概念、性质及其应用。乘方是数学中的一个重要运算,它表示的是相同数字相乘的简便表示方式。例如,2的3次方(2^3)表示的就是2乘以自己3次,即2×2×2=8。
1. **乘方的意义和读写**:
- 在乘方中,`a^n`表示`a`自乘`n`次,其中`a`称为底数,`n`称为指数。例如,2的4次方(2^4)读作“2的4次方”,写作2×2×2×2。
2. **幂的性质**:
- 正数的任何次幂都是正数,如:(3)^5 = 3×3×3×3×3。
- 负数的奇次幂是负数,如:(-2)^3 = (-2)×(-2)×(-2) = -8。
- 负数的偶次幂是正数,如:(-2)^2 = (-2)×(-2) = 4。
- 幂的乘法法则:`a^m * a^n = a^(m+n)`。
- 幂的除法法则:`a^m / a^n = a^(m-n)`。
- 幂的幂法则:`(a^m)^n = a^(m*n)`。
3. **运算实例**:
- 例题中,如(-2)×(-2)×(-2)= (-2)^3 = -8,展示了负数奇次幂为负的性质。
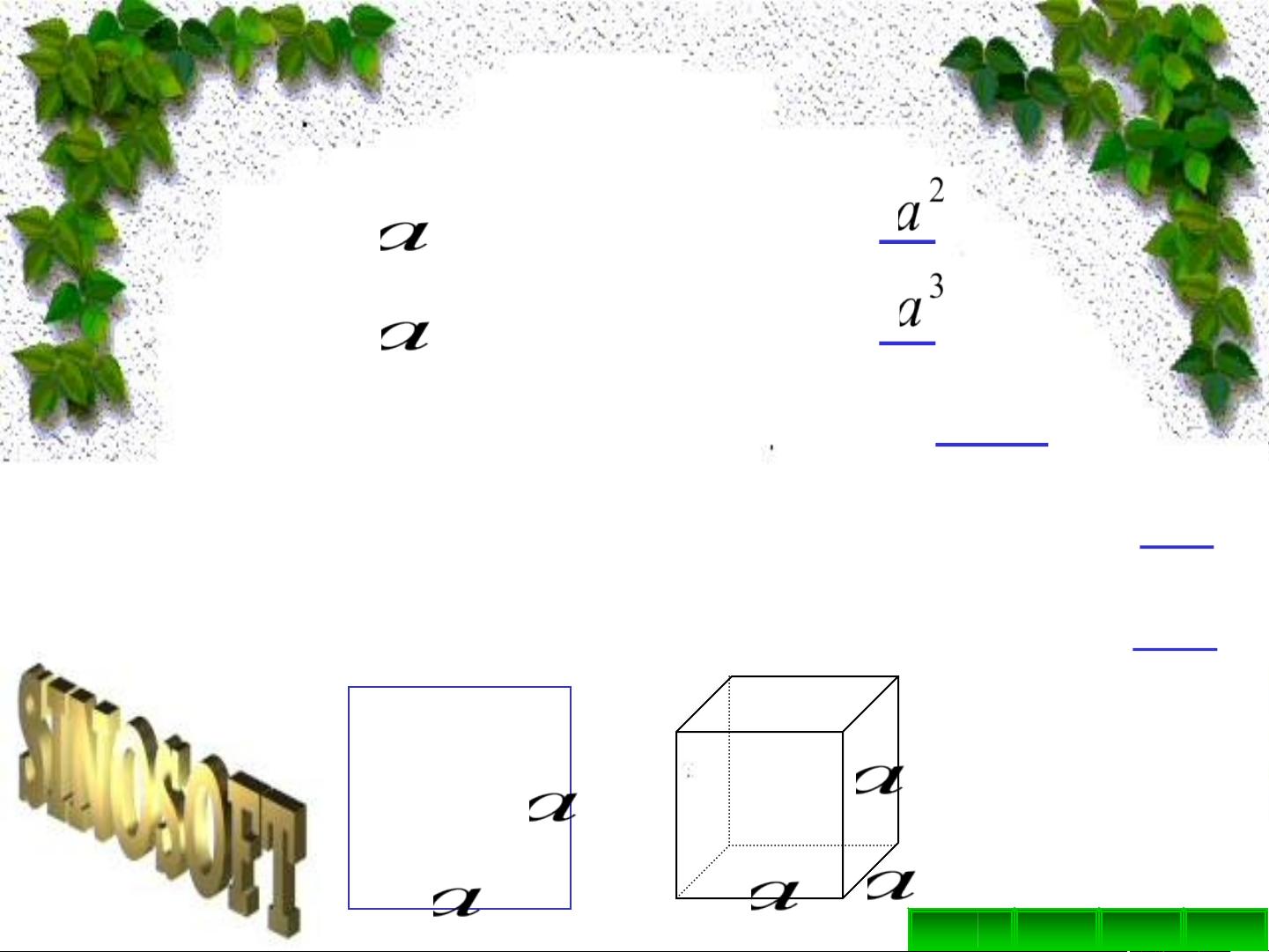
- 练习一的题目涵盖了正方形面积和正方体体积的计算,以及负数乘方的运算,如(-1)×(-2)×(-3)×(-4)×5,运用了负数乘法和乘方的规则。
4. **能力培养**:
- 通过这些运算,可以提升学生的运算能力,同时培养他们观察、类比、归纳和知识迁移的能力。
5. **实际应用**:
- 文件中的纸张对折问题,展示了乘方在实际问题中的应用。例如,对折10次,纸张的张数可以用2^10表示,强调了乘方在解决复杂重复计算问题时的便捷性。
6. **练习题目**:
- 练习二要求将乘法表达式转换为乘方形式,如1×1×1×1×1×1×1可以写成1^7。
- 练习三则涉及判断幂的正负,比如(-1)^2是正数,(-1)^3是负数,这进一步巩固了幂的性质。
- 练习四包含具体的乘方计算,如11的平方、-2的立方等。
总结来说,本讲义旨在帮助学生理解和掌握有理数的乘方,包括其意义、读写、性质以及计算方法,同时通过练习题强化理解和应用。这些基础知识对于后续的代数学习至关重要。