有理数的乘方 (5).ppt

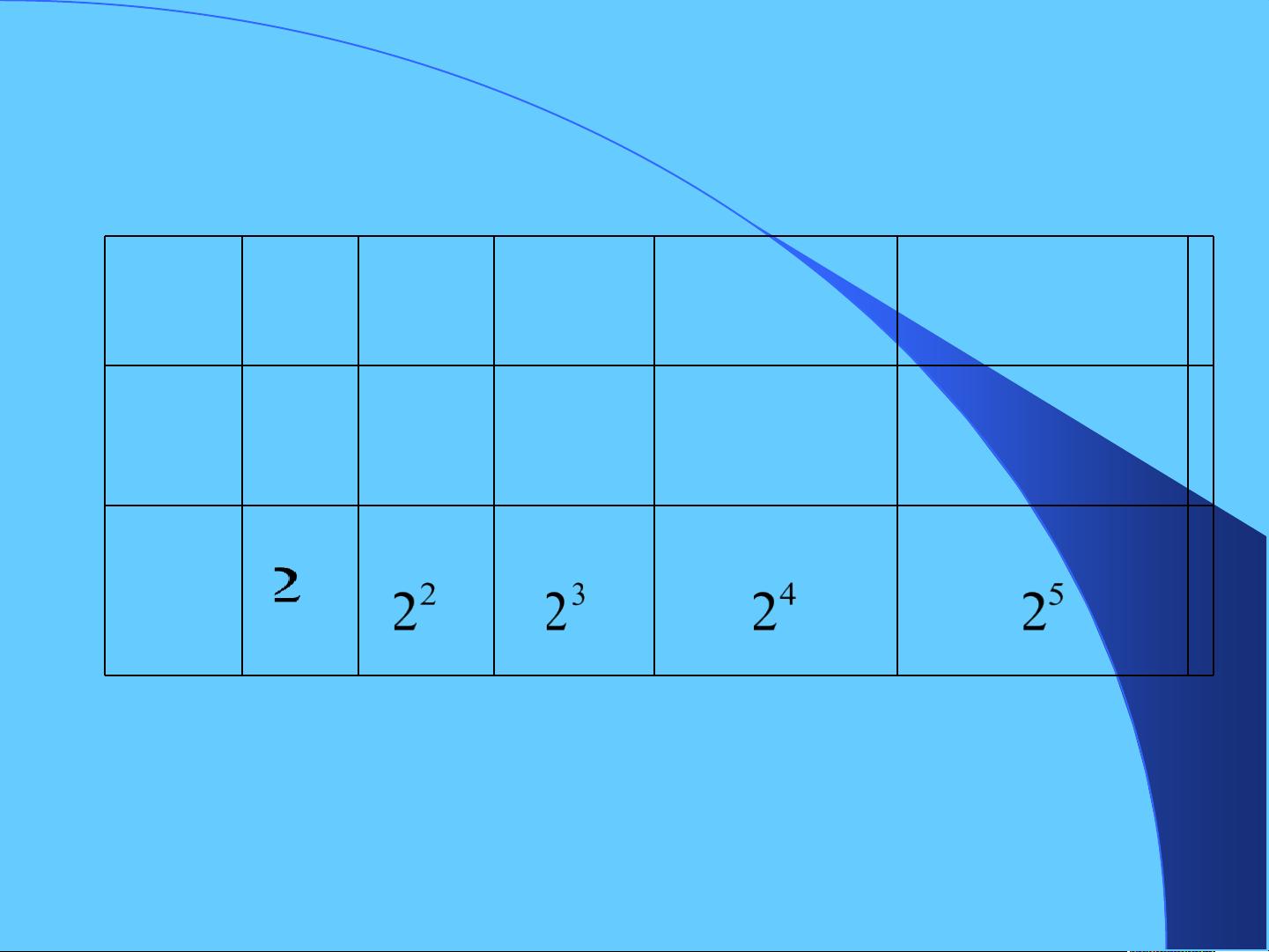
有理数的乘方是数学中的基本概念，尤其在初等代数中占有重要地位。在七年级上学期的数学课程中，学生会接触到这一主题。乘方是指数学上的一种运算，它表示将一个数自乘若干次。在这个过程中，自乘的次数被称为指数，而被乘的数称为底数。例如，在表达式 \(2^4\) 中，2是底数，4是指数，结果是16，因为 \(2 \times 2 \times 2 \times 2 = 16\)。 乘方的规则简单明了： 1. 正数的任何次幂都是正数，如 \(3^5 = 243\)。 2. 负数的奇数次幂是负数，如 \((-2)^3 = -8\)。 3. 负数的偶数次幂是正数，如 \((-2)^2 = 4\)。 4. 0的任何正整数次幂都是0，因为任何数与0相乘结果都是0，如 \(0^5 = 0\)。 在实际应用中，乘方可以帮助我们解决许多问题。例如，当我们需要计算一个数连续相乘时，使用乘方可以简化计算。在给定的例子中，纸张的层数可以通过将2乘以自己n次来计算，即 \(2^n\)，这就是乘方的概念。如果对折一次，纸张的层数就是2，两次就是4，以此类推。 另一个例子是细胞分裂问题，如果一个细胞每30分钟分裂成两个，那么3小时后的细胞数量就是 \(2^{6}=64\) 个，因为3小时相当于6个30分钟周期。同样，n小时后的细胞数量可以用 \(2^{2n}\) 来表示，这里的2是每次分裂增加的数量（即2倍），n是分裂的次数。 在纸张折叠的问题中，尽管0.1毫米的纸张折叠40次后高度会变得非常巨大，但它仍然无法达到从地球到月球的距离，因为即使折叠次数再多，纸张的初始厚度限制了它的总体积。然而，这个问题提醒我们，指数增长的力量是惊人的，即使是很小的初始值，通过连续的乘方运算，也可以得到非常大的结果。 在生活中，乘方运算的应用无处不在。比如，银行的复利计算就涉及到乘方，如果你有一笔存款，年利率是5%，一年后你得到的利息不仅是本金的5%，而是包括了之前利息的5%。再如，人口增长模型，经济增长率，病毒传播速度等等，都依赖于乘方运算来预测未来的趋势。 作业部分要求学生完成P58的练习题，并在生活中找到一个运用乘方运算的例子。这不仅有助于巩固课堂所学，还能引导学生发现数学在日常生活中的实际应用。例如，可以考虑一个家庭每月存款一定的金额，若干年后存款总额的增长就可以用乘方来描述。通过这样的实践活动，学生能够更好地理解和运用有理数的乘方。