正态分布,又称为高斯分布,是一种在统计学中极其重要的连续概率分布。它在自然界、社会科学以及工程技术等领域有着广泛的应用,特别是在描述许多随机变量的分布情况时,如人的身高、体重、智商等。正态分布的特点是其概率密度函数呈钟形曲线,中心对称,且具有以下特性:
1. **对称性**:正态分布的曲线是对称的,即分布的左右两侧形状完全相同。中心点是分布的均值(μ),也是曲线的最高点。
2. **集中性**:大部分观测值集中在均值附近,随着与均值的距离增加,观测值出现的频率逐渐降低,呈现出一种“中间多,两头少”的分布形态。
3. **扩散性**:分布的宽度由标准差(σ)决定,σ越大,分布越分散,数据点更可能出现在远离均值的地方;σ越小,分布越集中,数据点更可能接近均值。
4. **标准化转换**:对于任意一个服从正态分布的随机变量X,可以通过标准化转换(Z变换)将其转化为标准正态分布,即U = (X - μ) / σ。标准正态分布的均值为0,标准差为1,它在统计分析中起到重要的桥梁作用,因为它允许我们将不同分布的数据进行比较和转换。
5. **面积规则**:正态分布曲线下的总面积为1,代表100%的可能性。对于任何正态分布,其均值左侧和右侧各占一半面积,即均值下方的面积为0.5,而标准差决定了特定区间内的数据比例。例如,68%的数据位于均值±1个标准差内,95%的数据位于均值±2个标准差内,而99.7%的数据位于均值±3个标准差内,这个规则被称为68-95-99.7法则。
6. **概率密度函数**:正态分布的概率密度函数公式为f(x) = (1/σ√(2π)) * e^(-((x-μ)^2)/(2σ^2)),其中e是自然对数的底数,π是圆周率。
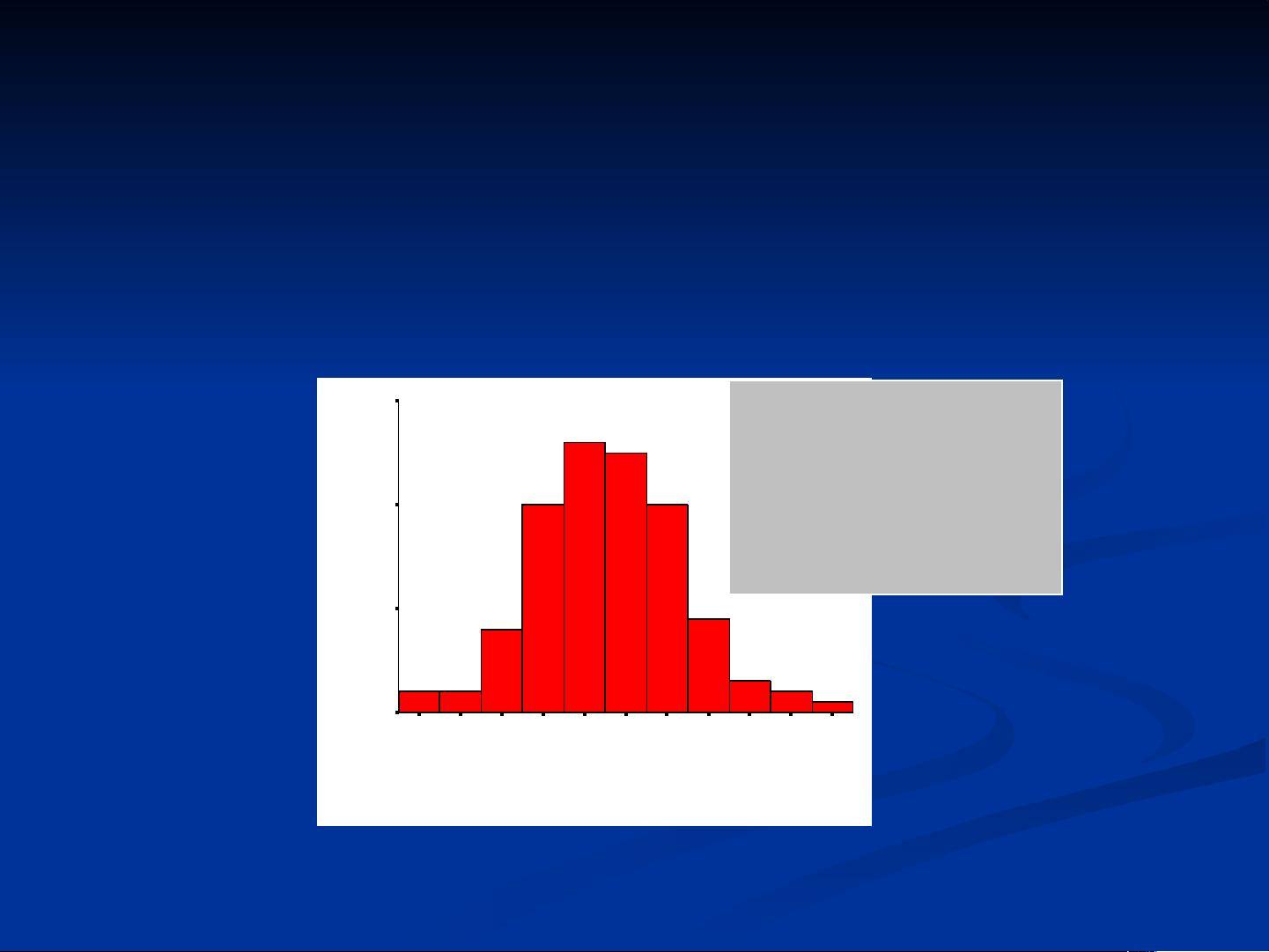
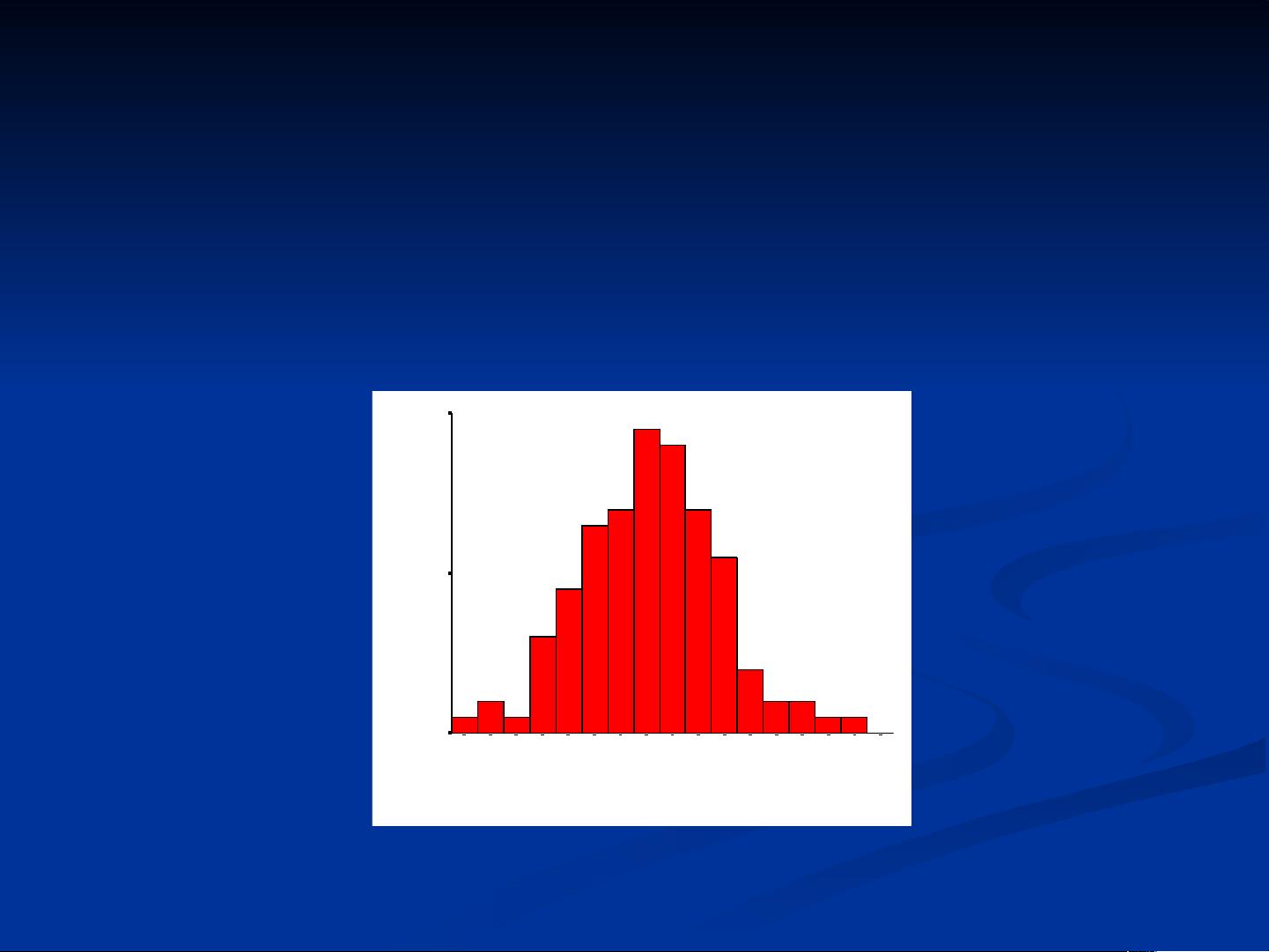
在实际应用中,正态分布是进行假设检验、置信区间的计算以及预测分析的基础。例如,在上述例子中,通过绘制13岁女孩身高的频数分布图,可以看出数据大致符合正态分布,这有助于我们理解数据的集中趋势和变异程度,并可以进一步进行统计推断。
正态分布是一种描述数值型数据分布的经典模型,它的理论和应用贯穿于整个统计学,对于理解和处理各种数据问题至关重要。掌握正态分布的特性,不仅可以帮助我们更好地理解数据,还能有效进行数据分析和决策。