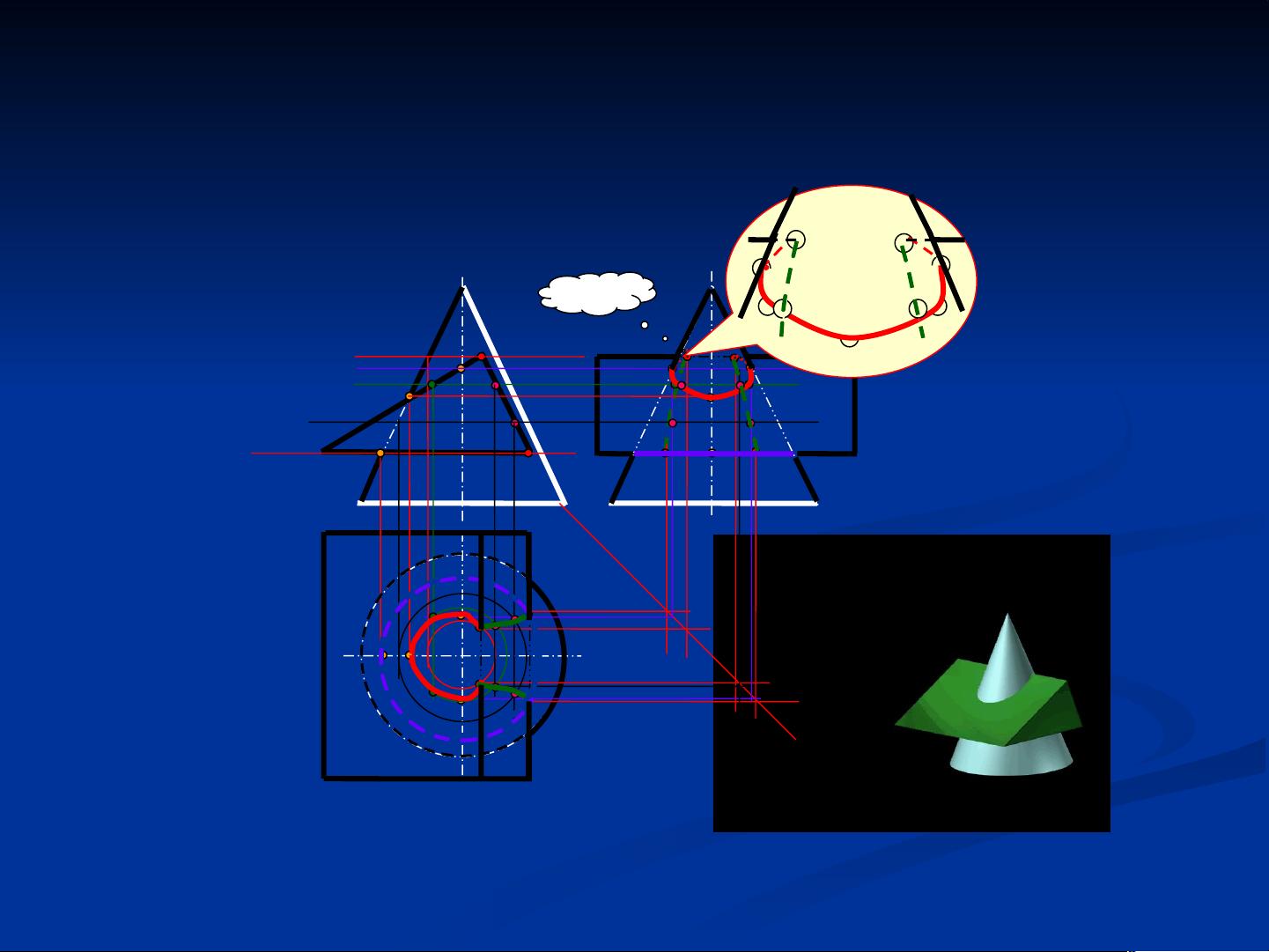
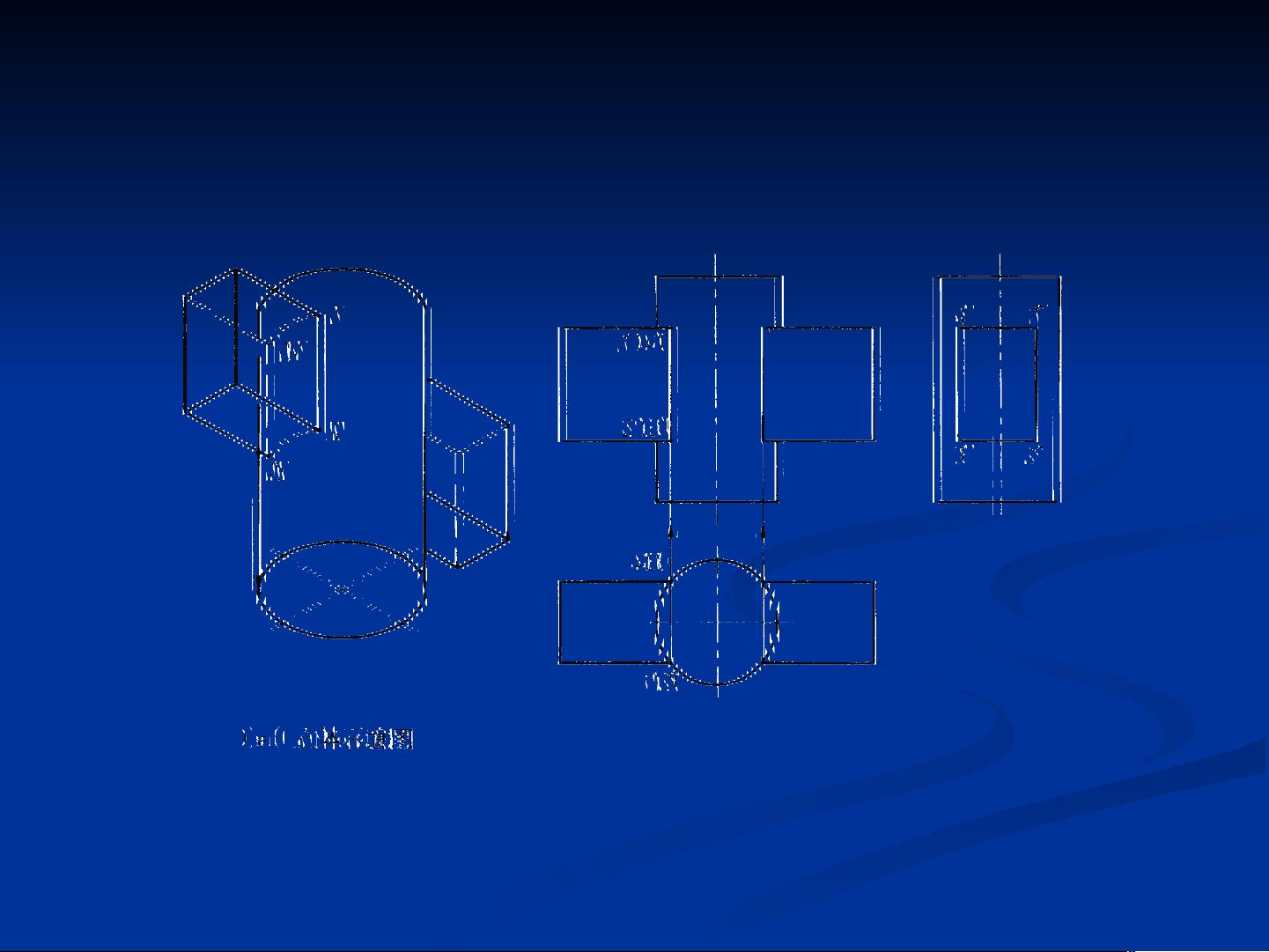
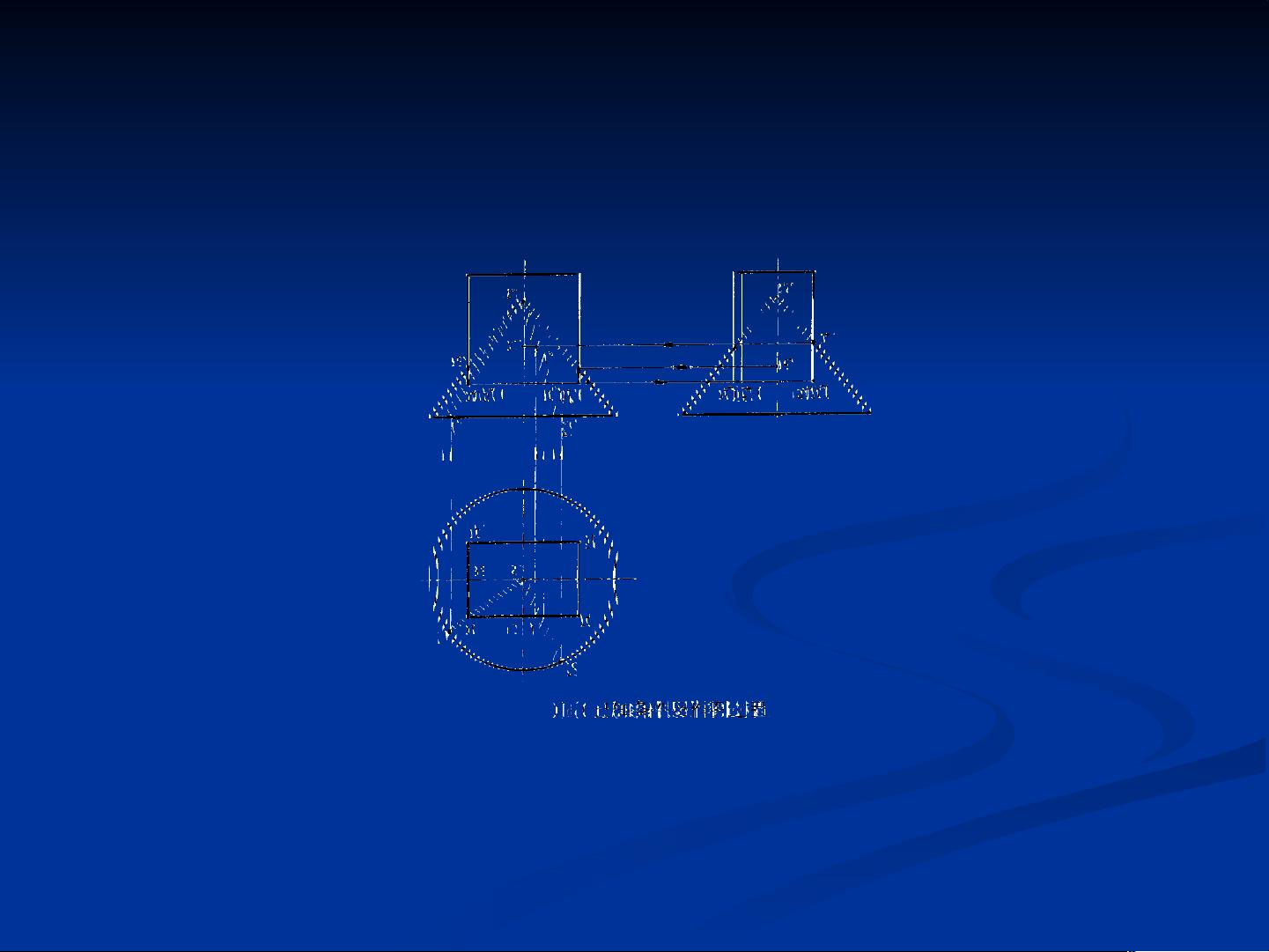
woshifafuge
- 粉丝: 8
- 资源: 58万+
最新资源
- 机械设计物流双托盘提升机sw18可编辑全套设计资料100%好用.zip
- 基于Java的学院教学工作量统计系统源码(java毕业设计完整源码).zip
- 三菱plc搭配四轴雅马哈机械手在线检测收料案例程序 (包涵CAD电气图纸,plc程序,人机界面,机器人程序,BOM表)程序中应用到CClink通讯,232串口通讯,数据采集伺服定位控制
- LibUsbDotNet C#
- 机械设计消毒袋封口机x_t全套设计资料100%好用.zip
- 证件照处理的代码演示以及说明
- 基于java的招聘求职系统源码(java毕业设计完整源码).zip
- 基于Java的校园二手商品交易系统设计与实现源码(java毕业设计完整源码).zip
- 基于JAVA的校园二手物品交易系统的设计与实现源码(java毕业设计完整源码+LW).zip
- 学生考试表现影响因素数据集.zip
- 基于Java的校园消费点评系统源码(java毕业设计完整源码).zip
- 图像加解密的代码展示以及说明
- 基于Java的校园自助洗衣服务管理系统的设计与实现源码(java毕业设计完整源码).zip
- 基于Python的图像加解密技术实现
- 线性自抗扰(LADRC)的stm32f1程序,实现用编码器反馈控制直流电机调速,控制器采用加了TD的LADRC,控制效果良好,.h和.c分开,代码清晰有注释 有调试说明
- 【Endnote 文献输出样式Style Chinese std GBT7714 下载和使用】
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈