管理运筹学对策论PPT学习教案.pptx

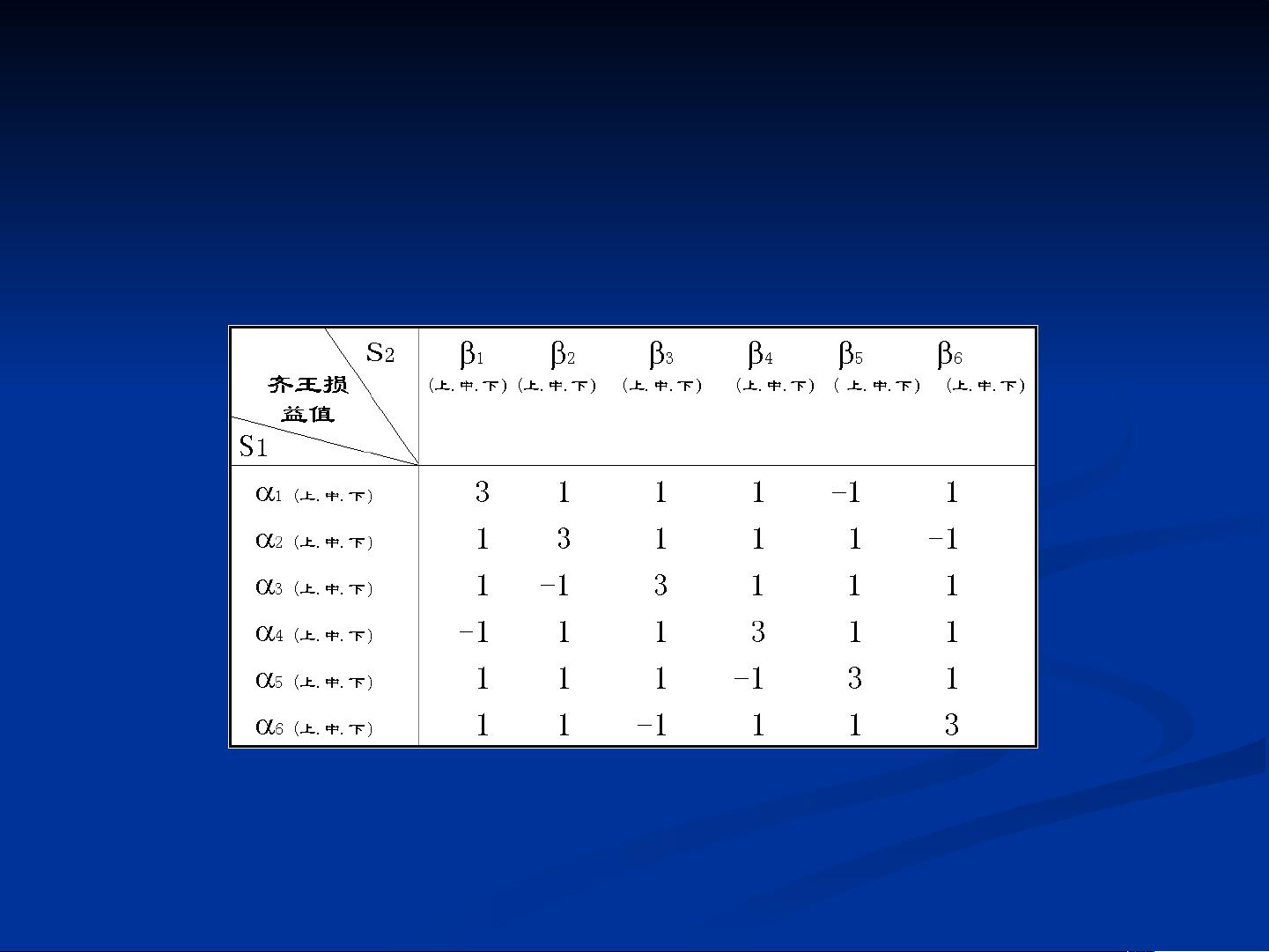
【管理运筹学对策论】是运筹学的一个分支，主要研究在不确定环境中，多个决策者（局中人）如何制定策略以最大化自己的利益。它广泛应用于管理、经济、军事等领域的决策问题。 1. **对策论的基本概念** - **局中人**：对策论中的参与者，每个局中人都有自己的目标和策略。 - **策略集**：局中人可选择的一系列行动方案，构成其策略空间。 - **局势与益损值**：当每个局中人选择一个策略时，形成一个局势。局势决定所有局中人的收益，益损值是量化这一结果的指标。 2. **二人有限零和对策** - **局中人数**：只有两个局中人参与。 - **策略有限**：每个局中人的策略集合是有限的。 - **零和性质**：对于每个局势，两个局中人的益损值之和为零，即一方的收益等于另一方的损失。 3. **矩阵对策** - **矩阵表示**：通过矩阵来表示局中人的策略和相应的益损值，称为赢得矩阵。 - **记号**：G = {S1, S2, A}，其中S1和S2分别代表局中人的策略集，A为赢得矩阵。 4. **最优纯策略** - **最优策略**：在甲的赢得矩阵中，每个策略对应着乙的不同策略的益损值。最优纯策略是指无论对方采取何种策略，己方都能获得最大或最小的益损值。 - **鞍点**：如果存在一个策略对（α2，β3），使得甲采取α2时无论如何乙选择策略，甲至少可以获得一定益损值，而乙采取β3时无论如何甲选择，乙至少可以获得一定益损值，这个策略对就是对策的鞍点，对应的益损值为对策的值V。 5. **混合策略** - **不存在最优纯策略**：如果最大最小值不相等，即max min aij ≠ min max aij，意味着不存在最优纯策略，需要寻找混合策略。 - **混合策略求解**：在这种情况下，局中人可以以一定的概率选择不同的策略，以期望获得最佳平均收益。 例如，一个简单的矩阵对策可能涉及到两家公司甲和乙的选择。甲有三个策略，乙有四个策略，可以通过建立赢得矩阵来分析每种组合下的益损。通过计算最大最小值和最小最大值，可以找出甲和乙的最优纯策略，若两者不等，则需要寻找混合策略。混合策略涉及到为每个纯策略分配一个概率，以最大化期望益损值。 对策论的理论和方法可以帮助决策者在不确定环境下制定出更合理的策略，以应对竞争对手的行为，达到最优化的决策效果。在实际应用中，如赛马博弈、市场竞争分析、资源分配等问题，都可以运用对策论的理论进行分析和决策。