工程中的计算方法课件8 启发式算法.pdf

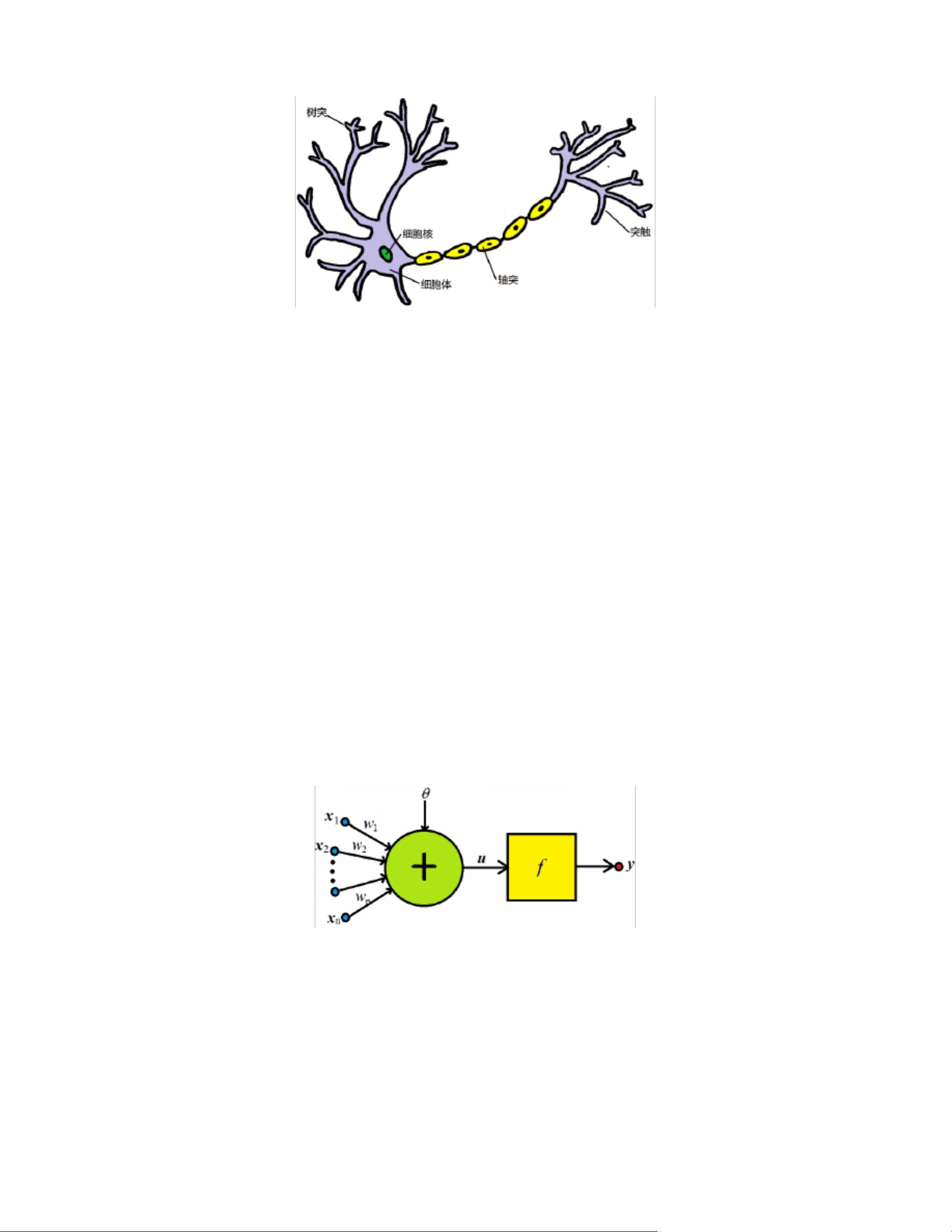
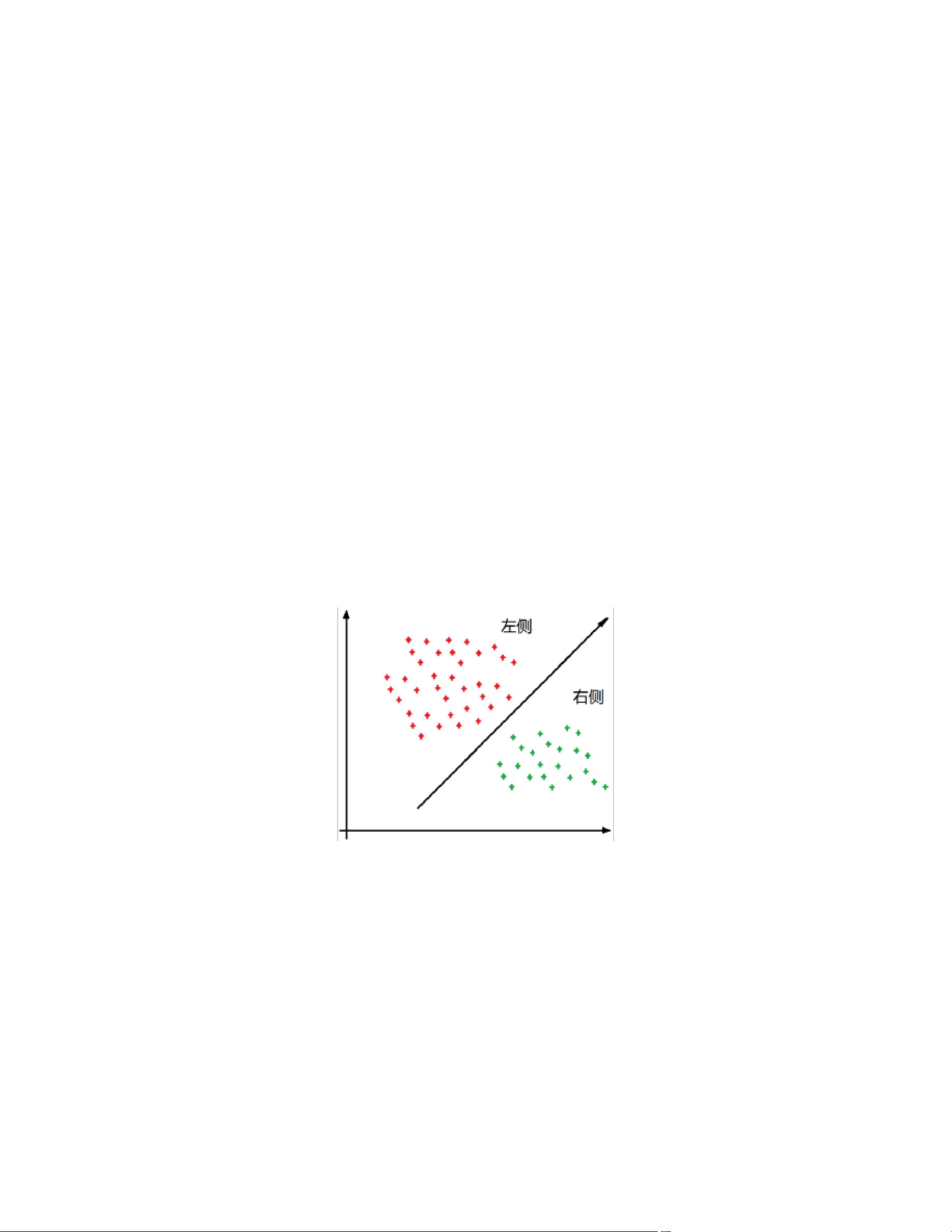
《工程中的计算方法》课件第八章主要探讨了启发式算法，这是一种能够在复杂问题中寻找全局最优解的通用算法。启发式算法源于对自然界规律的模仿，比如生物进化和神经元模型，因此它们具有较强的全局优化能力和并行处理潜力。 启发式算法可以分为两大类：直接搜索法和迭代法。直接搜索法适用于小规模的解空间，而迭代法则依赖于初始解，通常用于局部优化。然而，对于高维度的解空间，这两种方法往往效率低下，难以找到全局最优解。为了解决这一问题，人们发展出了进化算法，如模拟退火算法、遗传算法、粒子群优化算法和人工神经网络算法。 模拟退火算法（Simulated Annealing, SA）灵感来源于金属冷却过程，通过接受次优解来避免早熟收敛，从而在搜索空间中实现全局探索。遗传算法（Genetic Algorithm, GA）模拟生物进化过程，通过选择、交叉和变异操作来逐步优化种群，寻找最优解。粒子群优化算法（Particle Swarm Optimization, PSO）受到鸟群飞行行为的启发，通过粒子间的交互和个体的最优位置更新来寻找全局最优。人工神经网络算法（Artificial Neural Network, ANN）则是模仿生物神经元网络，通过大量数据的训练和权重调整，实现复杂问题的学习和处理。 神经元模型在启发式算法中占有重要地位。生物神经元由树突、始段和轴突组成，负责接收、处理和传递信息。1943年，心理学家W. McCulloch和数学家W. Pitts提出的M-P模型，将神经元简化为数学模型，其核心是线性累加的输入和二进制输出。神经元模型通过激活函数将输入转换为非线性输出，这种模型可以被视为简单的分类器，通过调整权重和偏置，能够划分输入空间，实现分类任务。 遗传算法由J. Holland在1975年提出，它通过模拟自然选择和遗传过程来优化解决方案。这个算法包括选择、交叉和变异操作，能够适应各种优化问题，广泛应用于自动控制、生产调度、图像处理、机器学习、数据挖掘、CAD/CAM和产品设计等领域。 启发式算法借鉴了自然界中的智慧，提供了解决复杂优化问题的有效途径。无论是模拟生物进化过程的遗传算法，还是基于神经元模型的神经网络，都是为了在庞大的解空间中高效地寻找最优解。这些算法的理论基础和实际应用展示了人类对自然规律的深刻理解和巧妙运用。