一级倒立摆双路 PD 控制
今天来说一下,一级倒立摆的控制问题。这个限制一下,倒立摆的参数和上一篇文章的
一样。这里就再啰嗦一下:小车质量
1M kg=
,单摆的质量
0.1m kg=
,单摆质心到支点的
长度
0.5l m=
,重力加速度
2
9.8 /g m s=
,
F
为加在小车上的力,
2
1
(2 )
3
J m l=
为杆的转
动惯量。
[ 2.4,2.4]x Î -
表示小车中心相对于轨道中点的位置,右侧为正;
q
表示单摆相对
于倒立位置的倾角,角度为顺时针为正。注意:这里的位置和角度的正方向,是模型本身的。
如果只引用一路 PID 对角度进行控制的时候,我们会发现,参数调节,角度是可以控制
好的,但是位置项却控制不好的。这是为什么呢,因为输出里之和角度有关,没有位置的信
息。就好像一个演员,在顶杆的时候,如果只盯着杆看,不注意脚下,是很容易走出舞台的,
那时就没工资了。这里角度信息不包含位置信息的意思,假设解读为θ,角速度为Ω,此时
坐标可以为任何值,而不是一个确定的值。这个角度来说倒立摆是欠驱动系统。
后来查文献,就看到双路 PD 控制了。对于这个为什么可以,在实验后再看看原因。
当使用 PID 控制的时候,我们需要建立一个测量系统。这也是为什么强调上面的正方向
是模型本身的。于是,假设力向右为正的话:假设角度为 5°的话,此时,从物理角度来说,
我们需要施加一个向右的力,才能使倒立摆的角度变成参考值 0°,而根据负反馈来看,误
差=参考值-观测值。那么这个观测值就需要是负值,才能使得误差为正值,乘以相应的系数
得到的力才能为正。因此,对于测量角度的正方向为逆时针。同理,可以得到对位置想的观
测正方向为向右为正。但是,经过试验发现,对于位置的观测得向左为正。
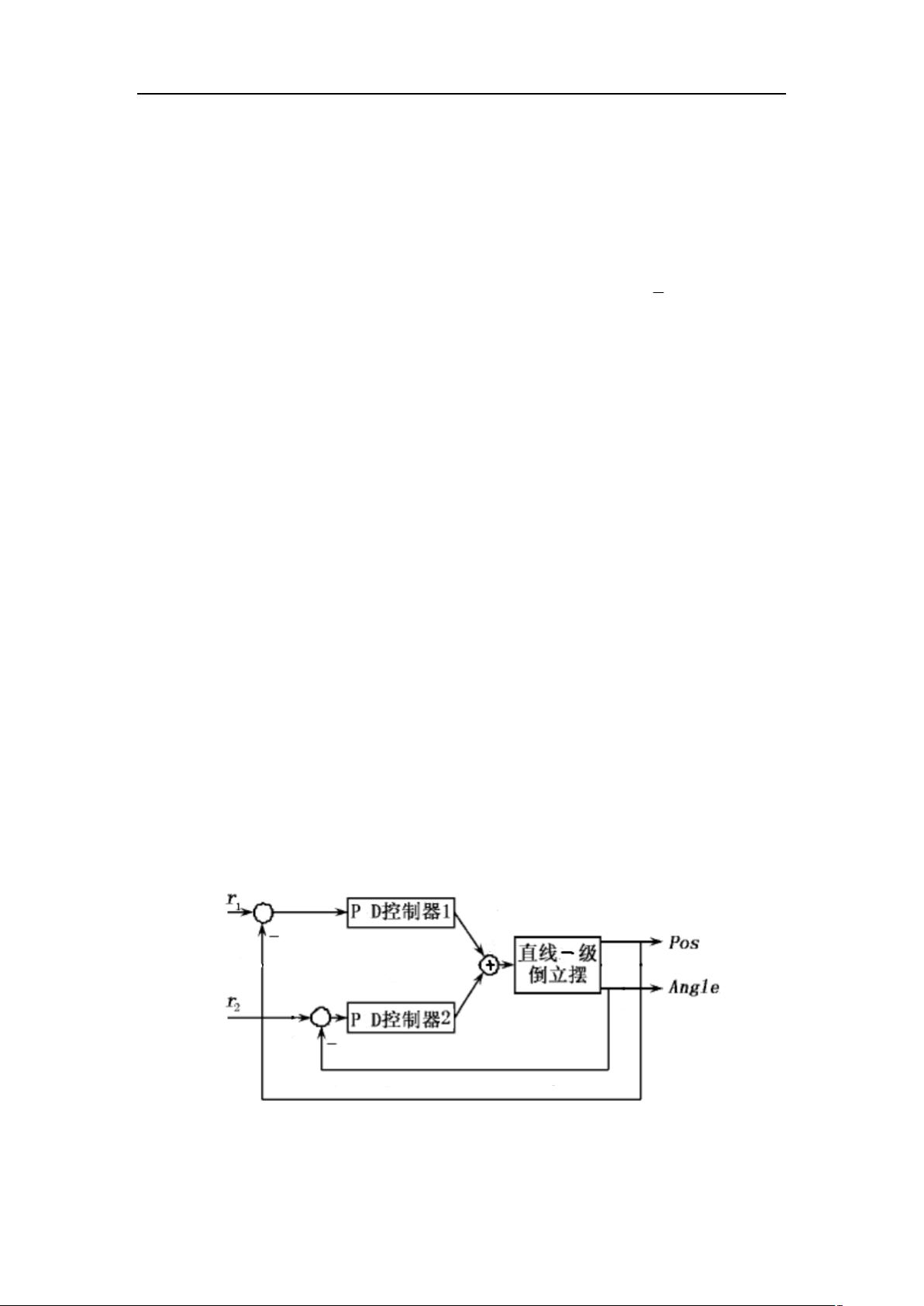
对于双路 PD 控制,控制周期为 0.025s,结构为:
图 1 双路 PID 控制结构图
对于参数的选择,自己设置不好,于是采用遗传算法的方式进行参数优化。适应度函数



















