基于环形抽样代理模型的结构可靠性分析方法.docx

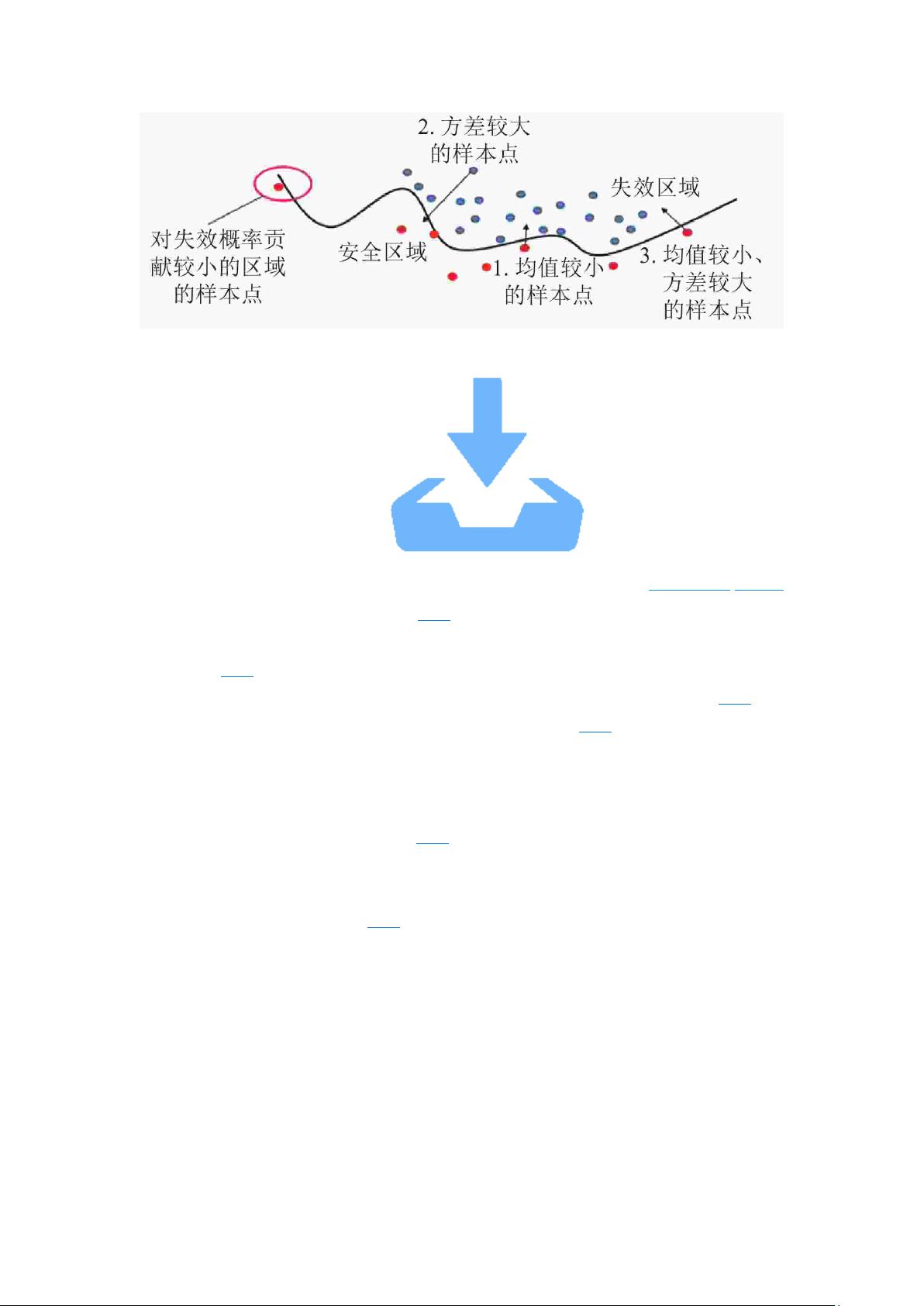
《基于环形抽样代理模型的结构可靠性分析方法》 结构可靠性分析是处理工程中不确定性问题的关键技术，尤其是在面临振动、冲击、加速度、噪声和载荷等因素影响时，准确评估结构性能和可靠性的能力至关重要。传统的蒙特卡洛仿真（MCS）方法虽然精度高，但对小概率事件的分析需要大量计算，效率低下。为了解决这一问题，第一阶和第二阶可靠性分析方法（FORM/SORM）被提出，通过泰勒展开近似性能函数。然而，对于高度非线性的性能函数，这些方法的精度受限。 近年来，代理模型技术成为提高结构可靠性分析效率的有效手段，其中Kriging模型因其精确的插值特性和对估计不确定性方差的考虑而受到广泛关注。Kriging模型是一种基于高斯过程回归的插值方法，可以估计响应的均值和不确定性。模型包括线性回归部分和随机过程部分，其数学表达式由多项式函数和随机过程组成。随机过程部分服从正态分布，相关函数通常选择高斯方程，以体现数据点间的关联性。 在Kriging模型的应用中，抽样区域的选择直接影响分析效率。传统的抽样策略可能会在对失效概率贡献较小的区域过度抽样，造成计算资源的浪费。因此，本文提出了一种基于3σ准则和欧式距离确定抽样区域的方法，旨在优化代理模型的更新过程，避免无效计算，提高分析效率。此外，调整抽样区域的带宽，也能适应小失效概率问题的解决。 文献中还提到了其他一些优化策略，如U方程、子集模拟、K-Means聚类算法和连接极限状态方程两侧样本点的方法，这些方法都在一定程度上提升了可靠性分析的效率，但在抽样区域问题上的关注较少。本文的研究填补了这一空白，为结构可靠性分析提供了更高效、更具针对性的解决方案。 总结来说，这篇文档探讨了如何利用Kriging代理模型和优化的抽样策略来提升结构可靠性分析的效率，特别是针对小概率失效事件的处理。通过合理确定抽样区域和调整带宽，可以有效减少计算资源的浪费，提高分析速度，对于实际工程问题的解决具有重要的理论与实践意义。