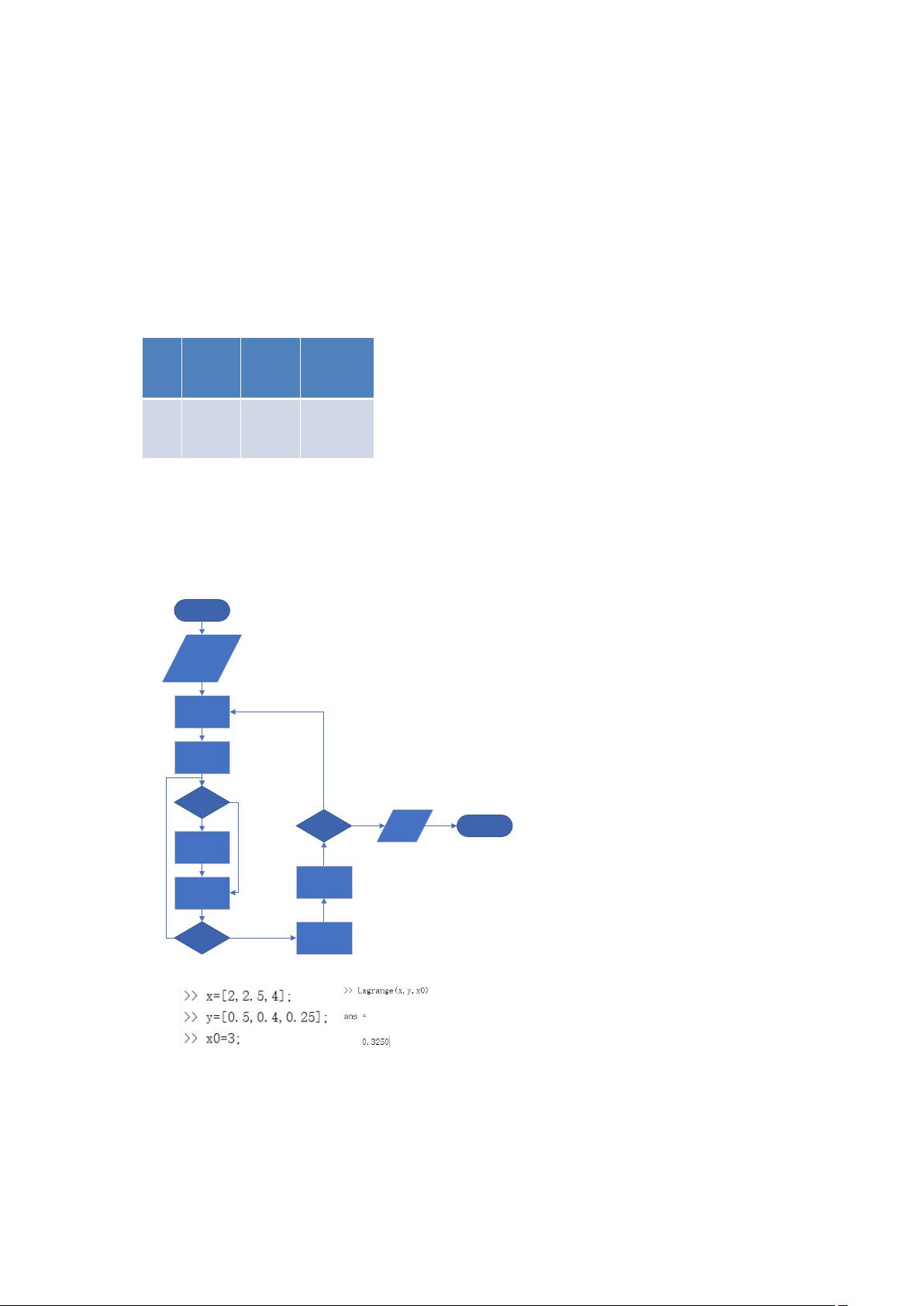
**Lagrange插值实验报告**
Lagrange插值是一种在离散数据点上构建多项式函数的方法，常用于数值分析和数据拟合。在MATLAB中，我们可以编写M文件来实现这一算法，以找到未知点上的函数近似值。
**实验程序功能**
Lagrange插值函数`Lagrange(x,y,x0)`接受三个参数：`x`是已知的插值点数组，`y`是对应的函数值，`x0`是要求解的插值点的x值。该函数的目标是通过给定的数据点找到一个多项式，使得这个多项式在每个数据点上都与原函数相等，并返回在`x0`处的函数近似值。
**实验步骤**
1. 在MATLAB中创建一个M文件，定义Lagrange插值函数。这个函数通常包含一个循环，遍历所有数据点，计算每个Lagrange基多项式`L_i`，并将其与对应的函数值`y_i`相乘后累加得到最终的插值结果。
2. 实际应用Lagrange插值，例如求解`f(3)`的近似值，以及`f(1)`和`f(5)`，并分析结果的准确性。这可以通过在MATLAB环境中调用自定义的`Lagrange`函数完成。
3. 设计更复杂的测试，如假设函数`f(x) = xe`或`f(x) = x*ln(x)`。先用科学计算器计算几组数值，然后用Lagrange函数在特定点（如`x=2.5`）进行插值计算。比较两个结果的差异，计算相对误差以评估插值的精确度。
**Lagrange插值算法流程**
1. 输入数据点`X1, X2, ..., Xn`和对应的函数值`Y1, y2, ..., yn`，以及要求解的`x0`。
2. 初始化变量`L = 1`，`J = 0`。
3. 对于每个数据点`Xi`（`i = 0, 1, ..., n`），计算Lagrange基多项式`L_i`，并更新`L`和`J`。
- 如果`i`不等于`j`，则`L = L * (x0 - x(j)) / (x(i) - x(j))`。
- 更新`J`为`j+1`，直到`J <= n`。
4. 计算插值结果`y = f(x0) = L * Y_i`，其中`Y_i`是对应的`yi`值。
5. 输出插值结果`y`。
**程序运行情况**
实验中，我们使用了一组数据点`(2, 0.5), (2.5, 0.4), (4, 0.25)`，并求解了`f(3)`的近似值。此外，我们还测试了复杂函数`xe`，在`x=2.5`处，通过Lagrange插值得到的近似值与科学计算器计算的值存在约9.62%的相对误差。
**心得体会**
通过这次实验，我对Lagrange插值法有了深入的理解。了解到当插值点按升序排列，且要求解的`x0`在这些点之间时，插值结果更为准确。同时，由于Lagrange插值构造的多项式是固定的，对于非线性的函数，如`xe`，可能会导致插值精度下降。这强调了选择合适的插值方法和理解其适用条件的重要性。
