没有合适的资源?快使用搜索试试~ 我知道了~
广义表的基本操作与高级功能

试读
27页
需积分: 0 0 下载量 45 浏览量
更新于2024-11-16
收藏 472KB PDF 举报
这份资料详细介绍了广义表(Generalized List)这一重要的数据结构。广义表是一种递归数据结构,其元素可以是原子(基本数据类型,如数字、字符)或者子表(另一个广义表),具有灵活性和递归性的特点。
资料主要包含七个部分:基本概念介绍、表示方法、存储结构、基本操作、高级操作、应用场景和优化策略。在基本操作部分,详细讲解了创建、遍历、插入、删除等功能的具体实现,每个操作都配有完整的C语言代码示例。在应用场景部分,展示了广义表在表示嵌套表达式、树结构和多层嵌套数据等实际场景中的应用。针对实现过程中可能遇到的内存管理、递归效率、栈溢出等问题,资料也提供了相应的优化策略和解决方案。

⼴
义
表
⼀
、
⼴
义
表
的
基
本
概
念
1.
什么
是
⼴
义
表
1.1
⼴
义
表
的
定
义
⼴
义
表
(
GeneralizedList
)
是
⼀
种
递
归
数
据
结
构
,
它
的
每
个
元
素
可
以
是
原
⼦
(
不
可
再
分
的
基
本
数
据
类
型
,
如
字
符
、
数
字
等
)
或
另
⼀个
⼴
义
表
(
称
为
⼦
表
)
。
⼴
义
表
的
特
点
是
灵
活
性
和
递
归
性
,
能
够
表
⽰
多
层
嵌
套
的
数
据
结
构
。
⼴
义
表
可
以
通过
以
下
⽅
式
定
义
:
1.
⼀个
空
表
是
⼴
义
表
,
⽤
()
表
⽰
。
2.
⼀个
⾮
空
表
由
表
头
和
表
尾
组
成
,
表
头
是
⼀个
元
素
(
原
⼦
或
另
⼀个
⼴
义
表
),
表
尾
是
⼀个
⼴
义
表
。
⽰
例
:
•
空
表
:
()
•
单
层
⼴
义
表
:
(a, b, c)
•
嵌
套
⼴
义
表
:
(a, b, (c, d))
1.2
⼴
义
表
的
核
⼼
特
性
递
归
性
:
⼴
义
表
由
⾃
⾝
定
义
,
其
⼦
表
也
是
⼴
义
表
。
灵
活
性
:
⼴
义
表
可
以
动
态
扩
展
,
⽀
持
多
层
嵌
套
,
适
⽤
于
复
杂
的
数
据
描
述
。
动
态性
:
⼴
义
表
的
深
度
和
元
素
数
量
不
固
定
,
结
构
可
以
灵
活
调
整
。
2.
⼴
义
表
与
线
性
表
的
区
别
2.1
元
素
类
型
的
区
别
线
性
表
的
元
素
只
能
是
原
⼦
类
型
,
如
数
字
、
字
符
,
⽽
⼴
义
表
的
元
素
既
可
以
是
原
⼦
,
也
可
以
是
⼦
表
(
即
⼴
义
表
⾃
⾝
)
。
2.2
表
结
构
的
层
次
性
⽐
较
线
性
表
是
单
层
结
构
,
所
有
元
素
在
⼀个
层
级
中
。
⽽
⼴
义
表
⽀
持
多
层
嵌
套
,
⼦
表
的
层
次
可
以
⽆
限
递
归
。
2.3
存
储
⽅
式
的
不
同

线
性
表
通
常
⽤
数
组
或
链
表
存
储
。
⽽
⼴
义
表
需
要
链
表
的
扩
展
形式
,
每
个
节
点
存
储
表
头
的
内
容
,
同
时
指
向
表
尾
,
表
尾
⼜
可
以
是
另
⼀个
⼦
表
。
3.
⼴
义
表
的
应
⽤
场
景
3.1
编
译
原
理
中
的
语
法
树
表
⽰
在
编
译
器
中
,
⼴
义
表
常
⽤
于
表
⽰
语
法
树
(
SyntaxTree
)
或抽
象语
法
树
(
AbstractSyntaxTree,
AST
)
。
例
如
,
表
达
式
1 + (2 * 3)
可
以
⽤
⼴
义
表表
⽰
为
(+, 1, (*, 2, 3))
,
这
种
结
构
清
晰
地
展
⽰
了
运
算
的
优
先
级
和
嵌
套
关
系
。
3.2
数
据
交
换
中
的
嵌
套
结
构
⼴
义
表
可
以
表
⽰
JSON
和
XML
等
嵌
套
数
据
结
构
。
例
如
,
JSON
对
象
{"name": "Alice",
"scores": [90, 85]}
可
以
⽤
⼴
义
表表
⽰
为
(name, Alice, (scores, 90, 85))
,
⾮
常
直
观
。
3.3
算
法
与
数
据
结
构
教
学
⼴
义
表
是
递
归
数
据
结
构
的
经
典
案
例
,
适
合
⽤
于
教
学
递
归
算
法
、
树
形
结
构
,
以
及
链
表
等
基
本
数
据
结
构
的
概
念
。
⽰
例代
码
以
下
⽤
C
语
⾔
实
现
了
⼴
义
表
的
基
本
数
据
结
构
和
打
印
功
能
:
#include <stdio.h>
#include <stdlib.h>
//
定
义
⼴
义
表
节
点
类
型
typedef enum { ATOM, LIST } NodeType;
//
定
义
⼴
义
表
节
点
结
构
typedef struct Node {
NodeType type;
//
节
点
类
型
:
原
⼦
或
⼦
表
union {
char data;
//
原
⼦
元
素
struct Node *subList;
//
⼦
表
指
针
};
struct Node *next;
//
指
向
下⼀个
节
点
} Node;
//
创
建
原
⼦
节
点
Node *createAtom(char data) {
Node *node = (Node *)malloc(sizeof(Node));
node->type = ATOM;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

node->data = data;
node->next = NULL;
return node;
}
//
创
建
⼦
表
节
点
Node *createSubList(Node *subList) {
Node *node = (Node *)malloc(sizeof(Node));
node->type = LIST;
node->subList = subList;
node->next = NULL;
return node;
}
//
打
印
⼴
义
表
void printGeneralizedList(Node *list) {
printf("(");
while (list != NULL) {
if (list->type == ATOM) {
printf("%c", list->data);
} else if (list->type == LIST) {
printGeneralizedList(list->subList);
}
if (list->next != NULL) {
printf(", ");
}
list = list->next;
}
printf(")");
}
//
⽰
例使
⽤
int main() {
//
创
建
原
⼦
节
点
Node *a = createAtom('a');
Node *b = createAtom('b');
//
创
建
⼦
表
(c, d)
Node *c = createAtom('c');
Node *d = createAtom('d');
c->next = d;
//
链
接
⼦
表
节
点
Node *subList = createSubList(c);
//
构
造
⼴
义
表
(a, b, (c, d))
a->next = b;
b->next = subList;
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
//
打
印
⼴
义
表
printf("
⼴
义
表
内
容
:
");
printGeneralizedList(a);
printf("\n");
//
释
放
内
存
(
简
化
处
理
,
实
际
应
递
归
释
放
所
有
节
点
)
free(a);
free(b);
free(c);
free(d);
free(subList);
return 0;
}
68
69
70
71
72
73
74
75
76
77
78
79
80
81
运
⾏
结
果
:
⼴
义
表
内
容
:
(a, b, (c, d))
1
⼆
、
⼴
义
表
的
表
⽰
⽅
法
1.
数
学
表
⽰
法
数
学
表
⽰
法
是
⼴
义
表
的
理
论
基
础
,
使
⽤
集
合
论
的
概
念
来
描
述
⼴
义
表
的
递
归
定
义
。
⼴
义
表
可
以
通过
以
下
⽅
式
描
述
:
1.
空
表
⽤
∅
或
{}
表
⽰
。
2.
⾮
空
表
由
两个
部
分
组
成
:
表
头
和
表
尾
,
表
头
可
以
是
原
⼦
或
另
⼀个
⼴
义
表
,
表
尾
是
⼀个
⼴
义
表
。
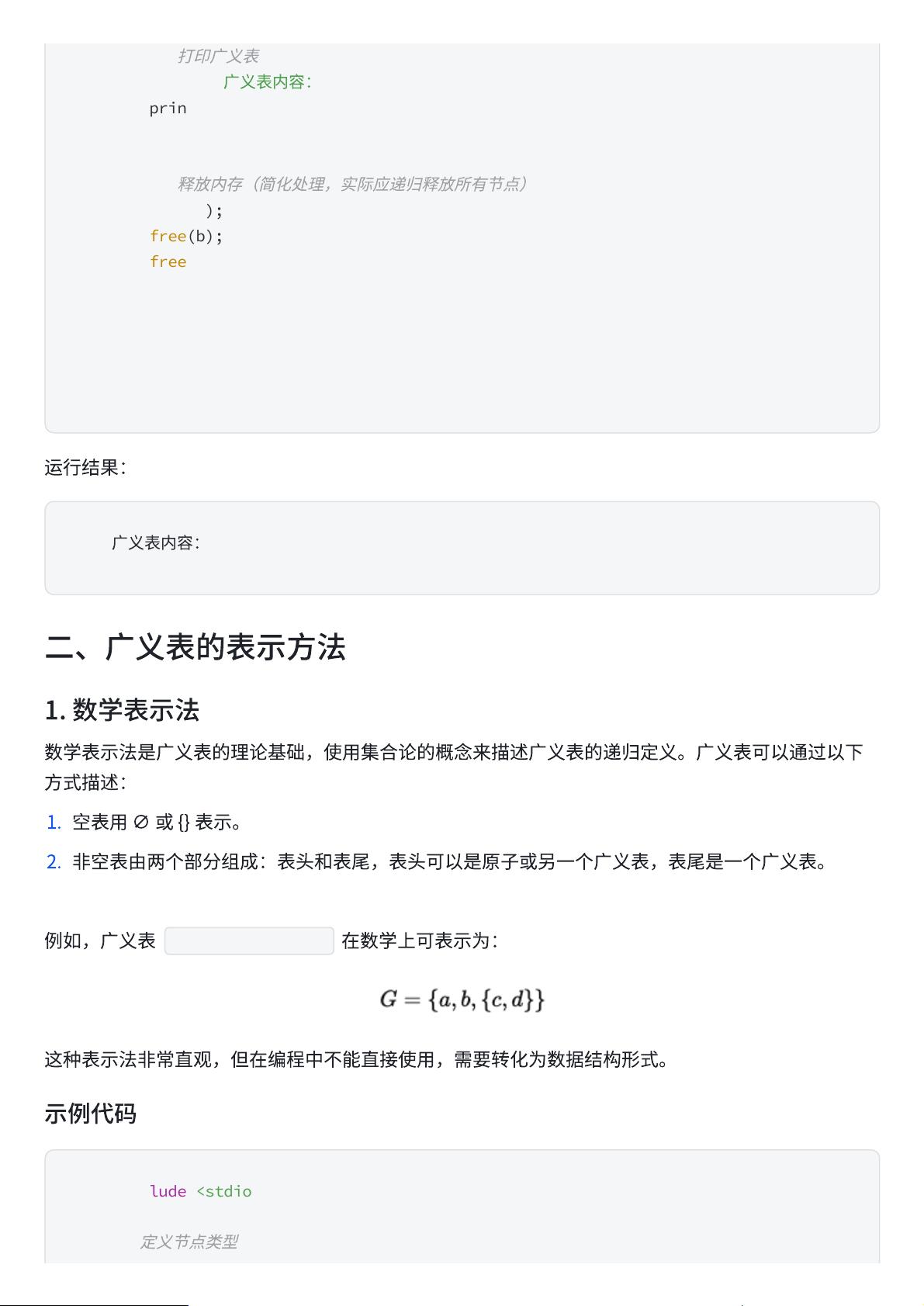
例
如
,
⼴
义
表
(a, b, (c, d))
在
数
学
上
可
表
⽰
为
:
这
种
表
⽰
法
⾮
常
直
观
,
但
在
编
程
中不
能
直
接
使
⽤
,
需
要
转
化
为
数
据
结
构
形式
。
⽰
例代
码
#include <stdio.h>
//
定
义
节
点
类
型
1
2
3

typedef enum { ATOM, LIST } NodeType;
//
定
义
节
点
结
构
typedef struct Node {
NodeType type;
union {
char data;
//
如
果
是
原
⼦
,
存
储
数
据
struct Node *subList;
//
如
果
是
⼦
表
,
指
向另
⼀个
表
};
struct Node *next;
//
指
向
下⼀个
节
点
} Node;
4
5
6
7
8
9
10
11
12
13
14
上
⾯
的
代
码
展
⽰
了
如
何
通过
C
语
⾔
定
义
数
据
结
构
,
来
将
数
学定
义
转
化
为
计
算
机
表
⽰
形式
。
2.
图
形
表
⽰
法
图
形
表
⽰
法
是
⼴
义
表
的
⼀
种
直
观
表
达
⽅
式
,
通
常
使
⽤
树
状
结
构来
描
述
表
的
嵌
套
关
系
。
每
个
节
点
可
以
是
⼀个
原
⼦
(
叶
⼦
节
点
)
或
⼀个
⼦
表
(
⾮
叶
⼦
节
点
)
。
例
如
,
⼴
义
表
(a, b, (c, d))
的
图
形
表
⽰
如
下
:
G
/|\
a b subList
/ \
c d
1
2
3
4
5
在
树
状
表
⽰
中
,
原
⼦
表
⽰
叶
⼦
节
点
,
⼦
表
通过
分
⽀
递
归
连
接
。
⽰
例代
码
#include <stdio.h>
//
打
印
图
形
化
表
⽰
法
(
模
拟
)
void printTreeRepresentation() {
printf("
⼴
义
表
的
图
形
表
⽰
:
\n");
printf(" G\n");
printf(" /|\\\n");
printf(" a b subList\n");
printf(" / \\\n");
printf(" c d\n");
}
int main() {
1
2
3
4
5
6
7
8
9
10
11
12
13
剩余26页未读,继续阅读
资源推荐
资源评论
2019-12-02 上传
113 浏览量
2024-01-10 上传
175 浏览量
133 浏览量
119 浏览量
176 浏览量
2021-10-20 上传
183 浏览量
2009-09-20 上传
160 浏览量
190 浏览量
130 浏览量
2008-03-10 上传
133 浏览量
2021-09-28 上传
181 浏览量
2013-07-02 上传
191 浏览量
2024-03-11 上传
160 浏览量
2011-12-18 上传
2010-06-17 上传
177 浏览量
资源评论

程序媛学姐
- 粉丝: 809
- 资源: 5
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功