比特数据结构课件-Lesson6-排序.pdf

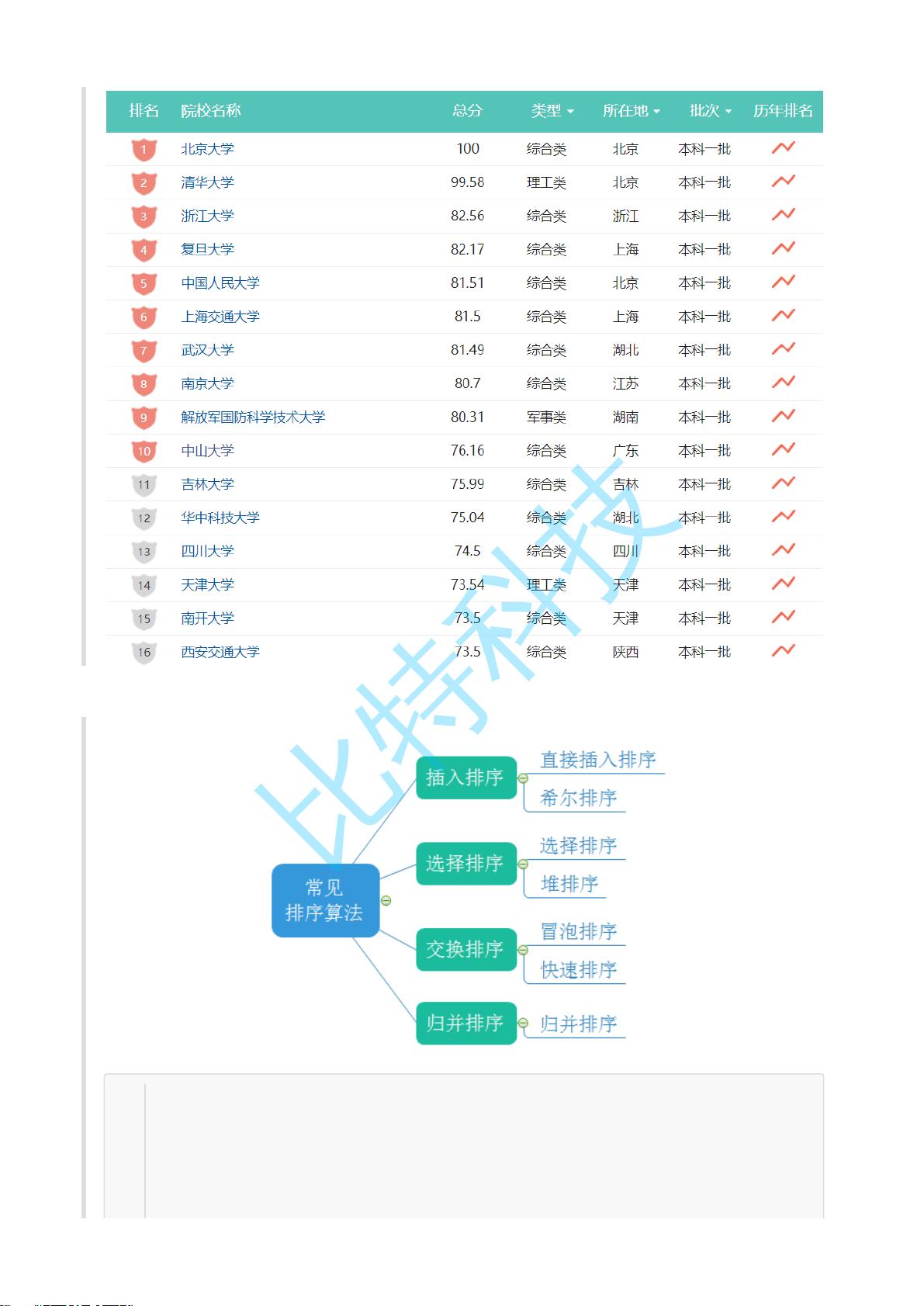
【排序算法详解】 排序是计算机科学中一个基础且重要的概念，它涉及到对一组数据进行有特定顺序的组织。在比特数据结构课件的Lesson6中，主要探讨了排序的定义、分类以及常见的排序算法实现，并通过性能对比来展示不同算法的效率。 1. **排序的概念及其运用** - **排序概念**：排序是指根据特定的关键字（如数值或字符串）对一系列数据进行升序或降序排列的过程。 - **稳定性**：稳定排序算法保证相等的元素在排序后保持原有的相对顺序，而不稳定排序则不保证这一点。 - **内部排序与外部排序**：内部排序适用于数据量小到可以一次性装入内存的情况，而外部排序则用于处理数据量过大无法一次性装入内存的场景，通常需要多次磁盘读写操作。 2. **常见排序算法** - **插入排序**：插入排序是一种简单的排序方法，它将每个元素插入到已排序的部分，依次构建整个有序序列。直接插入排序的时间复杂度为O(n^2)。 - **希尔排序**：希尔排序是插入排序的一种改进版，通过增量序列将待排序数组分组，然后对各组进行插入排序，最终达到快速排序的效果。 - **选择排序**：每次从未排序部分选择最小（或最大）元素放到已排序部分的末尾，时间复杂度为O(n^2)。 - **堆排序**：利用二叉堆结构，将数组转换成堆，然后交换堆顶元素和末尾元素，再调整堆，最后达到排序目的，时间复杂度为O(n log n)。 - **冒泡排序**：相邻元素两两比较，如果顺序错误就交换，多次迭代直到排序完成，时间复杂度为O(n^2)。 - **快速排序**：采用分治策略，通过一次划分操作将数组分为两个子数组，然后递归地对子数组进行排序，平均时间复杂度为O(n log n)，最坏情况下为O(n^2)。 - **归并排序**：将数组分成两半，分别排序后再合并，保证了稳定性，时间复杂度始终为O(n log n)。 3. **排序算法复杂度及稳定性分析** - 时间复杂度是衡量排序算法效率的重要指标，如上述所述，不同算法在不同情况下的表现各有优劣。 - 稳定性则关系到排序结果中相同元素的相对位置是否保持不变，对于某些应用场景，如统计学或数据库操作，稳定性至关重要。 4. **排序算法的实现** - 课件中提供了多种排序算法的C语言实现，包括插入排序、希尔排序、选择排序、堆排序、冒泡排序、快速排序（包括Hoare版本、挖坑法、前后指针法）、归并排序（递归和非递归实现）以及计数排序。这些实现可以作为学习和理解排序算法的基础代码。 5. **测试排序的性能对比** - 对比不同排序算法的性能是评估它们实际应用价值的关键步骤。课件中提供的`TestOP`函数使用随机生成的数据，对各种排序算法进行计时，从而直观地看出各种算法在相同条件下的速度差异。 6. **在线实践平台** - 课件还提到了一个排序算法在线实践平台（OJ），可以用来测试和运行各种排序算法，这为学习者提供了实战环境，有助于深化理解和提高编程技能。 通过深入学习这些排序算法，不仅可以掌握排序的基本原理，还能提升解决实际问题的能力。不同的排序算法各有特点，适用场景也不同，理解并灵活运用这些算法，能有效提高编程效率和软件性能。