深度学习之六:机器学习原理之 logistic 回归算法与代码实现
Logistic 回归算法原理与代码实现
本文系作者原创,转载请注明出
处:https://www.cnblogs.com/further-further-further/p/10033567.html
主要思想
根据现有数据对分类边界线建立回归公式,以此进行分类,其核心是通过最优化算法寻找最佳回
归系数(权重系数),主要应用于二分类。
算法原理
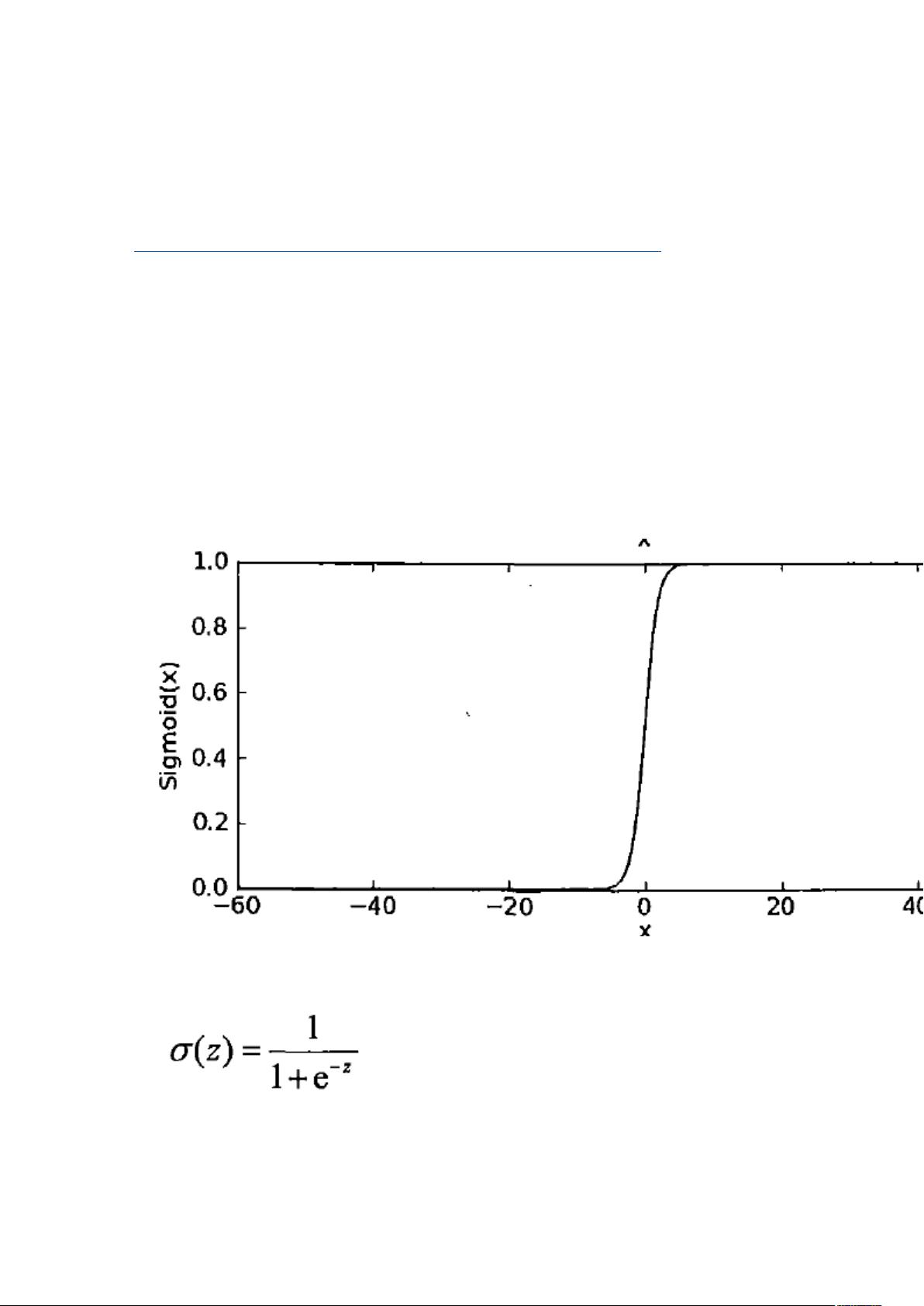
二分类的特点是非此即彼,其数学特性符合单位阶跃函数,在某一点会发生突变。这也符合我
们现实当中的一些应用场景(比如分数从 0 到 60 会很容易,越往上你所花的时间精力就越大,也就越
难)。
Sigmoid 函数的计算公式如下
算法步骤

1. 初始化回归系数(权重系数),以 Sigmoid 作为分类函数;
2. 构造代价函数(损失函数),用以表示目标结果与预测结果的差值;
3. 重复迭代,找到最小代价函数,获取最佳回归系数(权重系数);
4. 预测测试数据结果,计算平均差错率;
代码理解
在机器学习实战关于 logistic 实现的代码中,我个人认为代码可读性不怎么好,没有很好的区分
list,array,matrix,
甚至有些字段命名容易造成误解。
list,array,matrix 区别:
1. list 是不能直接进行数学运算,必须转化为 array 或者 matrix;
2. matrix 比 array 多一维,取值方式[ , ] 例如[0,0];
3. 含有 matrix 类型的运算,数组会强制转化为矩阵,按照矩阵运算法则进行运算,所得结果类
型是矩阵;
4. 数组乘法下标必须完全一样,矩阵乘法必须符合 m * n n* k;
我将代码进行了一些修改,后缀可以很清楚数据类型(_list :list _arr:array _mat:
matrix)
代码实现(Spyder Python3.6)
我已将每个方法添加注释,并将字段名做了修改,因为数组和矩阵运算规则完全不一样,字段名
如果很清晰的看出数据类型,对于理解代码背后的思想,
应该会有一些帮助。
testSet.txt
-0.017612 14.053064 0
-1.395634 4.662541 1
-0.752157 6.538620 0
-1.322371 7.152853 0
0.423363 11.054677 0
0.406704 7.067335 1
0.667394 12.741452 0
-2.460150 6.866805 1
0.569411 9.548755 0
-0.026632 10.427743 0
0.850433 6.920334 1
1.347183 13.175500 0

1.176813 3.167020 1
-1.781871 9.097953 0
-0.566606 5.749003 1
0.931635 1.589505 1
-0.024205 6.151823 1
-0.036453 2.690988 1
-0.196949 0.444165 1
1.014459 5.754399 1
1.985298 3.230619 1
-1.693453 -0.557540 1
-0.576525 11.778922 0
-0.346811 -1.678730 1
-2.124484 2.672471 1
1.217916 9.597015 0
-0.733928 9.098687 0
-3.642001 -1.618087 1
0.315985 3.523953 1
1.416614 9.619232 0
-0.386323 3.989286 1
0.556921 8.294984 1
1.224863 11.587360 0
-1.347803 -2.406051 1
1.196604 4.951851 1
0.275221 9.543647 0
0.470575 9.332488 0
-1.889567 9.542662 0
-1.527893 12.150579 0
-1.185247 11.309318 0
-0.445678 3.297303 1
1.042222 6.105155 1
-0.618787 10.320986 0
1.152083 0.548467 1
0.828534 2.676045 1
-1.237728 10.549033 0
-0.683565 -2.166125 1
0.229456 5.921938 1
-0.959885 11.555336 0
0.492911 10.993324 0
0.184992 8.721488 0
-0.355715 10.325976 0
-0.397822 8.058397 0
0.824839 13.730343 0
1.507278 5.027866 1
0.099671 6.835839 1

-0.344008 10.717485 0
1.785928 7.718645 1
-0.918801 11.560217 0
-0.364009 4.747300 1
-0.841722 4.119083 1
0.490426 1.960539 1
-0.007194 9.075792 0
0.356107 12.447863 0
0.342578 12.281162 0
-0.810823 -1.466018 1
2.530777 6.476801 1
1.296683 11.607559 0
0.475487 12.040035 0
-0.783277 11.009725 0
0.074798 11.023650 0
-1.337472 0.468339 1
-0.102781 13.763651 0
-0.147324 2.874846 1
0.518389 9.887035 0
1.015399 7.571882 0
-1.658086 -0.027255 1
1.319944 2.171228 1
2.056216 5.019981 1
-0.851633 4.375691 1
-1.510047 6.061992 0
-1.076637 -3.181888 1
1.821096 10.283990 0
3.010150 8.401766 1
-1.099458 1.688274 1
-0.834872 -1.733869 1
-0.846637 3.849075 1
1.400102 12.628781 0
1.752842 5.468166 1
0.078557 0.059736 1
0.089392 -0.715300 1
1.825662 12.693808 0
0.197445 9.744638 0
0.126117 0.922311 1
-0.679797 1.220530 1
0.677983 2.556666 1
0.761349 10.693862 0
-2.168791 0.143632 1
1.388610 9.341997 0
0.317029 14.739025 0

训练数据
horseColicTraining2.txt
2.000000 1.000000 38.500000 66.000000 28.000000 3.000000 3.000000
0.000000 2.000000 5.000000 4.000000 4.000000 0.000000 0.000000
0.000000 3.000000 5.000000 45.000000 8.400000 0.000000 0.000000
0.000000
1.000000 1.000000 39.200000 88.000000 20.000000 0.000000 0.000000
4.000000 1.000000 3.000000 4.000000 2.000000 0.000000 0.000000
0.000000 4.000000 2.000000 50.000000 85.000000 2.000000 2.000000
0.000000
2.000000 1.000000 38.300000 40.000000 24.000000 1.000000 1.000000
3.000000 1.000000 3.000000 3.000000 1.000000 0.000000 0.000000
0.000000 1.000000 1.000000 33.000000 6.700000 0.000000 0.000000
1.000000
1.000000 9.000000 39.100000 164.000000 84.000000 4.000000 1.000000
6.000000 2.000000 2.000000 4.000000 4.000000 1.000000 2.000000
5.000000 3.000000 0.000000 48.000000 7.200000 3.000000 5.300000
0.000000
2.000000 1.000000 37.300000 104.000000 35.000000 0.000000 0.000000
6.000000 2.000000 0.000000 0.000000 0.000000 0.000000 0.000000
0.000000 0.000000 0.000000 74.000000 7.400000 0.000000 0.000000
0.000000
2.000000 1.000000 0.000000 0.000000 0.000000 2.000000 1.000000
3.000000 1.000000 2.000000 3.000000 2.000000 2.000000 1.000000
0.000000 3.000000 3.000000 0.000000 0.000000 0.000000 0.000000
1.000000
1.000000 1.000000 37.900000 48.000000 16.000000 1.000000 1.000000
1.000000 1.000000 3.000000 3.000000 3.000000 1.000000 1.000000
0.000000 3.000000 5.000000 37.000000 7.000000 0.000000 0.000000
1.000000
1.000000 1.000000 0.000000 60.000000 0.000000 3.000000 0.000000
0.000000 1.000000 0.000000 4.000000 2.000000 2.000000 1.000000
0.000000 3.000000 4.000000 44.000000 8.300000 0.000000 0.000000
0.000000
2.000000 1.000000 0.000000 80.000000 36.000000 3.000000 4.000000
3.000000 1.000000 4.000000 4.000000 4.000000 2.000000 1.000000
0.000000 3.000000 5.000000 38.000000 6.200000 0.000000 0.000000
0.000000
2.000000 9.000000 38.300000 90.000000 0.000000 1.000000 0.000000
1.000000 1.000000 5.000000 3.000000 1.000000 2.000000 1.000000



















