一、共轭梯度法求解线性方程组
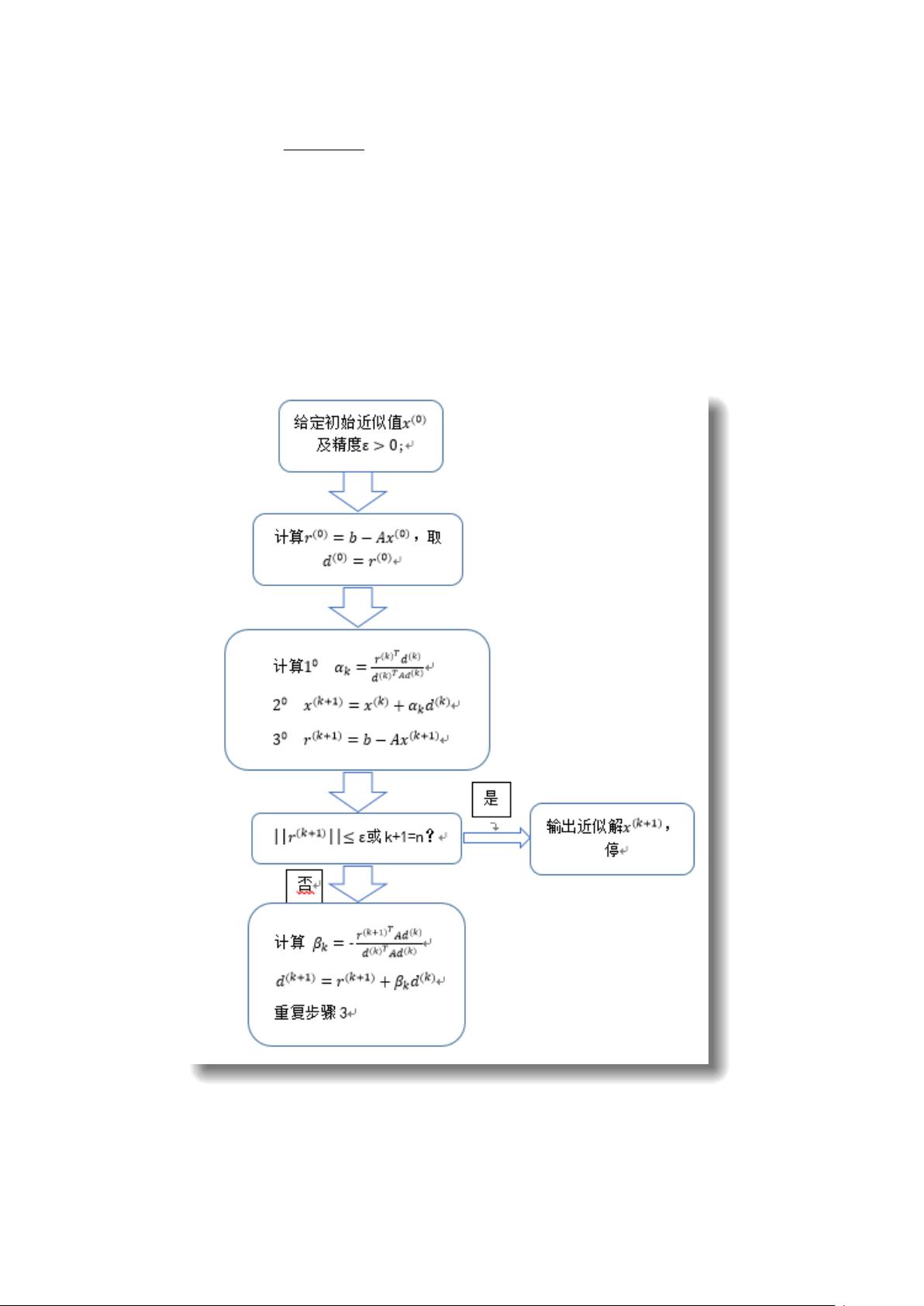
1. 算法原理及程序框图
共轭梯度法是把求解线性方程组的问题转化为求解一个与之等价的二次函数极小化问
题,从任意给定的初始点出发,沿一组关于矩阵 A 的共轭方向进行线性搜索,在无摄入误
差的假设下,最多迭代 n 次,就可以求得二次函数的极小点。也就是求的了线性方程组 Ax=B
的解。
定理 3-4-1 设 A 是 n 阶对称正定矩阵,则 x*是方程组 Ax=b 的解的充分必要条件是 x*
是二次函数
f(x)
=
1
2
𝑥
𝑇
𝐴𝑥
―
𝑏
𝑇
𝑥
的较小点,即
A
𝑥
∗
=
𝑏
𝑓(
𝑥
∗
)
=
min
𝑥
∈
𝑅
𝑛
𝑓(𝑥)
定义 3-4-1(共轭向量)设 A 是 n 阶对称正定矩阵,若中的一组非零向量 d (0) , d
(1 ) , · · · , d (m )满足(d (i) , Ad (j )) = 0 ,
i
≠
j
, 则称 d (i ) , d (j )是关于 A 的共轭向量,d (0) , d
(1) , · · · , d (m )是关于矩阵 A 的共轭向量组。
定理 3-4-2 关于矩阵 A 的共轭向量 d (0) , d (1) , · · · , d ( m ),线性无关。
共轭梯度法在形式上具有迭代法的特征,给定初始向量,由迭代格式产生的序列 x(1) ,
x(2) , x(3) , · · · ,求得 f(x)的最小点,也就是方程组 Ax=b 的解。共轭梯度法中关键的两点
是,确定迭代格式中的搜索向量 d( k)和最佳步长 α
k
( α
k
≥ 0)。
步长 α
k
的确定原则是给定迭代点 x ( k)和和搜索方向后 d( k),要求选择非负实数 αk 使
得 f(x( k) + α
k
d( k))达到最小。即选择满足 f(x( k) + α
k
d( k)) = min f(x(k) + αd( k))。
共轭梯度法的计算过程:
(1)给定初始近似点 x (0)及精度
0
e
>
;
(2)计算 r (0) = b − Ax (0),取 d (0) = r (0);
(3)for k = 0 to n − 1 do
(i)
( ) ( )
( ) ( )
k T k
k
k T k
r r
d Ad
a
=
;
(i) x
(k+1)
= x
(k)
+ α
k
d
(k)
;
(iii) r
(k+1)
= b − Ax
(k+1)
;
(iv) 若
( 1)
| ||
k
r
e
+
£
或 k+1=n,则输出近似解 x
(k+1)
,停止;否则转(v);