Figure 1: Transparentencryption in the “trusted databasesoft-
ware with vulnerable storage” setting.
encrypted value
c
; a breach may occur if the adversary succeeds
in obtaining a tight estimate of
p
. For a numeric domain
P
,if
an adversary can estimate with
c
%
confidence that a data value
p
lies within the interval
[
p
1
;p
2
] then the interval width
(
p
2
,
p
1
)
=
domain-width
(
P
)
defines the amount of estimation exposure
at
c
%
confidence level.
Clearly, any order-preserving encryption scheme is vulnerable
to tight estimation exposure if the adversary can choose any num-
ber of unencrypted (encrypted) values of his liking and encrypt
(decrypt) them into their corresponding encrypted (unencrypted)
values. Similarly, any order-preserving encryption is not secure
against tight estimation exposure if the adversary canguess the do-
main and knows the distribution of values in that domain.
We consider an application environmentwhere the goal is safety
from an adversary who has access to all (but only) encryptedvalues
(the so called ciphertext only attack [22] [24]), and does not have
any special information about the domain. We will particularly fo-
cus on robustness against estimation exposure.
1.2 Threat Model
We assume (see Figure 1):
The storage system usedby the database softwareis vulnera-
ble to compromise. While current database systems typically
perform their own storage management, the storage system
remains part of the operating system. Attacks against storage
could be performed by accessing database files following a
path other than through the database software, or in the ex-
treme, by physical removal of the storage media.
The database software is trusted. We trust the database
software to transform query constants into their encrypted
values and decrypt the query results. Similarly, we assume
that an adversary does not have access to the values in the
memory of the database software.
All disk-resident data is encrypted. In addition to the data
values, the database software also encrypts schema infor-
mation such as table and column names, metadata such as
column statistics, as well as values written to recovery logs.
Otherwise, an adversary may be able to use this information
to guess data distributions.
1.3 Pedagogical Assumptions and Notations
The focus of this paper is on developing order-preserving en-
cryption techniques for numeric values and assumes conventional
encryption [22] [24] for other data types as well as for encrypting
information such as schema names and metadata. We will some-
time refer to unencrypted data values as plaintext. Similarly, en-
crypted values will also be referred to as ciphertext.
We will assume that the databaseconsists of a single table, which
in turn consists of a single column. The domain of the column will
be initially assumed to be a subset of integer values,
[
p
min
;p
max
)
.
The extension for real values is given later in the paper.
Assume the database
~
P
consists of a total of
j
~
P
j
plaintext values.
Out of these,
j
P
j
values are unique, which will be represented as
P
=
p
1
;p
2
;::: ;p
j
P
j
,
p
i
<p
i
+1
The corresponding encrypted
values will be represented as
C
=
c
1
;c
2
;::: ;c
j
P
j
,
c
i
<c
i
+1
.
Duplicates can sometimes be used to guess the distribution of a
domain, particularly if the distribution is highly skewed. A closely
related problem is that if the number of distinct values is small (e.g.,
day of the month), it is easy to guess the domain. We will ini-
tially assume that the domain to be encrypted either does not con-
tain many duplicates or contains a distribution that can withstand a
duplicate attack, and discuss the handling of duplicates later in the
paper.
1.4 Paper Layout
The rest of the paper is organized as follows. We first discuss re-
lated work in Section 2. We give an overview of OPES in Section 3.
The next three sections give details of the three main phases of
OPES. We describe extensions to handle real values and duplicates
in Section 7. In Section 8, we study the quality of the encryption
produced by OPES and present performance measurements from a
DB2 implementation. We conclude with a summary and directions
for future work in Section 9.
2. RELATED WORK
Summation of Random Numbers A simple scheme has been
proposed in [3] that computes the encrypted value
c
of integer
p
as
c
=
P
p
j
=0
R
j
,where
R
j
is the
j
th value generated by a se-
cure pseudo-random number generator
R
. Unfortunately, the cost
of making
p
calls to
R
for encrypting or decrypting
c
can be pro-
hibitive for large values of
p
.
A more serious problem is the vulnerability to estimation ex-
posure. Since the expected gap between two encrypted values is
proportional to the gap between the corresponding plaintext val-
ues, the nature of the plaintext distribution can be inferred from the
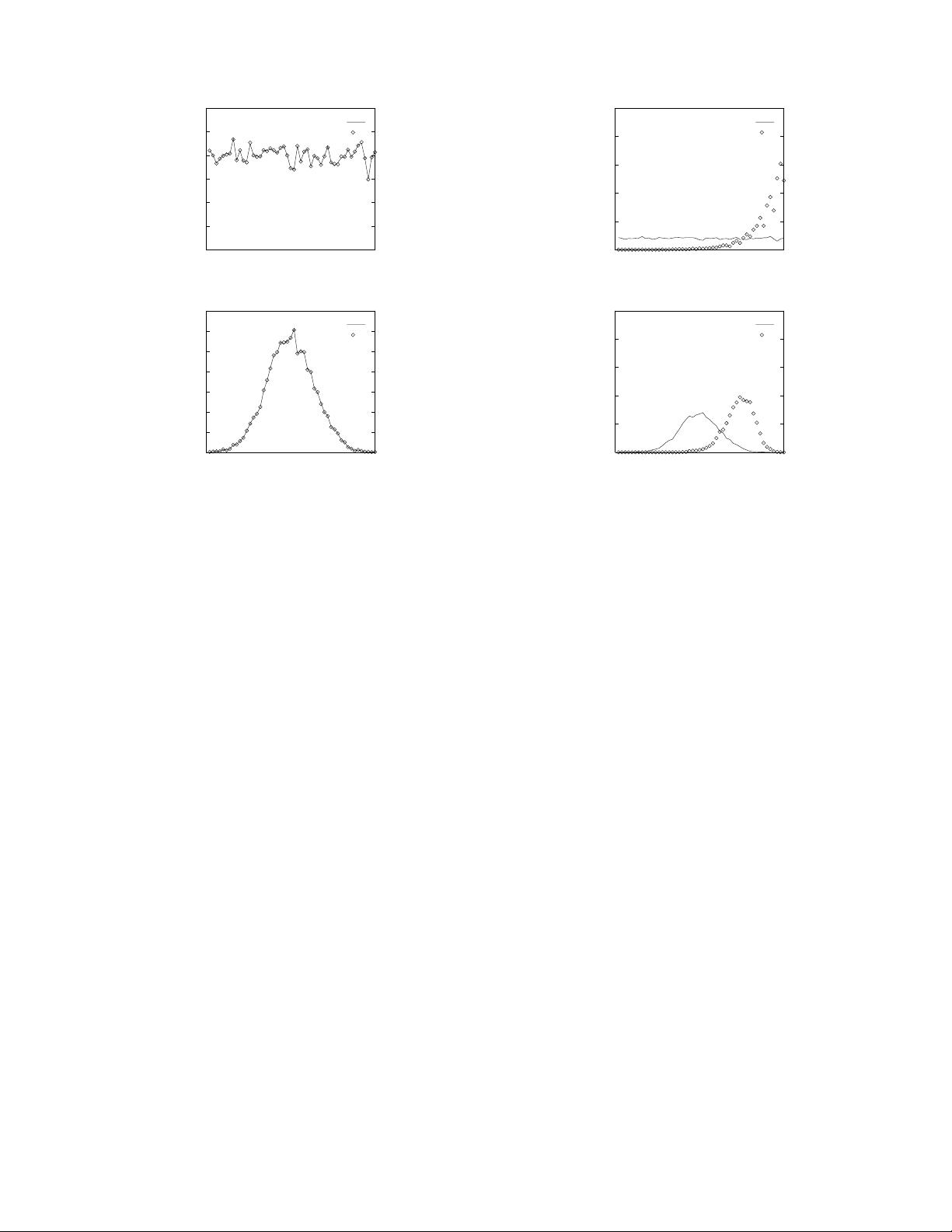
encrypted values. Figure 2 showsthe distributions of encryptedval-
ues obtained using this scheme for data values sampled from two
different distributions: Uniform and Gaussian. In each case, once
both the input and encrypted distributions are scaled to be between
0 and 1, the number of points in each bucket is almost identical for
the plaintext and encrypted distributions. Thus the percentile of a
point in the encrypted distribution is also identical to its percentile
in the plaintext distribution.


 opes.rar (1个子文件)
opes.rar (1个子文件)  opes.pdf 160KB
opes.pdf 160KB

 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助 
 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜

 信息提交成功
信息提交成功