
3D 游戏程序设计入门
(DirectX® 9.0)
翁云兵
四川·成都
二○○六年六月二十一日

前言
声明
z 本教程内容绝大部分来自 Frank D. Luna 所著的《Introduction to
3D Game Programming with DirectX 9.0》。教程内容(特别是语言
表达上)大部分是我根据自己理解所写的,因此也不全是此书的中
文翻译版。
z 由于我的英文水平很差,翻译过来就难免有错,望读者原谅。当然
如你认为我的水平实在是让人无法忍受那么请直接查阅英文教程。
z 此中文教程版权归我所有。
z 非商业应用可免费使用本教程。商业应用请同作者联系。
特别感谢
z www.GameRes.com是它让我走上了游戏开发的道路。
z Frank D. Luna 所著的《Introduction to 3D Game Programming with
DirectX 9.0》
z 一直关心、支持我的同事、同学以及 GameRes 上的所有读者。
z 我最最亲爱的老婆,没有她我不可能写出这本教程。
后续版本
该版本是发布的第一个完全版本。书中内容已经做过一次全面校对和
修改。由于时间、水平等诸多原因,书中必定有不少错误和值得改进的地
方,希望读者多提宝贵意见。我会在最快的时间内把最终更新版本发布出
来。
读者有什么意见和疑问可直接给我发 Email。我会尽力为大家解答的。
谢谢!
现将我的 Email 公布如下:
Email:
WengYB@126.com
第 页
1
第一部分 必备的数学知识
在这最开始的一部分中我们将介绍本书所要用到的数学知识。我们讨论的主题是向量,矩阵和
相应的变换,当然还有一些有关面和线的内容。最开始阅读时这部分是可选的。
本教程对这些知识的讨论是很有限的,因此对于不同数学知识背景的读者来说都容易阅读。对
于想了解更多更全的这方面信息的读者,请查看有关线性代数的书籍。当然已经学习过线性代数的
读者也可将它作为有必要的复习内容来阅读。(这里推荐你看看《线性代数与空间解析几何》)
除此之外,我们还将展示D3DX类中相关的数学模型和执行特殊变换的函数。
目标
z 学习向量的几何和代数性质以及它们的3D计算机图形程序
z 学习矩阵以及学会使用它们来变换3D图形
z 学习怎样用代数方法来对面和线建模以及它们的3D图形程序
z 熟悉用于3D数学运算的D3DX库中包含的类和子程序
三维空间中的向量
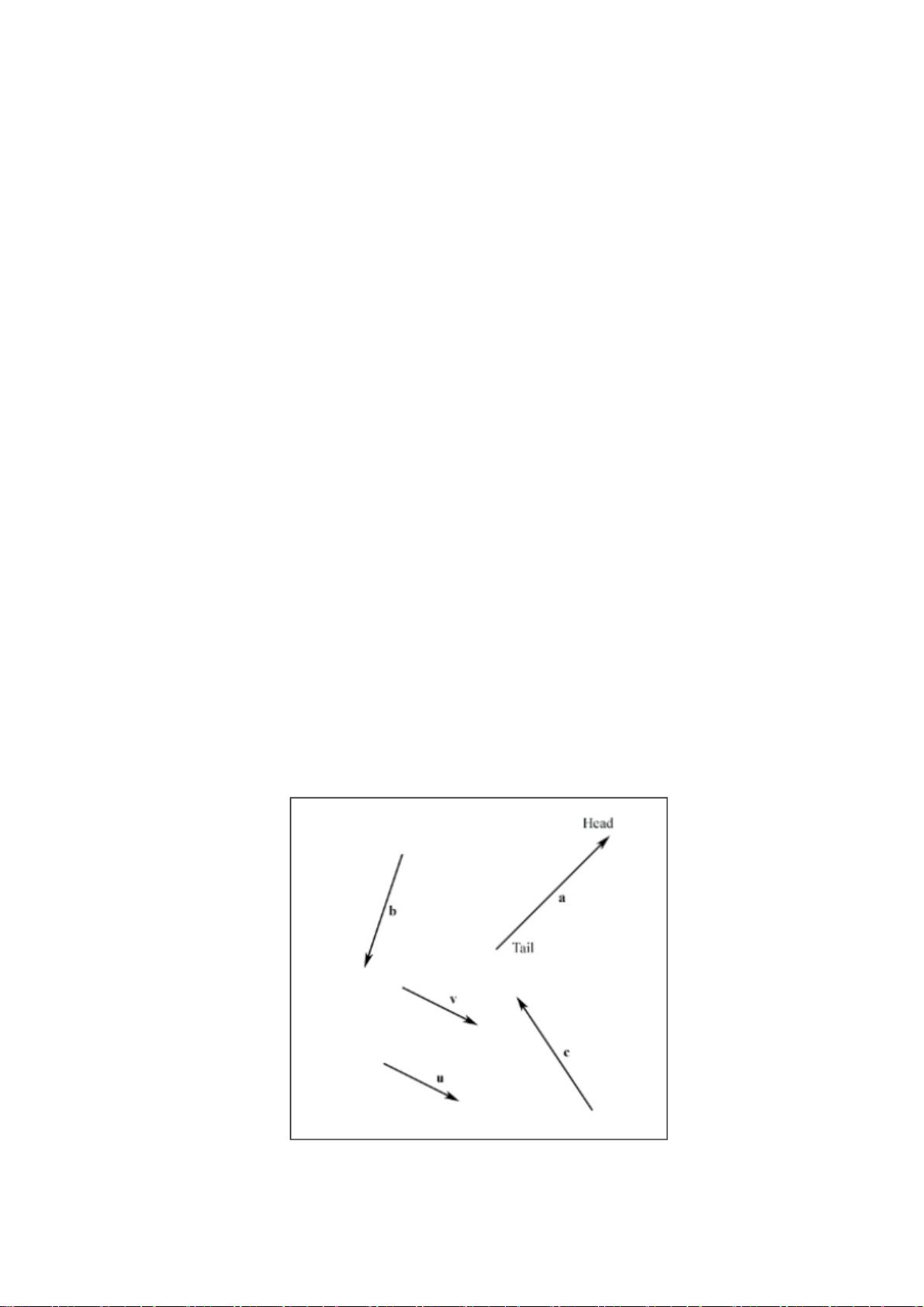
几何学中,我们用有向线段表示向量,如图 1。向量的两个属性是他的长度和他的顶点所指的
方向。因此,可以用向量来模拟既有大小又有方向的物理模型。例如,在第十四章中我们要实现的
粒子系统。我们用向量来模拟粒子的速度和加速度。其他时候,在 3D 计算机图形学中我们仅用向量
来模拟方向。例如我们常常想知道光线的照射方向,多边形的朝向,以及在 3D 世界中摄象机所看的
方向。向量为在 3 维空间中表示方向的提供了方便。
图1
第 页
2
向量与位置无关。有同样长度和方向的两个向量是相等的,即使他们在不同的位置。观察彼此
平行的两个向量,例如在图 1 中 u 和 v 是相等的。
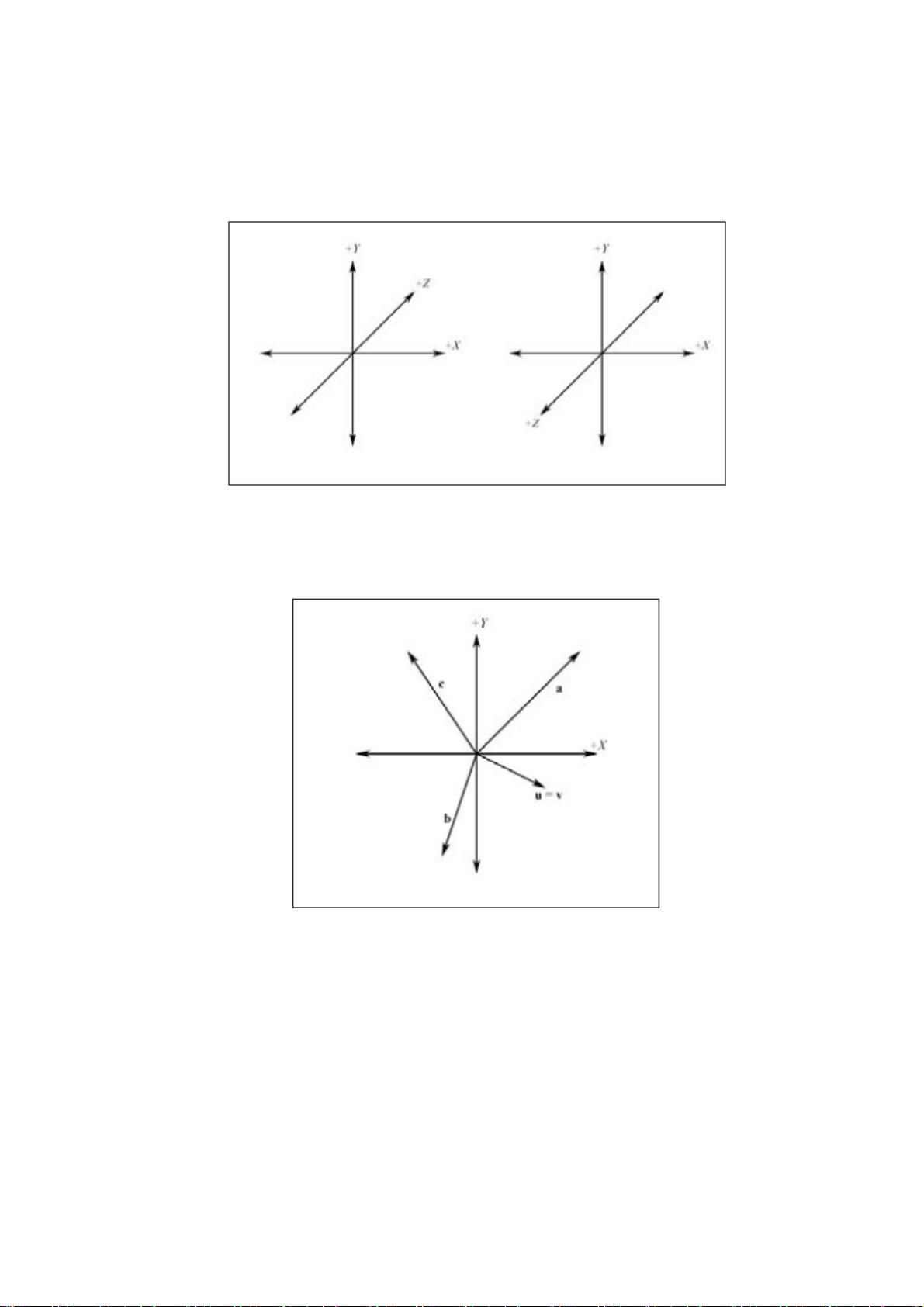
我们继续学习左手坐标系。图 2 显示的是左手坐标系和右手坐标系。两者不同的是 Z 轴的方向。
在左手坐标系中 Z 轴是向书的里面跑的而右手坐标系是向书的外边跑的。
图2
因为向量的位置不能改变它的性质,我们能把所有向量平移使他们的尾部和坐标系的原点重合。
因此,当一个向量在标准位置我们能通过头点来描述向量。图3显示的是图1中的向量在标准位置的
样子。
图3
我们通常用小写字母表示一个向量,但有时也用大写字母。如 2、3 和 4 维向量分别是:u = (
ux
,
uy
), N = (
Nx
,
Ny
,
Nz
), c = (
cx
,
cy
,
cz
,
cw
)。我们现在介绍 3D 中的 4 个特殊向量,就象图 4
显示的。首先是分量都是 0 的向量称为零向量;它被表示成加粗的 0 = (0, 0, 0)。接下来 3 个特
殊的向量是标准向量。分别将其叫做 i, j 和 k 向量,它们分别沿着坐标系的 x 轴,y 轴和 z 轴,并
且只有 1 个单位长:i = (1, 0, 0), j = (0, 1, 0), and k = (0, 0, 1)。
注意:只有1个单位长的向量叫做单位向量。
第 页
3
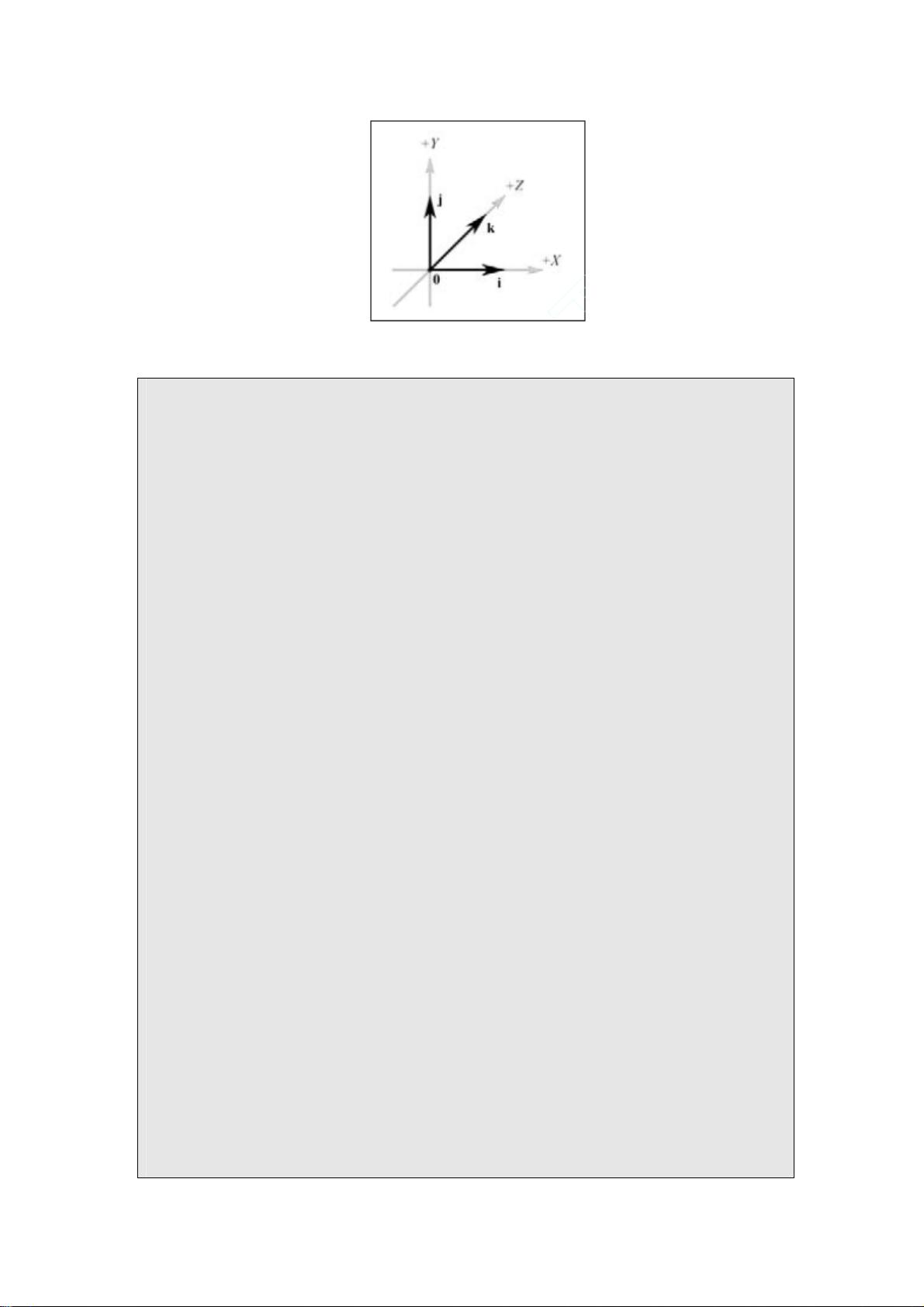
图4
在D3DX库中,我们能用D3DXVECTOR3类表示3维空间中的向量。它的定义是:
typedef struct D3DXVECTOR3 : public D3DVECTOR
{
public:
D3DXVECTOR3() {};
D3DXVECTOR3( CONST FLOAT * );
D3DXVECTOR3( CONST D3DVECTOR& );
D3DXVECTOR3( CONST D3DXFLOAT16 * );
D3DXVECTOR3( FLOAT x, FLOAT y, FLOAT z );
// casting
operator FLOAT* ();
operator CONST FLOAT* () const;
// assignment operators
D3DXVECTOR3& operator += ( CONST D3DXVECTOR3& );
D3DXVECTOR3& operator -= ( CONST D3DXVECTOR3& );
D3DXVECTOR3& operator *= ( FLOAT );
D3DXVECTOR3& operator /= ( FLOAT );
// unary operators
D3DXVECTOR3 operator + () const;
D3DXVECTOR3 operator - () const;
// binary operators
D3DXVECTOR3 operator + ( CONST D3DXVECTOR3& ) const;
D3DXVECTOR3 operator - ( CONST D3DXVECTOR3& ) const;
D3DXVECTOR3 operator * ( FLOAT ) const;
D3DXVECTOR3 operator / ( FLOAT ) const;
friend D3DXVECTOR3 operator * ( FLOAT, CONST struct D3DXVECTOR3& );
BOOL operator == ( CONST D3DXVECTOR3& ) const;
BOOL operator != ( CONST D3DXVECTOR3& ) const;
第 页
4
















评论0