SPM.zip_accept3zb_matlab_synthetic资源-CSDN文库

共2个文件

pdf：1个

m：1个

版权申诉

6 浏览量 2022-07-15 21:16:17 上传评论收藏 131KB ZIP 举报

标题 "SPM.zip_accept3zb_matlab_synthetic" 指涉的是一个使用 MATLAB 编程语言创建的合成自发电位（Synthetic Spontaneous Potential, SPM）数据集或程序包。SPM通常在地质勘探领域中使用，特别是在地球物理的测量中，用于分析地下的自然电位差异。这个特定的压缩包可能包含了用于生成这些数据的MATLAB代码、算法或者仿真结果。描述中的 "synthetic spontaneous potential" 提示我们这个压缩包的内容是人工构建的SPM信号，这可能是为了教学、研究或测试目的。通过模拟真实世界的数据，用户可以理解和学习如何分析SPM数据，以及如何设计或评估相应的处理方法。标签 "accept3zb" 可能是这个项目或算法的一个特定版本或者子模块的名称，但没有足够的上下文来详细解释它的具体含义。它可能代表一种特定的滤波技术、数据处理步骤或者是一个特定的函数库。至于文件列表仅显示了 "SPM"，这可能是压缩包内的主文件或者文件夹名称。通常，MATLAB程序可能包含.m文件（MATLAB脚本或函数）、.mat文件（保存变量的数据文件）或其他相关资源文件。这些文件可能包含了生成SPM信号的代码，数据输入/输出逻辑，或者结果的可视化工具。在MATLAB中，处理SPM数据可能涉及以下知识点： 1. **数据读取与写入**：MATLAB提供了多种函数如`load`和`save`来读取和保存数据，这在处理SPM数据时非常关键，因为原始数据可能来自各种外部设备或文件格式。 2. **信号处理**：MATLAB拥有强大的信号处理工具箱，可以进行滤波、降噪、谱分析等操作，这对于分析SPM信号的特征至关重要。 3. **数值计算**：SPM数据的分析可能涉及复杂的数学运算，例如矩阵运算、微积分、统计分析等，MATLAB提供了丰富的内置函数支持这些运算。 4. **可视化**：MATLAB的`plot`系列函数可以用于绘制SPM信号的时间序列图、频谱图等，帮助理解数据的特性。 5. **自定义函数和类**：用户可能编写了自己的函数或类来封装特定的SPM处理逻辑，这有助于代码重用和模块化。 6. **数据模拟**：合成SPM数据的生成通常涉及到随机数生成、模型参数设定等，以模拟实际地质环境下的电位变化。 7. **优化和拟合**：在处理SPM数据时，可能需要找到最佳拟合模型或者进行参数估计，MATLAB的优化工具箱可以派上用场。 8. **并行计算**：对于大数据量的SPM处理，MATLAB的并行计算工具箱可以帮助加速计算过程。 9. **交互式界面**：如果这个项目包括用户界面，可能使用了MATLAB的App Designer来创建图形用户界面，方便非编程人员操作。 10. **文件I/O接口**：如果SPM数据与其他软件或系统交换，可能涉及到特定的文件格式转换或接口编程。由于具体的代码和数据未给出，以上分析基于一般的MATLAB编程和SPM数据处理背景。要详细了解"accept3zb"的具体含义以及压缩包内文件的详细功能，需要查看实际的源代码和文档。

资源详情

资源评论

资源推荐

收起资源包目录

SPM.zip （2个子文件）

SPM

1-s2.0-S0098300401000358-main.pdf 145KB

SPM.m 96B

Computers & Geosciences 27 (2001) 1127–1133

INVER2DBASE}A program to compute basement depths

of density interfaces above which the density contrast varies

with depth

V. Chakravarthi*, S.B. Singh, G. Ashok Babu

National Geophysical Research Institute, Uppal Road, Hyderabad-500 007, India

Received 1 August 2000; received in revised form 22 January 2001; accepted 23 January 2001

Abstract

A computer program to invert the gravity anomalies of density interfaces above which the density contrast varies

with depth, is presented. The sediment–basement interface is approximated by an N-sided polygon. A function

subprogram GR2DPOL and two subroutine subprograms ZOR2DPOL and SIMEQ support the main program.

Subroutine ZOR2DPOL calculates the initial depth estimates of a density interface at all anomaly points on the

principal proﬁle using the inﬁnite slab approximation. Function subprogram GR2DPOL computes the theoretical

gravity anomaly of a density interface at each anomaly point on the proﬁle and returns to the main program.

Subroutine SIMEQ is used to solve n incremental depth parts of the vertices of a density interface. Partial derivatives

are calculated by a simple ﬁnite-diﬀerence method. Normal equations are constructed and solved by Marquardt’s

algorithm. The proposed inversion scheme is independent on the equal station spacing criteria. The validity of the

algorithm is demonstrated by calculating the basement depths of the Tucson basin, southern Arizona. # 2001 Elsevier

Keywords: Sediment–basement interface; N-sided polygon; Variable density contrast; Gravity anomaly; Inversion

1. Introduction

The computation of basement depths of sedimentary

basins from the observed gravity anomalies is a classic

exercise in regional and hydrocarbon explorations.

While explaining the ambiguity in gravity interpretation

as described by Roy (1962), Rama Rao and Murthy

(1978) opined that the ambiguity could be overcome by

assigning a mathematical geometry to the anomaly

causing body with a known density contrast. The widely

used mathematical geometries in sedimentary basin

modeling are the stacked prism model of Bott (1960)

and the polygonal model of Talwani et al. (1959). In

Bott’s (1960) method of gravity interpretation, the cross-

section of a sedimentary basin above the density

interface was viewed as a series of outcropping

juxtaposed prisms having equal widths, whereas in the

polygonal method of Talwani et al. (1959) the outline of

the basin was approximated by an N-sided polygon.

Most of the existing algorithms that employ either of

these two geometries, assume that the density of

sedimentary rocks above the basement interface is

uniform, and therefore, a constant density is generally

adopted in the modeling schemes (Morgan and Grant,

1963; Bhattacharya and Navolio, 1975). However, ﬁeld

studies show that the density of sedimentary rocks

increases progressively with depth (Hedberg, 1936;

Nettleton, 1934; Maxant, 1980), thereby generat-

ing diﬀerential density values at diﬀerent depths

of deposition. Cordell (1973) opined that the eﬀects of

Code available from server at http://www.iamg.org/

CGEditor/index.htm

*Corresponding author.

E-mail address: postmast@csngri.ren.nic.in (V. Chakra-

varthi).

PII: S 0098-3004(01)00035-8

compaction, stratigraphic layering, facies change, ce-

mentation, diagenesis, tectonic history are responsible

for the variation in density of sedimentary rocks with

depth. Sometimes, it is possible to explain this variation

of density with depth by simple mathematical density

functions and hence, reliable results can be obtained by

considering a variable density in the interpretational

procedures. Cordell (1973), Granser (1987), Chai and

Hinze (1988) simulated the decrease in density contrast

of sedimentary rocks with depth by an exponential

density-depth function. However, no closed form

theoretical gravity expressions can be developed in the

space domain with an exponential density function.

Bhaskara Rao (1986) made use of a quadratic density

function to ascribe the density variation of sedimentary

rocks with depth. Ruotoistenmaki (1992), Garcia-

Abdeslem (1992) also utilized the concept of variable

density in their interpretational techniques. While

explaining the drawbacks of the quadratic density

function, Chakravarthi and Rao (1993) introduced a

parabolic density function to explain the decrease in

density contrast of sedimentary rocks with depth and

successfully adopted the density function in their

modeling scheme to interpret the gravity anomalies of

sedimentary basins. Chakravarthi (1994) made use of

this density function to interpret the gravity anomalies

of non-outcropping sedimentary basins. Later, Viswes-

wara Rao et al. (1994) adopted the density function to

derive a theoretical gravity expression of a two-dimen-

sional arbitrary-shaped body by approximating the

outline of the body as an N-sided polygon. Such an

expression can be used to compute the theoretical

gravity anomalies of sedimentary basins with parabolic

density contrast (PDC ) by specifying the co-ordinates of

the polygon as a part of input (forward modeling).

However, the practical utility of this forward model-

ing scheme is limited in the sense that the depth

ordinates of the ﬂoor of a sedimentary basin are not

known a priori to compute the theoretical gravity

anomalies. In practice, one has to solve the inverse

problem i.e., to ﬁnd out the depth values of the ﬂoor of a

sedimentary basin from the observed gravity anomalies.

In the present paper, we present an inversion scheme

INVER2DBASE to compute the basement depths of

density interfaces above which the density contrast is

assumed to vary with depth. We have adopted the

Marquardt’s (1963) algorithm in the inversion scheme.

2. Forward modeling of a two-dimensional arbitrary

shaped body with PDC

2.1. Parabolic density function

Chakravarthi and Rao (1993) initially introduced the

parabolic density function and later on, simpliﬁed to the

form (Visweswara Rao et al., 1994),

DrðzÞ¼

ðDr

 azÞ

; ð1Þ

where DrðzÞ is the density contrast of a section of a

sedimentary column at any depth z, Dr

is the density

contrast observed at the ground surface i.e., at z ¼ 0 and

a is a constant.

The analytical gravity expression Dgð0Þ at any point

pð0Þ on the principal proﬁle of a two-dimensional

arbitrary shaped body with PDC is given by (Viswes-

wara Rao et al., 1994),

Dgð0Þ¼

k¼1

dgðkÞ; ð2Þ

where dgðkÞ is the gravity contribution of the kth side of

the polygon given by,

dgðkÞ¼2G

kþ1

as2





as1

BðT2  T1Þ

2Aa



C sin i

S2r

S1r

kþ1



: ð3Þ

Here

S1 ¼ Dr

 az

;

S2 ¼ Dr

 az

kþ1

;

R ¼ððx

kþ1

 x

ðz

kþ1

 z

1=2

;

sin i ¼ðz

kþ1

 z

Þ=R;

cos i ¼ðx

kþ1

 x

Þ=R;

C ¼ x

sin i  z

cos i;

A ¼ C

þ 2Dr

aC cos i þ Dr

;

B ¼2Ca cos i  2Dr

;

T1 ¼ arctanððz

þ C cos iÞ=C sin iÞ;

T2 ¼ arctanððz

kþ1

þ C cos iÞ=C sin iÞ

and

¼ðx

þ z

1=2

;

kþ1

¼ðx

kþ1

þ z

kþ1

1=2

;

¼ P=2  f

;

kþ1

¼ P=2  f

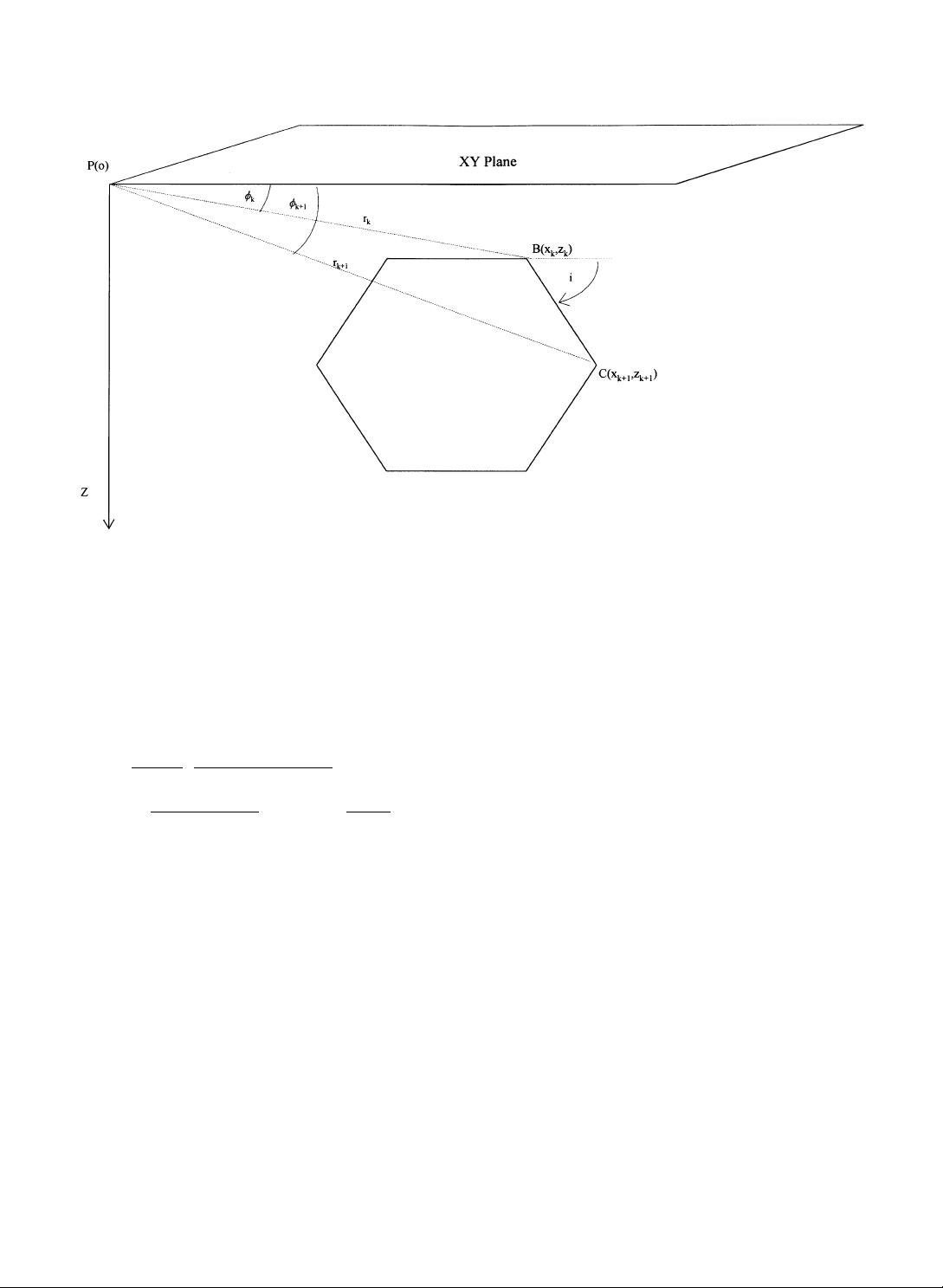
kþ1

are explained in Fig. 1. G

is the Universal Gravitational

Constant.

Here f

, f

kþ1

are the angles made at the point of

calculation by the radial vector r

and r

kþ1

, of the

vertices of the kth side of the polygon with the principal

proﬁle. It can be noted that by putting a ¼ 0 in Eq. (1),

V. Chakravarthi et al. / Computers & Geosciences 27 (2001) 1127–11331128

DrðzÞ becomes Dr

, and from Eqs. (2) and (3) the

gravity eﬀect of a two-dimensional polygon with

uniform density can be calculated, in principle. How-

ever, by putting a¼ 0 in Eq. (3), the ﬁrst three terms of

the equation involve a division by zero. To avoid such

singularities, Eq. (3) can be expressed in a much more

compact form,

dgðkÞ¼

kþ1

ðz

Kþ1

F1 þ CF2Þ





ðz

F1 þ CF2Þ

þ C sin i ln

S1r

kþ1

S2r



; ð4Þ

where

F1 ¼ Dr

þ aC cos i;

F2 ¼ Dr

cos i þ aC

and other terms are explained under Eq. (3). Here the

point of calculation coincides with the origin of the

Cartesian coordinate system. In general, the gravity

contribution dg

ðkÞ of the kth side of the polygon at any

point x

on the principal proﬁle can be calculated by

substituting x

 x

and x

kþ1

 x

for x

and x

kþ1;

respectively, in Eq. (4). Eq. (2) then becomes,

Dgðx

Þ¼

k¼1

ðkÞ: ð5Þ

Therefore, the theoretical gravity anomalies of a

sedimentary basin can be calculated using Eqs. (4) and

(5) by specifying the co-ordinates of the vertices of the

polygon as a part of input (Forward modeling).

3. Inversion of gravity anomalies of density interfaces

While ﬁtting a density interface to a polygonal cross-

section (Fig. 2B), inversion of gravity anomalies amount

to solve for the co-ordinates of the vertices of the

polygon by ﬁtting the anomaly expression, under

consideration, to the observed gravity anomalies by a

least square approach. A detailed account of the

principles of inversion was given by Al-Chalabi (1970,

1972). The inversion process is to solve 2N parametric

values (x

¼ 1toN and z

¼ 1toN of the vertices of the

polygon) from N observations for which many solutions

exists, as the number of unknown parameters exceeds the

number of observations. However, in the present

context, the entire exercise boils down to solve N depth

ordinate values of the polygon from N observations,

uniquely, as the distances to the anomaly points manifest

the x co-ordinates (x

,k¼ 1toN) of the polygon.

4. Method of interpretation

Before attempting the interpretation of a gravity

anomaly proﬁle over a sedimentary basin, the value of

and a of the parabolic density function can be solved

by ﬁtting Eq. (1) to the known density contrast-depth

Fig. 1. Two-dimensional polygonal cross-section.

V. Chakravarthi et al. / Computers & Geosciences 27 (2001) 1127–1133 1129

评论收藏

内容反馈

版权申诉

JaniceLu

粉丝: 95
资源: 1万+

SPM.zip_accept3zb_matlab_synthetic

评论0

最新资源

SPM.zip_accept3zb_matlab_synthetic

评论0

matlab spm

spm.zip_spm_spm power_变频_变频器_变频器 matlab

aal2_for_SPM12.tar.gz_aal2_for_SPM12.tar_fMRI matlab_fmri_spm12

spm.zip_SPM扰动_small perturbation_spm

spm.rar_MATLAB SPM_matlab_薛定谔_spm_薛定谔_薛定谔方程

spm.zip_频率控制

jmc8.0.0-win32.win32.x86_64.zip

SPM.rar_MATLABspm软件_SPM matlab 打包_matlab中spm代码_spm_spm是什么matlab

SPM.rar_SPM PET_fmri_fmri spm_pet_spm

SPM-SRS.rar_BUPTSSE-SPM-LLD_BUPTSSE-SPM-LLD.pdf_SPM-SRS_spm课程网站_

SPM.rar_project management_spm

SPM5.rar_SPM 结构_spm_spm matlab_spm5

SPM.rar_laser_mode locked_mode-locked_spm_激光

二维数据或者图片堆叠形成三维空间的表示.zip_matlab_matlab 图像处理_matlab在一个坐标系画不同三维图_ma

spm.rar_phase noise_spm 啁啾_啁啾非线性_脉冲 相移_非线性SPM

SPM12 初学者指南. SPM12 starter's guide.zip_spm12 中文_spm12 中文教程_spm12

SPM.rar_open_smart spm_spm c＋＋_无网格法_物质点

Spectral_li-ion_SPM-1.3.zip_ION_spm 锂电池_电池spm模型_锂电池_锂电池模型

RISC.zip_ALU SUB_Risc spm_alu risc_alu数据_sub

SPM.rar_SPWM 三相_spwm_三相SPWM_载波调制SPWM

NIRS_SPM.rar_NIRS-SPM_hemoglobin_广义_广义线性_欧拉 定位

NIfTI_20140122.zip_MATLAB nii读取及显示_nii文件_加载nii

spm.rar_DSP正弦_am577_dsp_sinusoidal pwm_vesselsazj

SPM.rar_HH极化_VV极化_后向散射_平面波 极化_粗糙面

dicomserver1419.zip_SPM12 初学者指南_spm12_spm12使用教程

taibao.zip_matlab 光学_matlab衍射_衍射光学_近场远场_远场

SPM.rar_essentialz2u_pleasuree79_三波段_悬浮物 反演_悬浮物反演-三波段算法

Mathieu_Functions_Toolbox_v.1.0.zip_Mathieu 方程_covere63_马蒂厄_马蒂厄仿

spm8_updates_r6313.zip_A9BY_image processing

ImageMagick-6.9.10.68-3.el7.x86_64.rpm

最新资源

spm.rar_phase noise_spm 啁啾_啁啾非线性_脉冲相移_非线性SPM

NIRS_SPM.rar_NIRS-SPM_hemoglobin_广义_广义线性_欧拉定位

SPM.rar_HH极化_VV极化_后向散射_平面波极化_粗糙面

SPM.rar_essentialz2u_pleasuree79_三波段_悬浮物反演_悬浮物反演-三波段算法