-1-
第一章 线性规划
§1 线性规划
在人们的生产实践中,经常会遇到如何利用现有资源来安排生产,以取得最大经济
效益的问题。此类问题构成了运筹学的一个重要分支—数学规划,而线性规划(Linear
Programming 简记 LP)则是数学规划的一个重要分支。自从 1947 年 G. B. Dantzig 提出
求解线性规划的单纯形方法以来,线性规划在理论上趋向成熟,在实用中日益广泛与深
入。特别是在计算机能处理成千上万个约束条件和决策变量的线性规划问题之后,线性
规划的适用领域更为广泛了,已成为现代管理中经常采用的基本方法之一。
1.1 线性规划的实例与定义
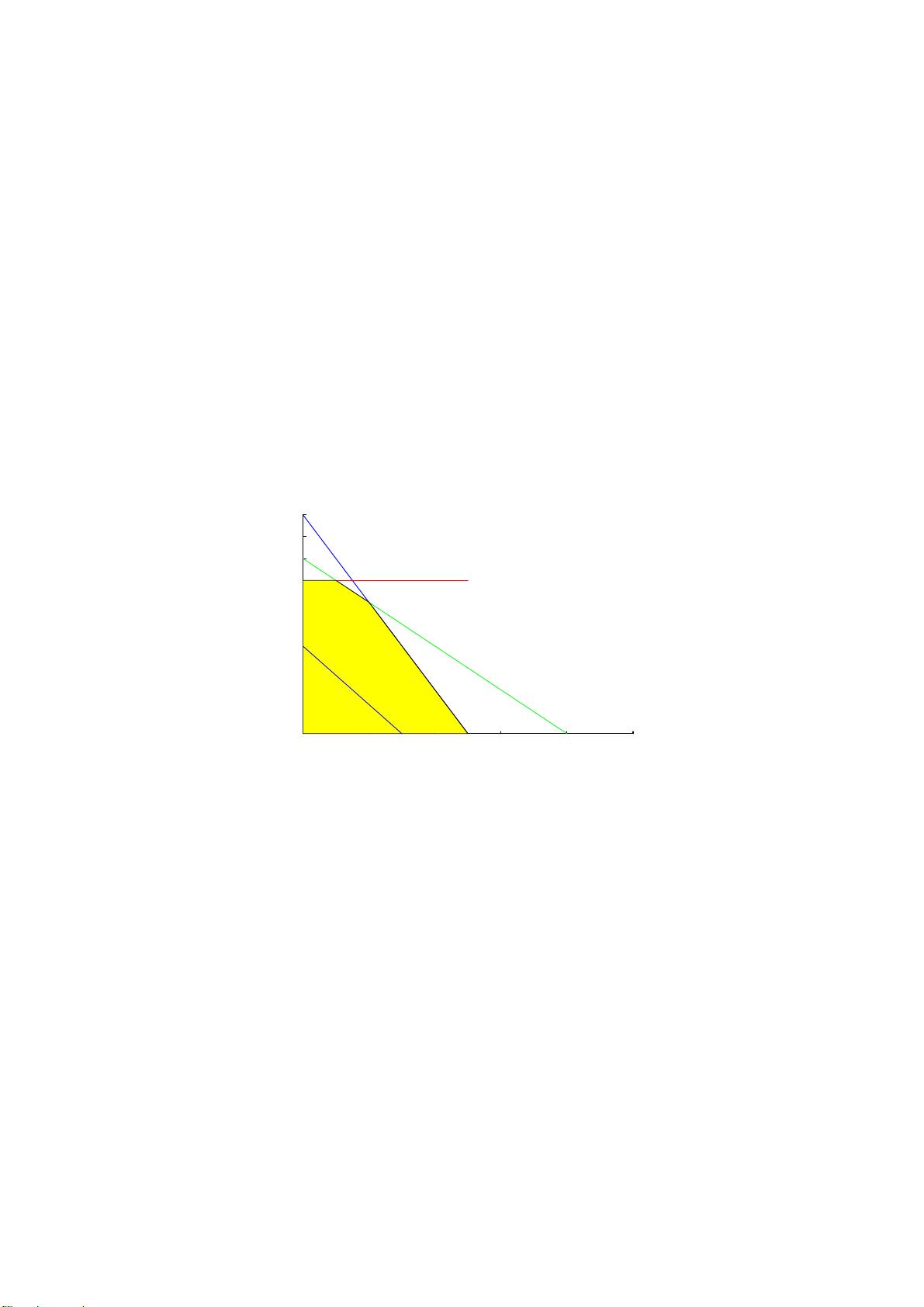
例 1 某机床厂生产甲、乙两种机床,每台销售后的利润分别为 4000 元与 3000 元。
生产甲机床需用
BA、 机器加工,加工时间分别为每台 2 小时和 1 小时;生产乙机床
需用
CBA 、、 三种机器加工,加工时间为每台各一小时。若每天可用于加工的机器时
数分别为
机器 10 小时、
机器 8 小时和 C 机器 7 小时,问该厂应生产甲、乙机床各
几台,才能使总利润最大?
上述问题的数学模型:设该厂生产
1
x 台甲机床和
2
x 乙机床时总利润最大,则
21
, xx
应满足
(目标函数)
21
34max xxz
=
(1)
s.t.(约束条件)
⎪
⎪
⎩
⎪
⎪
⎨
⎧
≥
≤
≤+
≤+
0,
7
8
102
21
2
21
21
xx
x
xx
xx
(2)
这里变量
21
, xx 称之为决策变量,(1)式被称为问题的目标函数,(2)中的几个不等式
是问题的约束条件,记为 s.t.(即 subject to)。由于上面的目标函数及约束条件均为线性
函数,故被称为线性规划问题。
总之,线性规划问题是在一组线性约束条件的限制下,求一线性目标函数最大或最
小的问题。
在解决实际问题时,把问题归结成一个线性规划数学模型是很重要的一步,但往往
也是困难的一步,模型建立得是否恰当,直接影响到求解。而选适当的决策变量,是我
们建立有效模型的关键之一。
1.2 线性规划的 Matlab 标准形式
线性规划的目标函数可以是求最大值,也可以是求最小值,约束条件的不等号可以
是小于号也可以是大于号。为了避免这种形式多样性带来的不便,Matlab 中规定线性
规划的标准形式为
xc
x
T
min
s.t.
⎪
⎩
⎪
⎨
⎧
≤≤
=⋅
≤
ubxlb
beqxAeq
bAx
其中
c 和
为 n 维列向量, A、 Aeq 为适当维数的矩阵, b 、 beq 为适当维数的列向
量。