shortest_path_between_cities.rar_between_最短距离

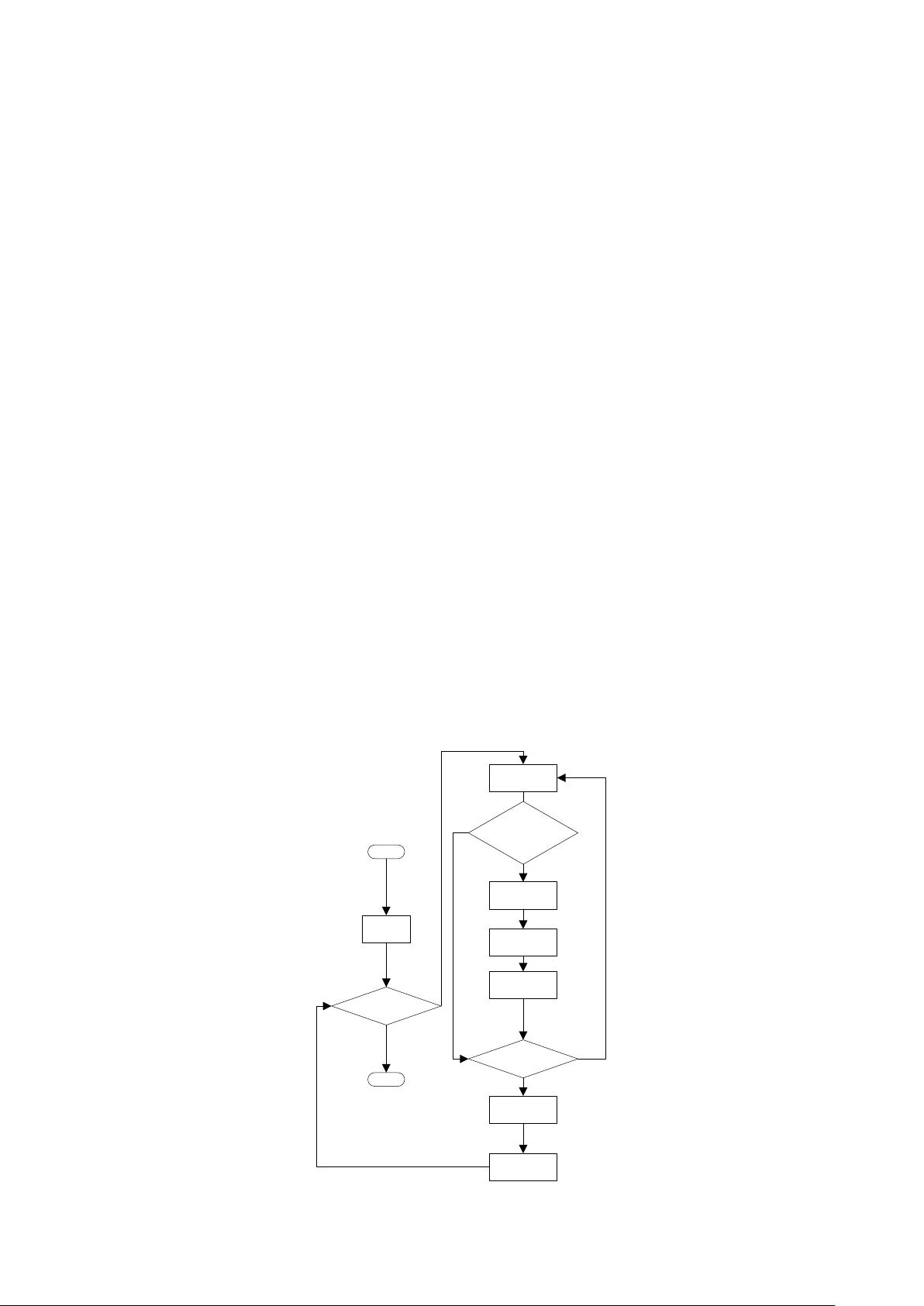
标题中的"shortest_path_between_cities.rar_between_最短距离"表明了我们正在处理一个关于城市间最短路径的问题，而“最短距离”是指在特定的网络或图中寻找两个点之间路径的成本最低的方式。这通常涉及到图论中的算法，如Dijkstra算法或Floyd-Warshall算法。 描述中提到的“在50个城市中，找到城市1与城市50之间的最短距离和最小花费”进一步细化了问题。这暗示我们有一个包含50个节点（代表城市）的图，每个节点之间可能存在边，边可能带有权重（代表距离或费用）。我们的目标是找出从城市1到城市50具有最小总权重的路径。 标签“between 最短距离”再次强调了我们要解决的核心问题。 压缩包内的文件可能包含以下信息： 1. "sp.cpp"：这是一个C++源代码文件，很可能实现了计算最短路径的算法。可能是Dijkstra或者Floyd-Warshall，也可能是一个自定义的解决方案。 2. "单源最短路径程序说明.docx"：这个文档可能是对源代码的解释，包括算法的工作原理、输入输出格式以及如何运行程序。 3. "Assignment_2.pdf"：这可能是一个作业或项目说明，详细描述了问题背景、要求和评估标准。 4. "m1.txt" 和 "m2.txt"：这两个文本文件可能包含了图的边和权重数据，每行可能表示一条边及其对应的权重，或者以其他形式存储图的信息。 5. "www.pudn.com.txt"：这可能是一个链接或者引用的来源，可能提供了更多的背景信息或相关的资源。 要解决这个问题，我们需要理解图的数据结构，例如邻接矩阵或邻接表，然后选择适当的算法来查找最短路径。Dijkstra算法适用于没有负权重边的情况，而Floyd-Warshall则可以处理所有类型的边，但效率相对较低。一旦有了算法实现，我们可以读取数据文件（如m1.txt和m2.txt）中的信息，将其转化为图的数据结构，并运行算法找到最短路径。 在实际应用中，这种问题可能出现在交通规划、物流配送、网络路由优化等场景。计算出最短路径不仅可以节省时间和成本，还有助于做出最优决策。对于学习者来说，理解和实现这样的算法是提升编程技能和解决问题能力的重要步骤。