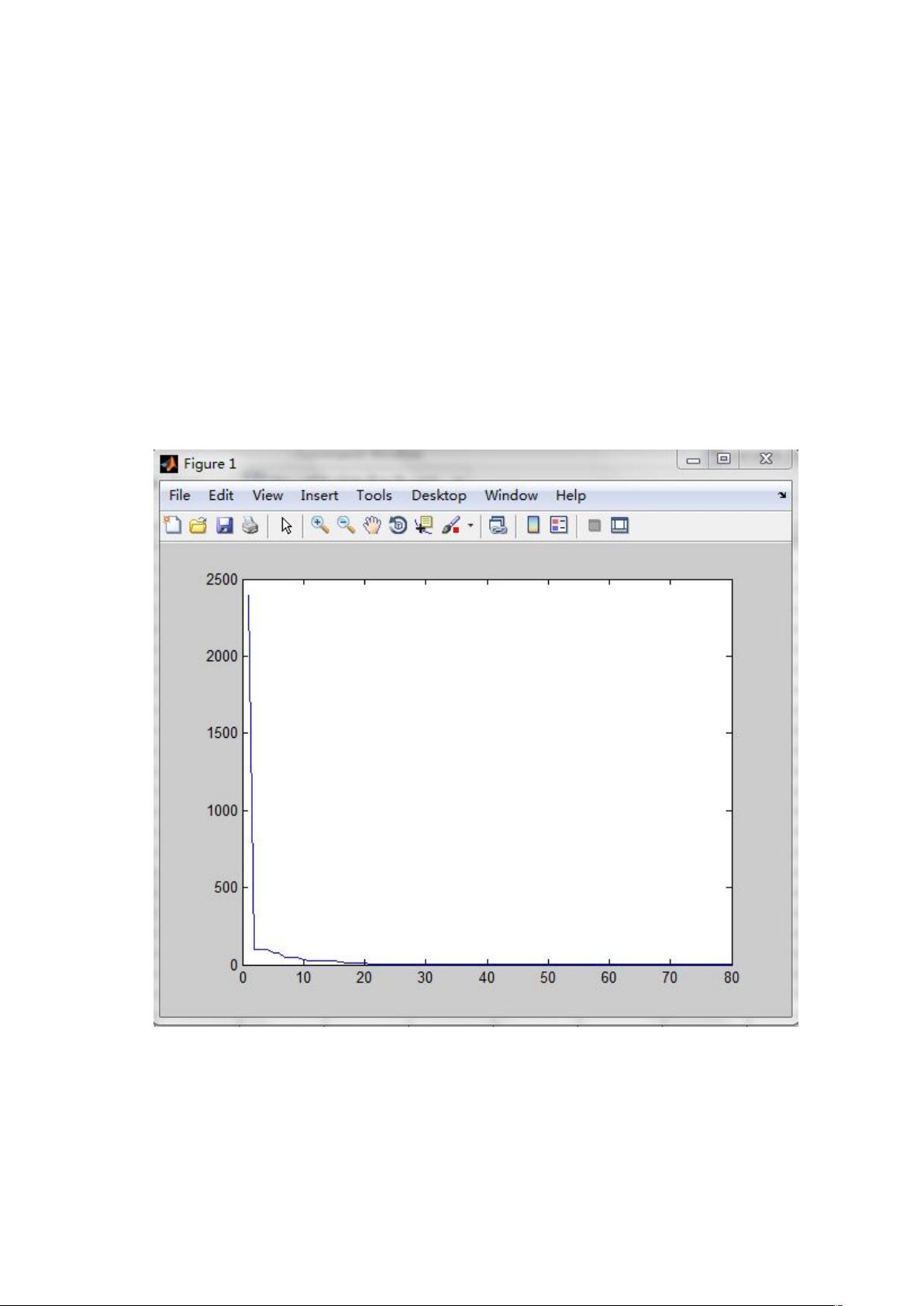
《通用复合形法在Matlab中的应用：最优控制与图形可视化》
在工程和科学研究中，最优控制问题始终是一个重要且具有挑战性的研究领域。这一问题的核心在于如何找到一条使得特定性能指标达到最优的控制输入序列。性能指标可以是成本最低、时间最短、能耗最少等，视具体应用场景而定。为了解决这类问题，研究者和工程师们开发了各种方法，其中，复合形法因其在处理非线性、多约束问题时的强大能力，成为了一个广受欢迎的工具。
复合形法是一种启发式算法，它利用多边形（复合形）在问题的可行域中进行搜索，通过迭代操作逐渐逼近最优解。这种算法的基本思想是：首先构造一个由多个顶点组成的初始复合形，然后通过比较和迭代过程中的替换，使复合形逐步缩小范围并最终收敛到全局最优解。它的优势在于不需要问题的梯度信息，这使得其适用于更为广泛的非光滑或非连续问题。
在Matlab环境下，复合形法的应用得到了极大的便利。Matlab作为一种强大的数学软件，其矩阵运算能力及丰富的函数库，为算法的实现提供了极好的支持。通过Matlab编程，可以轻松构建复合形，进行迭代计算，以及调用内置的优化工具箱函数，以求解最优控制问题。此外，Matlab还提供了一系列的图形化工具，使得算法的可视化处理成为可能。在进行最优控制问题求解时，Matlab允许开发者通过图形界面展示出寻优过程，如多边形边界的绘制、解的演化路径以及控制变量随时间变化的曲线等，从而提供直观的操作展示和结果分析。
复合形法在Matlab中的应用可以概括为几个步骤。首先是初始化复合形，选择一个初始解集合，构成一个多边形，并根据问题的约束条件对其进行校验和调整。接下来，是算法的迭代过程，包括复合形的移动、变形和收缩。在每次迭代中，算法会比较各个顶点所代表的解的优劣，并据此更新复合形，直到满足收束条件，即解的变化量小于某一预设阈值，或迭代次数达到上限。在这个过程中，Matlab的图形化功能能够将每一步的变化以图形的形式展现出来，为用户提供了观察算法进展的直观方式。
在实际应用中，复合形法在Matlab中的实现可以用于多种场景。例如，在航空航天领域，复合形法可以帮助设计出最优的飞行轨迹，从而减少燃料消耗，提高任务执行的经济性和安全性。在电力系统调度中，它可以寻找到满足各种约束条件下的最优发电计划，以最小化成本或提高能源利用率。此外，复合形法还在工业过程控制、机器人路径规划等领域发挥着重要作用。
总结来说，《通用复合形法程序（Matlab）》为解决最优控制问题提供了一种集成化解决方案。它不仅将Matlab强大的计算和图形化能力结合在一起，而且为用户提供了处理非线性、多约束最优控制问题的有力工具。这种程序的应用能够极大地提高研究和工程实践中的问题解决效率，推动相关领域的技术进步。通过深入学习和掌握这一程序，无论是科研人员还是工程师，都能够更好地理解和应用复合形法，解决复杂问题，创造实际价值。
评论1