fft.rar_fft傅里叶

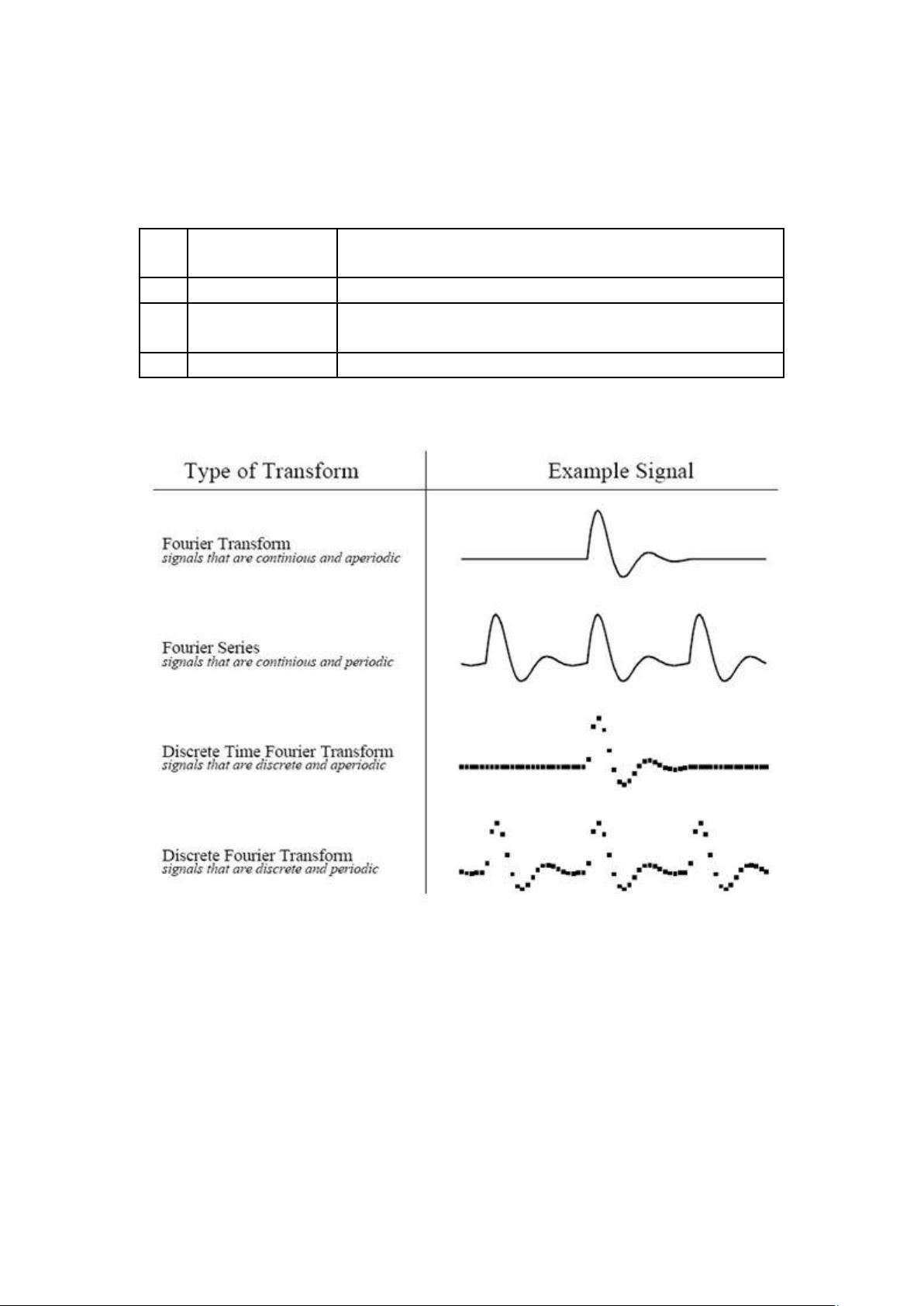
**快速傅里叶变换(FFT)详解** 快速傅里叶变换（Fast Fourier Transform，简称FFT）是计算离散傅里叶变换（Discrete Fourier Transform，DFT）的一种高效算法，由Cooley和Tukey在1965年提出。DFT在信号处理、图像分析、工程计算等领域有着广泛的应用，但其直接计算的复杂度为O(N^2)，对于大尺寸的数据处理效率较低。而FFT通过巧妙的分解和重排方法，将计算复杂度降低到O(N log N)，极大地提高了运算速度。 ### 1. 傅里叶变换基础 傅里叶变换是一种数学工具，能够将一个时域或空间域的信号转换为其频域表示。在数字信号处理中，离散傅里叶变换(DFT)是用于处理离散时间序列的重要工具。DFT计算公式为： \[ X[k] = \sum_{n=0}^{N-1} x[n] e^{-j 2\pi kn/N} \] 其中，\( x[n] \)是输入序列，\( X[k] \)是对应的频率分量，\( N \)是序列长度，\( j \)是虚数单位。 ### 2. FFT算法原理 FFT算法的核心思想是将大问题分解成小问题来解决，利用“分治法”策略。它基于以下两个关键步骤： - **蝶形运算(Dit)**：将DFT分解为两半，分别对这两半进行FFT，然后将结果组合。 - **二分展开(DIF)**：将DFT表达式中的复指数项按二进制展开，使计算更加简洁。 具体过程包括： 1. **分解**：将N点DFT分解为两个N/2点DFT。 2. **重排**：对输入序列进行位反转，即将第n个元素放到第(n反码)个位置。 3. **蝶形运算**：通过一系列乘加运算（蝶形结构）组合小规模的DFT。 4. **递归**：重复以上步骤，直到子问题足够小可以直接求解。 ### 3. Cooley-Tukey算法 Cooley-Tukey算法是最常见的FFT实现方式，分为“下采样”（radix-2）和“不完全分解”（radix-r）两种。其中，radix-2算法假设N是2的幂，适用于大多数情况。它通过两次蝶形运算实现，一次在实部，一次在虚部。 ### 4. 其他FFT变种 除了Cooley-Tukey，还有其他类型的FFT算法，如Bluestein's chirp-z transform、Good-Thomas algorithm、Prime-factor algorithm等，它们适应不同的数据特性或计算环境。 ### 5. FFT的应用 FFT在多个领域有重要应用： - **信号处理**：滤波、频谱分析、谱估计等。 - **图像处理**：频域去噪、图像增强、压缩。 - **通信**：调制解调、信道均衡。 - **数值计算**：微分方程求解、矩阵运算。 - **科学计算**：量子力学、流体力学的模拟。 ### 6. 实现与优化 实际应用中，FFT的实现要考虑效率和精度。例如，使用库函数如FFTW、Intel MKL等可以获取高效的实现。同时，硬件加速如GPU计算、FPGA设计也能进一步提升性能。 总结，FFT是一种高效的离散傅里叶变换算法，它在各种计算任务中扮演着至关重要的角色。理解并掌握FFT的基本原理和应用，对于深入理解和利用这些技术至关重要。