
第
第
2
2
章
章
递
递
归
归
与
与
分
分
治
治
策
策
略
略
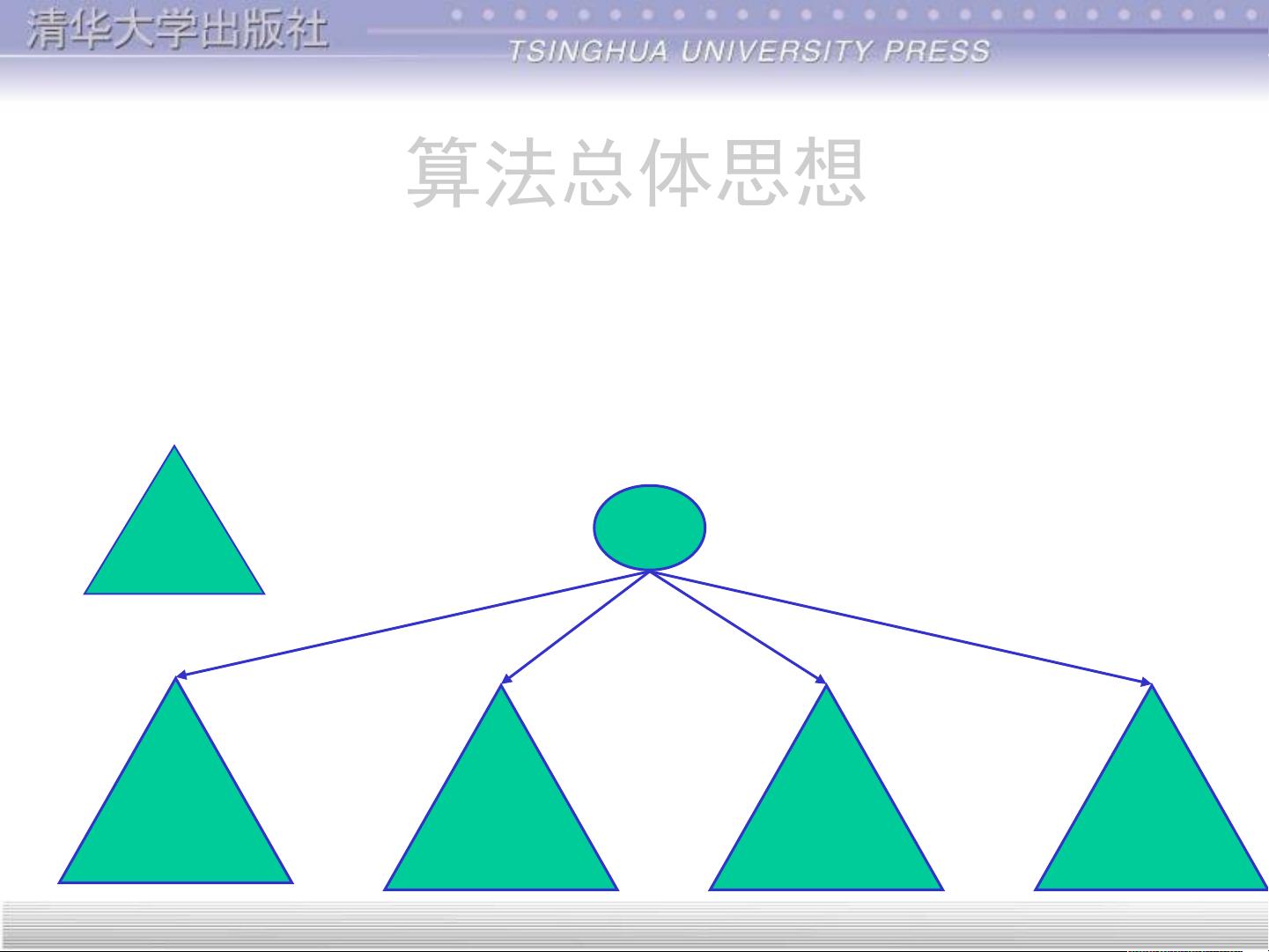
• 将要求解的较大规模的问题分割成k个更小规模的子问
题。
算
算
法
法
总
总
体
体
思
思
想
想
n
T(n/2)
T(n/2) T(n/2) T(n/2)
T(n)
=
• 对这k个子问题分别求解。如果子问题的规模仍然不够
小,则再划分为k个子问题,如此递归的进行下去,直
到问题规模足够小,很容易求出其解为止。
算
算
法
法
总
总
体
体
思
思
想
想
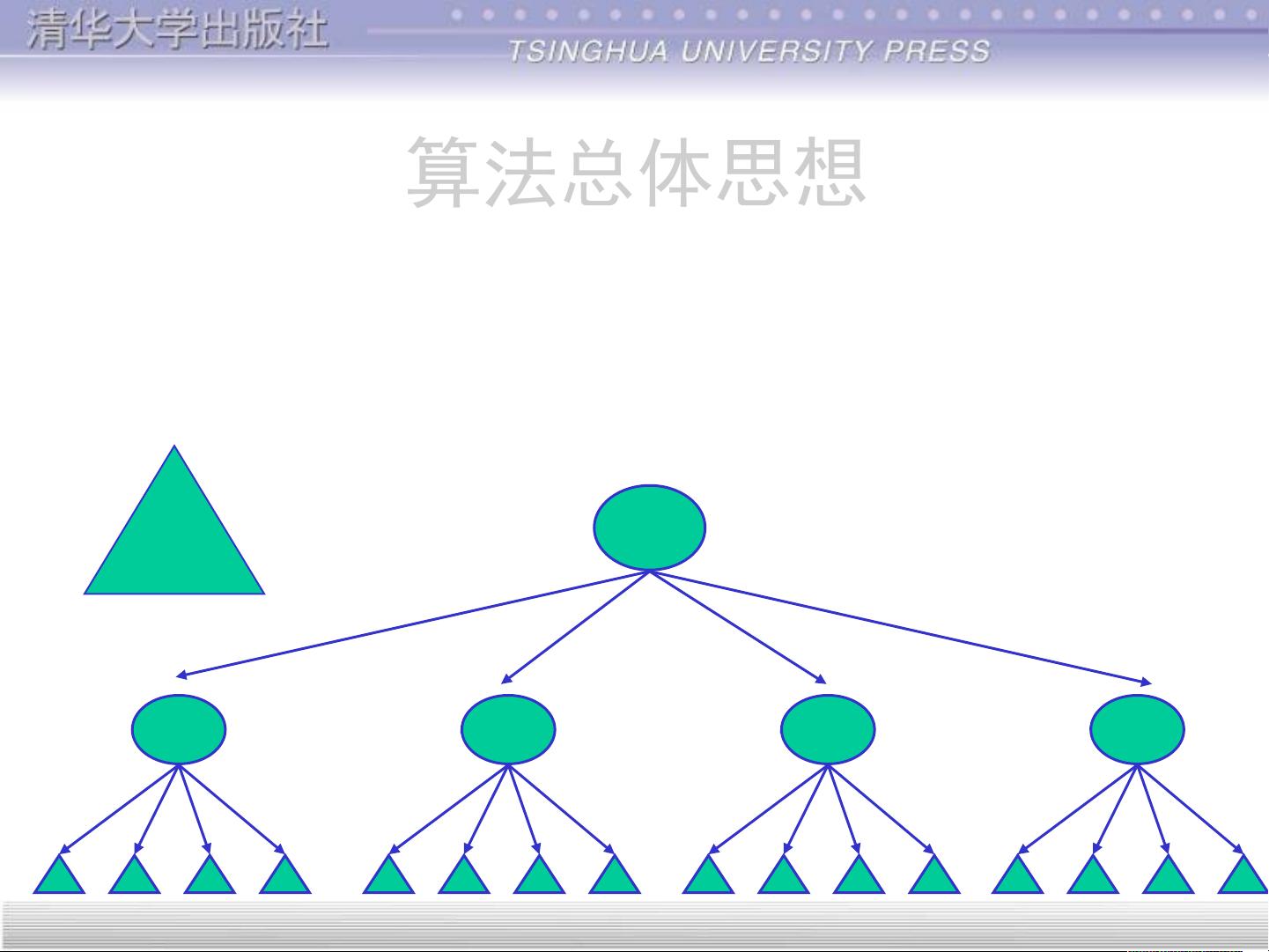
• 对这k个子问题分别求解。如果子问题的规模仍然不够
小,则再划分为k个子问题,如此递归的进行下去,直
到问题规模足够小,很容易求出其解为止。
n
T(n)
=
n/2
T(n/4)T(n/4)T(n/4)T(n/4)
n/2
T(n/4)T(n/4)T(n/4)T(n/4)
n/2
T(n/4)T(n/4)T(n/4)T(n/4)
n/2
T(n/4)T(n/4)T(n/4)T(n/4)
• 将求出的小规模的问题的解合并为一个更大规模的问
题的解,自底向上逐步求出原来问题的解。
算
算
法
法
总
总
体
体
思
思
想
想
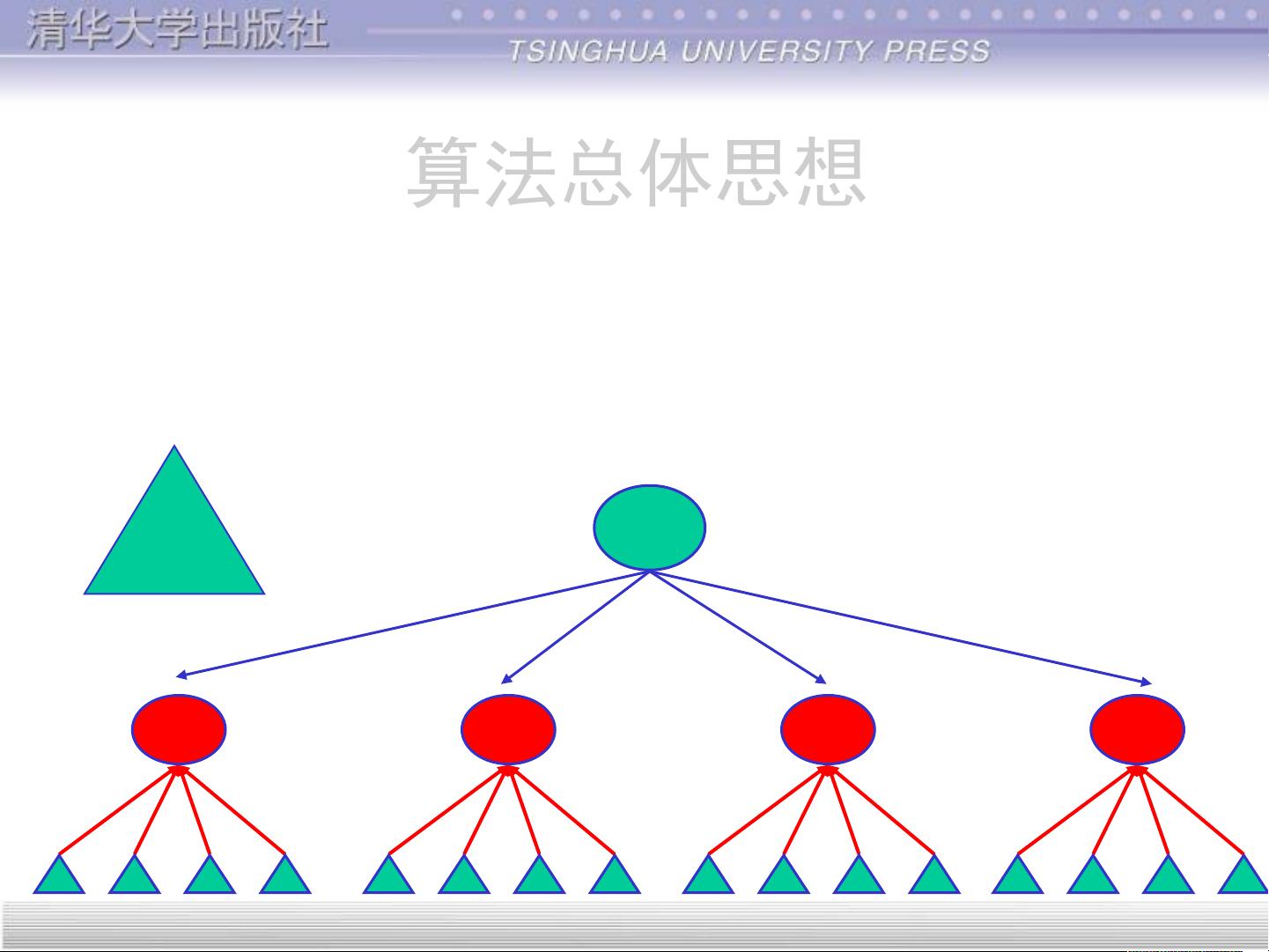
• 将求出的小规模的问题的解合并为一个更大规模的问
题的解,自底向上逐步求出原来问题的解。
n
T(n)
=
n/2
T(n/4)T(n/4)T(n/4)T(n/4)
n/2
T(n/4)T(n/4)T(n/4)T(n/4)
n/2
T(n/4)T(n/4)T(n/4)T(n/4)
n/2
T(n/4)T(n/4)T(n/4)T(n/4)

算
算
法
法
总
总
体
体
思
思
想
想
• 将求出的小规模的问题的解合并为一个更大规模的问
题的解,自底向上逐步求出原来问题的解。
n
T(n)
=
n/2
T(n/4)T(n/4)T(n/4)T(n/4)
n/2
T(n/4)T(n/4)T(n/4)T(n/4)
n/2
T(n/4)T(n/4)T(n/4)T(n/4)
n/2
T(n/4)T(n/4)T(n/4)T(n/4)
分治法的设计思想是,将一个难以直接解决的大问题,
分割成一些规模较小的相同问题,以便各个击破,
分而治之。
凡治众如治寡,分数是也。
----孙子兵法















