三角函数公式Math_Resources_Trigonometric_Formulas.pdf

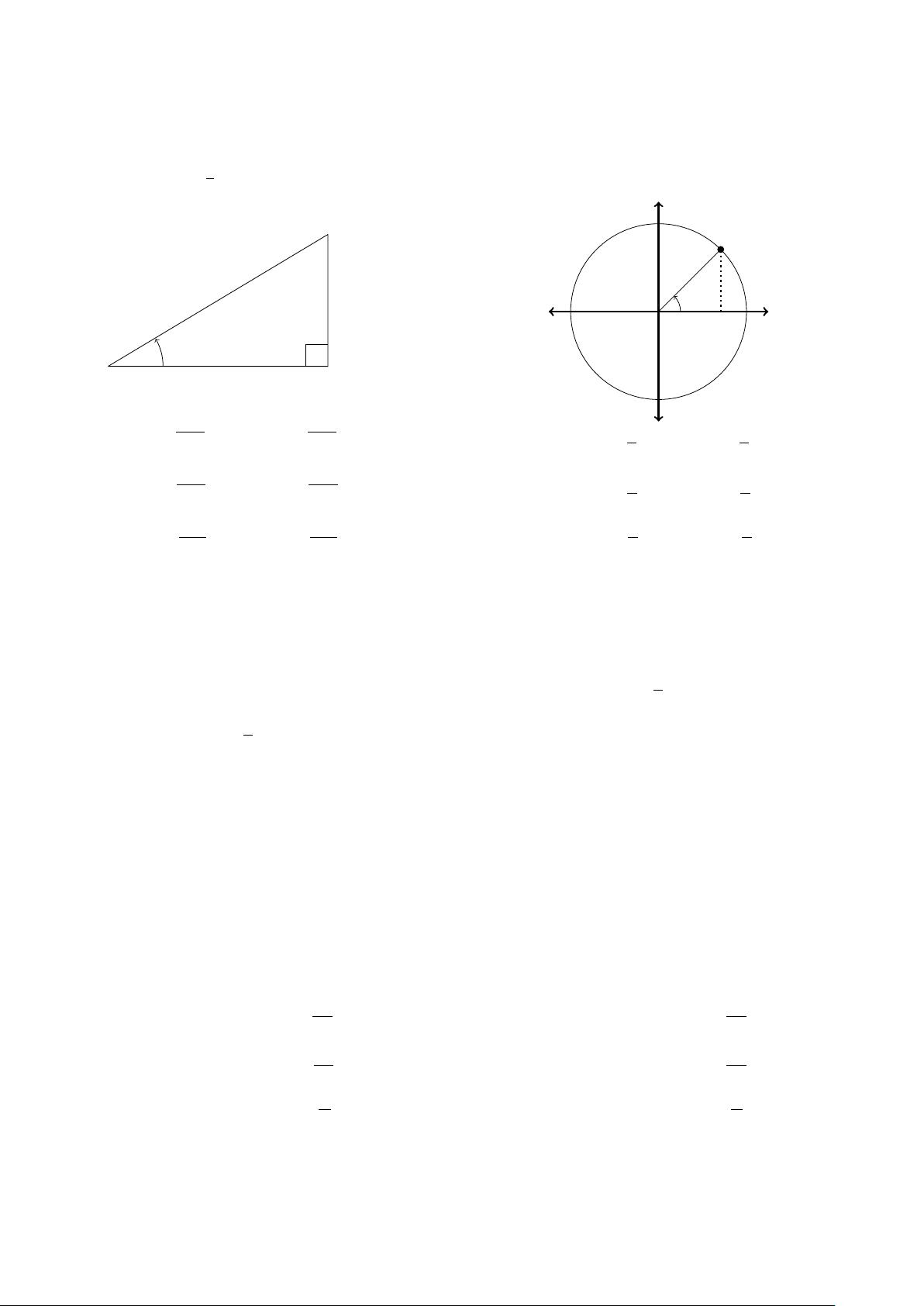
三角函数是数学中的一类重要函数，主要用于解决与角度和距离相关的几何问题，广泛应用于工程、物理学、计算机科学等领域。三角函数公式通常包括正弦、余弦、正切、余切、正割、余割等函数的定义、性质、关系式以及它们的和差、倍角、半角、积化和差、和差化积等变换公式。 根据提供的文件内容，我们可以提炼出以下知识点： 1. 三角函数的基本定义： - 通过直角三角形定义：假设0<θ<π/2或0°<θ<90°，正弦（sinθ）、余弦（cosθ）、正切（tanθ）、余切（cotθ）、正割（secθ）和余割（cscθ）可以通过直角三角形的边长比来定义。 - 通过单位圆定义：定义角度可以是任意值，x和y坐标表示圆上一点，由此定义六个基本三角函数。 2. 三角函数的定义域和值域： - sinθ, cosθ, tanθ, cotθ的定义域是实数集全体(-∞, +∞)，余割（cscθ）和正割（secθ）的定义域是除去使得分母为零的点。 - 各三角函数的值域分别为sinθ和cosθ的值域是[-1, 1]，tanθ和cotθ的值域是(-∞, +∞)，cscθ和secθ的值域是(-∞, -1] ∪ [1, +∞)。 3. 三角函数的周期性： - 周期函数的周期是指函数值重复的最小正数间隔。基本三角函数sinθ, cosθ, tanθ的周期分别是2π，2π和π。 4. 三角函数的恒等式和公式： - 倒数恒等式：sinθ, cosθ, tanθ, cotθ, cscθ和secθ之间存在倒数关系。 - 倍角公式：涉及角度的二倍，如sin(2θ)=2sinθcosθ，cos(2θ)=cos²θ-sin²θ等。 - 半角公式：如tan(θ/2) = √((1-cosθ)/(1+cosθ))等。 - 勾股恒等式：sin²θ + cos²θ = 1，tan²θ + 1 = sec²θ，1 + cot²θ = csc²θ。 - 奇偶公式：如sin(-θ) = -sinθ，cos(-θ) = cosθ等。 - 和差公式：sin(α±β)，cos(α±β)，tan(α±β)等表达式。 - 积化和差与和差化积公式：将三角函数的乘积转化为和或差，或将和或差转化为乘积。 - 双角公式：sin²θ、cos²θ、tan²θ等的表示方式。 - 和差角公式：sinα±sinβ、cosα±cosβ等的表达式。 - 度数与弧度的换算公式：角度与弧度之间的换算关系。 以上内容涵盖了三角函数的多个基本知识点，包括定义、性质、计算方法和应用。掌握这些知识对于解决工程、物理、计算机图形学等相关领域的实际问题至关重要。