第 8 章 图
教材中练习题及参考答案
1. 图G是一个非连通图,共有28条边,则该图至少有多少个顶点?
答:由于G是一个非连通图,在边数固定时,顶点数最少的情况是该图由两个连通分
量构成,且其中之一只含一个顶点(没有边),另一个为完全无向图。设该完全无向图的
顶点数为n,其边数为n(n-1)/2,即 n(n-1)/2=28,得 n=8。所以,这样的非连通图至少有1+8=9
个顶点。
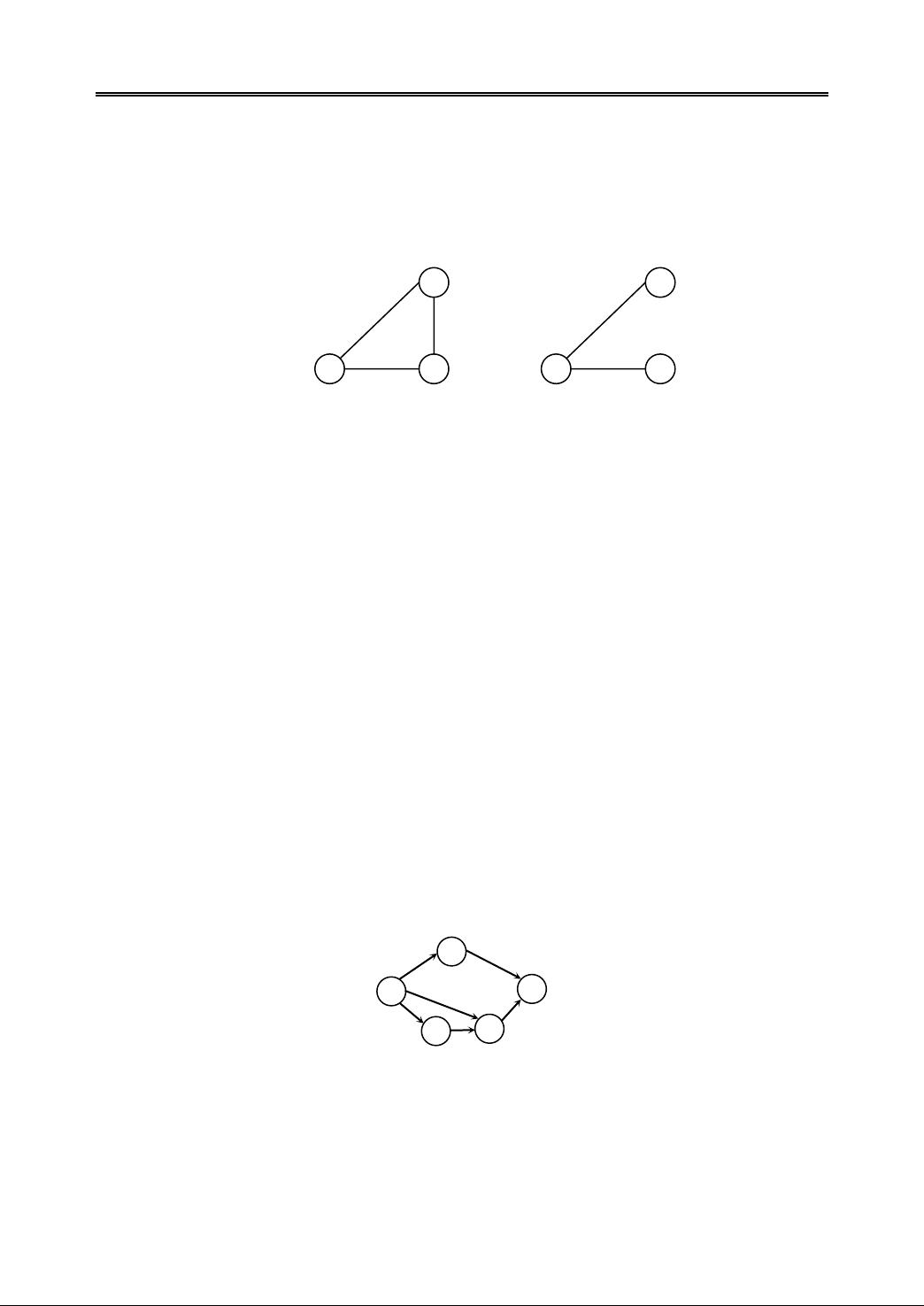
2. 有一个如图 8.2(a)所示的有向图,给出其所有的强连通分量。
答:图中顶点0、1、2构成一个环,这个环一定是某个强连通分量的一部分。再考察顶
点3、4,它们到这个环中的顶点都有双向路径,所以将顶点3、4加入。考察顶点5、6,它
们各自构成一个强连通分量。该有向图的强连通分量有3个,如图8.2(b)所示。
图
8.2
一个有向图及其强连通分量
3. 对于稠密图和稀疏图,采用邻接矩阵和邻接表哪个更好些?
答:邻接矩阵适合于稠密图,因为邻接矩阵占用的存储空间与边数无关。邻接表适合
于稀疏图,因为邻接表占用的存储空间与边数有关。
4. 对 n 个顶点的无向图和有向图(均为不带权图),采用邻接矩阵和邻接表表示时,
如何求解以下问题:
(1)图中有多少条边?
(2)任意两个顶点i和j是否有边相连?
(3)任意一个顶点的度是多少?
答:(1)对于邻接矩阵表示的无向图,图的边数等于邻接矩阵数组中为1的元素个数
除以2;对于邻接表表示的无向图,图中的边数等于边结点的个数除以2。
对于邻接矩阵表示的有向图,图中的边数等于邻接矩阵数组中为1的元素个数;对于邻
0
1
3
2
4
5
6
(a) 一个有向图
(b) 3 个强连通分量
0
1
3
2
4
5
6