精确一维搜索法 对分法 等间隔搜索法

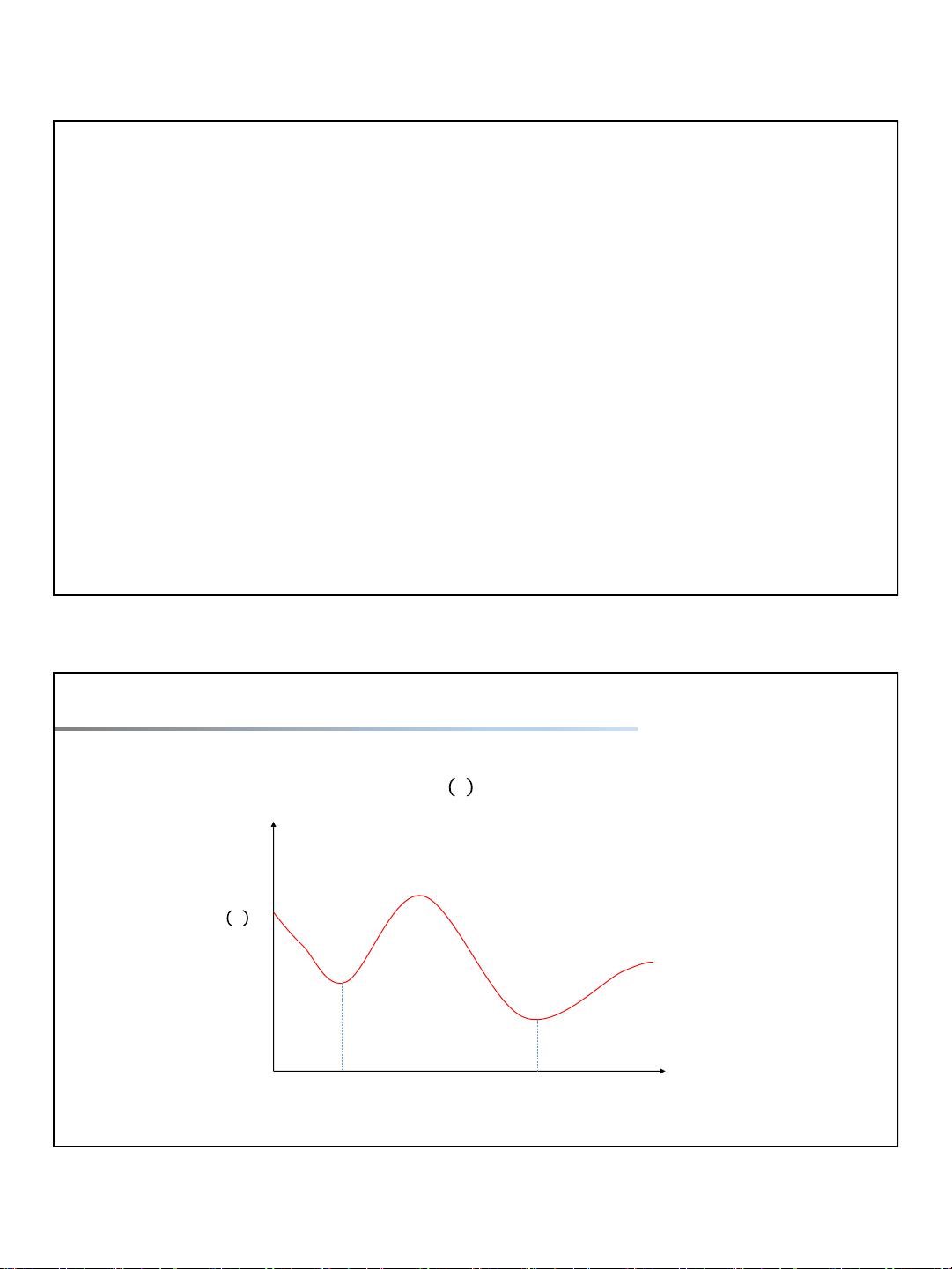
### 精确一维搜索法详解：对分法与等间隔搜索法 #### 一、引言 在数学和计算机科学领域，特别是在最优化理论和技术中，一维搜索法是一种重要的工具，用于找到给定函数的一维最优解。这类方法广泛应用于工程设计、经济模型以及各种科学计算场景中。本篇文章将详细介绍几种常见的精确一维搜索方法，包括对分法（二分法）、等间隔搜索法等，并探讨它们的应用和优缺点。 #### 二、区间消去法（搜索法） 区间消去法是一类通过逐步缩小搜索范围来逼近最优解的方法。这种方法的核心思想是在给定的搜索范围内选取几个测试点，通过比较这些测试点处函数值的大小来判断最优解所在的子区间，从而不断缩小不确定区间的长度直到满足特定的精度要求。下面将分别介绍几种典型的区间消去法： ##### 2.1 对分搜索法 对分搜索法，也称为二分法，是最简单且直观的一种区间消去法。该方法的工作原理是这样的：假设我们有一个单峰函数\(\phi(\alpha) = f(x + \alpha d)\)，其中\(f\)是从\(\mathbb{R}^n\)映射到\(\mathbb{R}\)的函数，\(x\)是初始点，\(d\)是下降方向，而\(\alpha\)是我们希望找到的最优步长。初始不确定区间为\([\alpha_L, \alpha_U]\)。每次迭代时，我们选择不确定区间的中点\(\alpha_M\)，计算\(\phi(\alpha_M)\)。如果\(\phi(\alpha_M)\)小于\(\phi(\alpha_L)\)，则说明最优解位于\([\alpha_M, \alpha_U]\)内；反之，则最优解位于\([\alpha_L, \alpha_M]\)内。通过这种方式不断缩小不确定区间，直到其长度小于预定义的精度\(\epsilon\)。 ##### 2.2 等间隔搜索法 等间隔搜索法也是一种区间消去法，其特点是按照固定间隔在不确定区间内选取测试点。具体来说，假设初始不确定区间为\([\alpha_L, \alpha_U]\)，我们将此区间均匀分为\(N\)个子区间，然后计算每个子区间的端点处函数的值。通过比较这些函数值，可以确定最优解所在的子区间，从而将不确定区间缩小至新的子区间。这个过程重复进行，直到不确定区间的长度满足预定义的精度要求为止。 ##### 2.3 对称区间搜索法 对称区间搜索法主要包括Fibonacci法和黄金分割法。 - **Fibonacci法**：Fibonacci法基于Fibonacci序列来确定测试点的位置。这种方法的关键在于它能够在每次迭代中仅评估一个新点，从而减少函数值的计算次数。具体而言，在第\(k\)次迭代中，不确定区间的长度被分成两个不相等的部分，比例由Fibonacci数列中的相邻两项决定。 - **黄金分割法**：黄金分割法与Fibonacci法类似，但使用了黄金比例\((1 + \sqrt{5})/2\)来划分不确定区间。这种方法同样旨在通过最少的函数值计算次数来达到较高的搜索效率。 #### 三、逼近方法 除了区间消去法之外，还有另外一类方法被称为逼近方法，这些方法通过构建函数的近似模型来逼近最优解。主要方法包括： - **曲线插值法**：通过拟合多项式或其它形式的函数来逼近原函数，从而寻找最优解。 - **二次逼近法**：使用二次多项式来拟合目标函数，进而确定最优解。 - **三次逼近法**：利用三次多项式来拟合目标函数，寻找最优解。 - **牛顿法**：基于函数的一阶和二阶导数信息来构建局部二次逼近模型。 - **割线法**：类似于牛顿法，但不需要计算二阶导数，而是使用函数值和一阶导数值来更新近似模型。 #### 四、划界法 划界法是一种通过设置上下界来限定最优解范围的方法。例如，可以通过构造一系列上界和下界的函数来逼近最优解，直到满足预定义的精度要求。 ### 总结 本文详细介绍了几种常见的精确一维搜索方法，包括对分法、等间隔搜索法以及Fibonacci法和黄金分割法等对称区间搜索法。这些方法各有特点，适用于不同的情形。在实际应用中，选择合适的搜索方法对于提高搜索效率至关重要。同时，了解每种方法的优点和局限性有助于更有效地解决实际问题。