三值逻辑函数的基本表式及其Karnaugh图分析

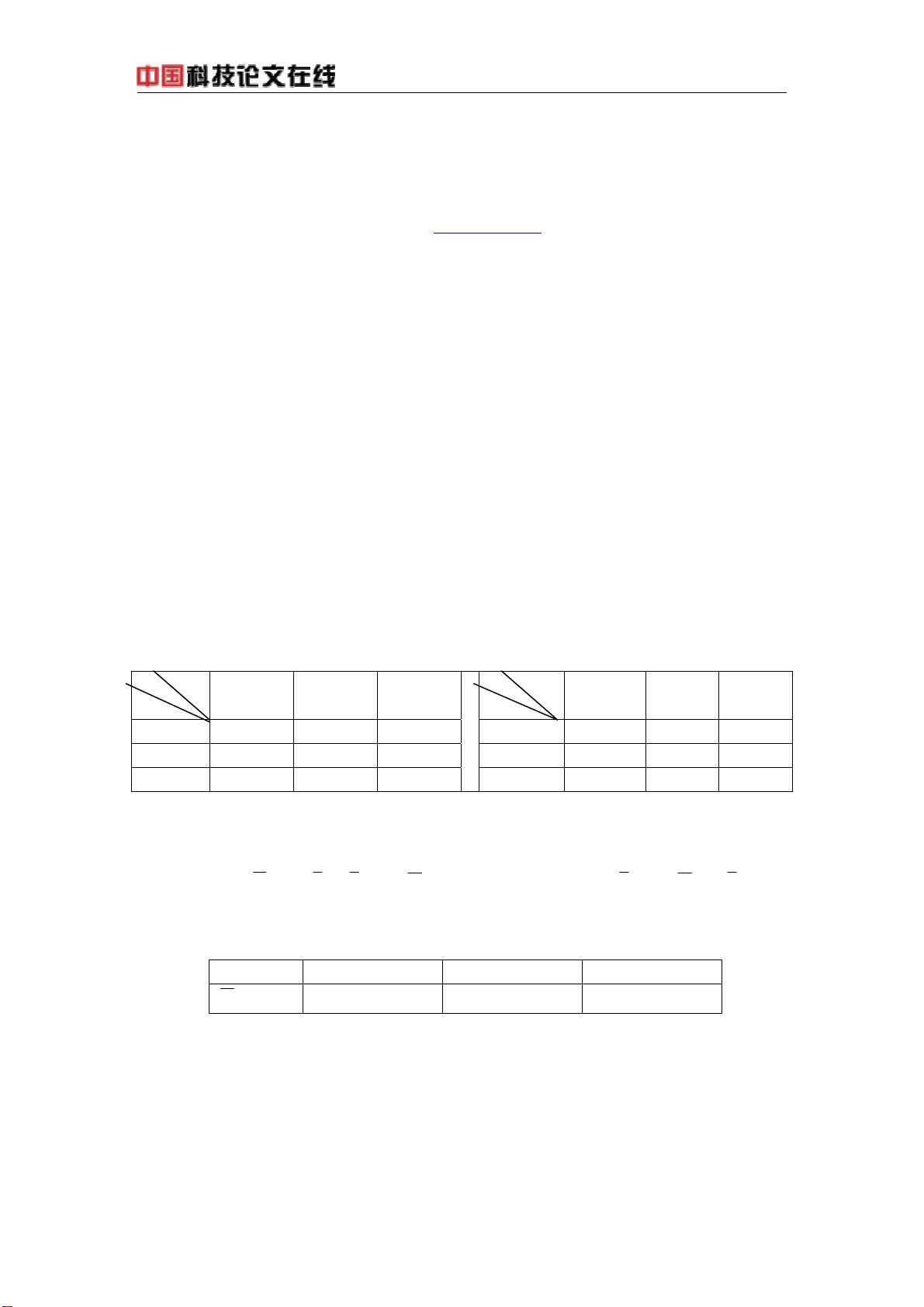
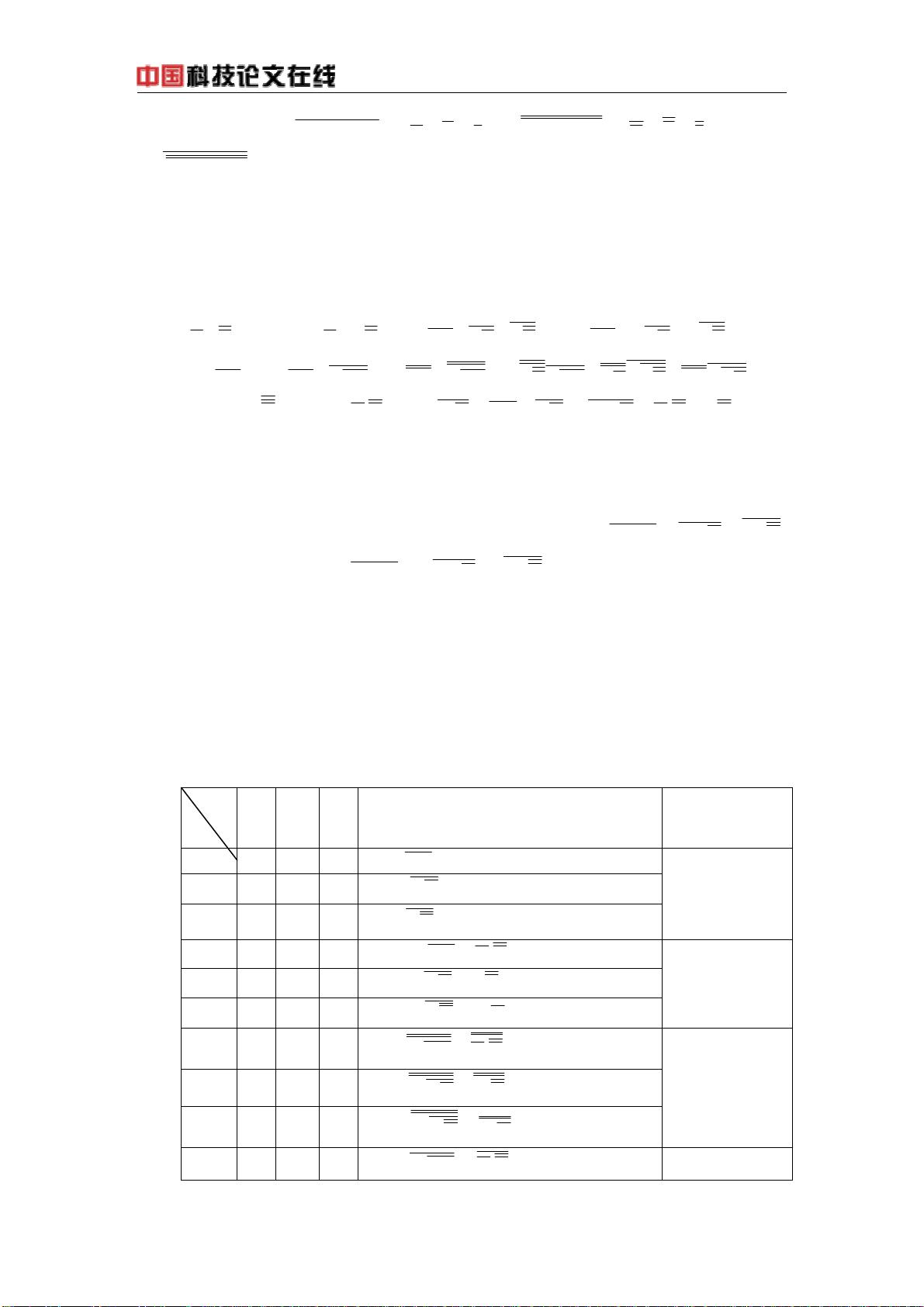
三值逻辑是逻辑学的一个分支，它扩展了传统的二值逻辑，允许变量取三个可能的值而不是两个。二值逻辑中的每个变量只能是0或1，代表真和假，而在三值逻辑中，第三个值通常表示不确定或部分真/假的状态。J.Lukasiewicz和E.L.Post是最早对三值逻辑进行研究的学者之一，他们为逻辑值“假”、“乏晰”和“真”分别指定了数值“0”、“1”和“2”，或者使用“0”、“Φ”和“1”来表示，其中“Φ”代表中间状态。 三值逻辑函数涉及的是三值逻辑变量之间的关系，这种关系可以用函数表示。一个三值逻辑函数的表示式能够穷举单变量的所有可能性，并对这些可能性进行分析。单变量三值逻辑函数有27种可能的表示式，这是由于每个变量可以取三个值，所以函数的输出也有三种可能。这些表示式可以用来建立一个表格，表中每一行代表一个特定的函数。 Karnaugh图是一种图形化的工具，用于简化和可视化布尔逻辑函数，它也可以应用于三值逻辑函数。在三值逻辑的上下文中，Karnaugh图的形状被设计为正八面形，以适应三个逻辑状态。它有助于直观化地展示逻辑函数的简化过程，特别是用于找出相邻项以合并它们，从而简化函数表达式。 本文作者李裕信探讨了三值逻辑函数的基本表式，并设计了一种正八面形的Karnaugh图来表达这些函数。文章中提到了三种衍生的二值逻辑变量，这些变量是由三值逻辑系统衍生出来的，尽管在三值逻辑系统中不存在传统的布尔逻辑中的“非”运算，但可以通过三值逻辑的其他运算来表达相似的功能。 作者还提出了m元三值逻辑函数个数的计算公式，这是分析逻辑函数复杂性的重要一步。对于二变量三值逻辑函数，其数目是19683个，而它们的Karnaugh图具有极高的复杂性，其主要框架是由多个6顶点完全图及正八面形组成的图形，这表明了二变量函数复杂度之高以及其可能的层次结构。 在三值逻辑系统中，与二值逻辑相似的“或”和“与”运算被定义，但还有其他的运算，比如“转移”运算。这个运算的真值表被给出，以帮助理解三值逻辑中变量是如何相互作用的。转移运算展示了三值逻辑变量之间的关系，它允许在逻辑表达式中进行替代和简化。 文章指出，一个独立的三值逻辑变量，如果不附加任何条件，则不存在布尔代数中的“逻辑非”运算。这意味着，在三值逻辑系统中，不能简单地将一个逻辑值取反以得到其否定值，因为逻辑状态“Φ”代表了一种既不为0也不为1的模糊状态。 通过文章中提到的恒等式，我们可以了解三值逻辑系统中运算的规则，例如并项律和转移律。这些规则与布尔逻辑中的德摩根定律类似，它们定义了运算之间的基本关系，并且可以通过真值表得到验证。 在三值逻辑代数中，一个变量的函数可以表示为三个基底的线性组合，即任何单变量的三值逻辑函数都可以用三个基底函数的和来表达，而这些基底函数是通过变量和逻辑值“Φ”组合而成。这样，函数的每个项都对应于这些基底函数的一个系数，这些系数可以是三个值中的任一个。 总而言之，三值逻辑提供了一种处理逻辑问题的更丰富框架，尤其适用于那些需要表示不确定状态或者中间状态的领域。通过对三值逻辑函数的基本表式及其Karnaugh图的深入分析，能够更好地理解和应用三值逻辑系统，同时为复杂系统的设计和优化提供理论支持。