在sNN=2.76TeV时PbPb碰撞中（1S），ϒ（2S）和ϒ（3S）夸克态的抑制资源-CSDN文库

Open

Access

196 浏览量 2020-05-06 02:04:15 上传评论收藏 989KB PDF 举报

资源推荐

资源详情

资源评论

Physics Letters B 770 (2017) 357–379

Contents lists available at ScienceDirect

Physics Letters B

www.elsevier.com/locate/physletb

Suppression of ϒ(1S), ϒ(2S), and ϒ(3S) quarkonium states in PbPb

collisions at

√

= 2.76 TeV

.The CMS Collaboration



CERN, Switzerland

a r t i c l e i n f o a b s t r a c t

Article history:

Received

4 November 2016

Received

in revised form 26 March 2017

Accepted

13 April 2017

Available

online 19 April 2017

Editor:

M. Doser

Keywords:

CMS

Physics

Heavy

ions

Dimuons

Bottomonia

The production yields of ϒ(1S), ϒ(2S), and ϒ(3S) quarkonium states are measured through their decays

into muon pairs in the CMS detector, in PbPb and pp collisions at the centre-of-mass energy per nucleon

pair of 2.76 TeV. The data correspond to integrated luminosities of 166 μb

−1

and 5.4 pb

−1

for PbPb and

pp collisions, respectively. Differential production cross sections are reported as functions of ϒ rapidity

y up to 2.4, and transverse momentum p

up to 20 GeV/c. A strong centrality-dependent suppression is

observed in PbPb relative to pp collisions, by factors of up to ≈2and 8, for the ϒ(1S) and ϒ (2S) states,

respectively. No signiﬁcant dependence of this suppression is observed as a function of y or p

. The ϒ (3S)

state is not observed in PbPb collisions, which corresponds to a suppression for the centrality-integrated

data by at least a factor of ≈7at a 95% conﬁdence level. The observed suppression is in agreement with

theoretical scenarios modeling the sequential melting of quarkonium states in a quark gluon plasma.

(http://creativecommons.org/licenses/by/4.0/). Funded by SCOAP

1. Introduction

At large energy density and high temperature, strongly interact-

ing

matter is predicted by lattice QCD calculations to consist of a

deconﬁned system of quarks and gluons [1]. This state, often re-

ferred

to as “quark gluon plasma” (QGP) [2], constitutes the main

object of studies using high energy heavy ion collisions.

The formation of QGP in nuclear collisions is studied in a va-

riety

of ways. One of its most striking signatures is the sequential

suppression of quarkonium states, both in the charmonium (J/ψ,



, χ

, etc.) and the bottomonium (ϒ(1S, 2S, 3S), χ

, etc.) fami-

lies.

Historically, this phenomenon was proposed as direct evidence

of deconﬁnement because, in the deconﬁned medium, the binding

potential between the constituents of a quarkonium state, a heavy

quark and its antiquark (QQ), should be screened by the colour

charges of the surrounding light quarks and gluons [3,4]. The sup-

pression

of quarkonium production is predicted to occur above the

critical temperature of the medium (T

) and to depend on the

QQbinding energy. Since the ϒ(1S) is the most tightly bound state

among all quarkonia, it is expected to have the highest dissocia-

tion

temperature. Estimates of dissociation temperatures are given

in Ref. [5]: T

dissoc

≈ 2 T

, 1.2 T

, and 1 T

for the ϒ(1S), ϒ(2S),

and ϒ(3S) states, respectively. Other medium effects, such as re-

generation

from initially uncorrelated quark–antiquark pairs [6,7]



E-mail address: cms-publication-committee-chair@cern.ch.

or absorption by comoving particles [8,9] can modify quarkonium

production in heavy ion collisions. Furthermore, nuclear effects

such as modiﬁcations of parton distributions inside nuclei [10]

energy loss processes in nuclear matter [11] are expected to

affect the production of quarkonia independently of any QGP for-

mation.

An admixture of several of the above-mentioned effects in

the context of bottomonium production is investigated in Refs. [12,

13] and

a recent review on quarkonium production can be found

in Ref. [14].

The suppression of ϒ(1S) production in heavy ion collisions rel-

ative

to pp yields scaled by the number of binary nucleon–nucleon

(NN) collisions was ﬁrst measured by CMS [15] in the midrapidity

range |y| < 2.4, then by ALICE at forward rapidities 2.5 < y < 4

[16].

Both measurements were done at the CERN LHC in PbPb

collisions at a centre-of-mass energy per nucleon pair,

√

, of

2.76 TeV. Alarger suppression of the ϒ(2S) and ϒ(3S) was ﬁrst

suggested [17] then observed [18] by CMS. In pPb collisions at

√

= 5.02 TeV, ALICE [19] and LHCb [20] reported ϒ(1S) yields

that are slightly suppressed along the p-going forward direction,

possibly indicating the importance of nuclear effects. Lacking pp

reference data at

√

= 5.02 TeV, the pp yields were estimated

by interpolating results at 2.76, 7, and 8TeV [19], or by scaling

data at 8TeV [20]. The ϒ(2S) and ϒ(3S) were reported by CMS

to be slightly more suppressed than the ϒ(1S) ground state in

pPb collisions [21]. At the BNL RHIC, STAR reported no signiﬁcant

suppression of the overlapping ϒ(1S +2S +3S) states in dAu colli-

sions

√

= 200 GeV, while observing a suppression in central

http://dx.doi.org/10.1016/j.physletb.2017.04.031

0370-2693/

SCOAP

358 The CMS Collaboration / Physics Letters B 770 (2017) 357–379

AuAu collisions at the same energy [22]. Altogether, these results

are interpreted as a sequential suppression of the three states in

nucleus–nucleus collisions [12,13], with the tighter bound states

disappearing less in the QGP.

This Letter reports the production yields of ϒ(1S), ϒ(2S), and

ϒ(3S) for PbPb and pp data at the same

√

= 2.76 TeV, using

integrated luminosities of 166 μb

−1

and 5.4 pb

−1

, respectively. The

two sets of data correspond to approximately the same number of

NN collisions. The pp sample collected in 2013 contains 20 times

more events than the 2011 data used previously [15,17,18], allow-

ing

further differential studies with respect to the ϒ meson rapid-

ity

and transverse momentum. Muon reconstruction is improved in

PbPb collisions relative to Ref. [18], yielding a 35% increase in the

number of measured ϒ candidates. In total, the improved recon-

struction

and a relaxed muon-p

selection provide almost twice

the number of ϒ(1S) candidates used in Ref. [18]. The yields in

PbPb and pp events are used to extract nuclear modiﬁcation fac-

tors,

2. The CMS detector

A detailed description of the CMS detector, together with a def-

inition

of the coordinate system used and the relevant kinematic

variables, can be found in Ref. [23]. The central feature of the CMS

apparatus is a superconducting solenoid of 6m internal diameter.

A silicon tracker, a crystal electromagnetic calorimeter, and a brass

and scintillator hadron calorimeter reside within the magnetic ﬁeld

volume.

Muons

are detected in the pseudorapidity interval |η| < 2.4

using

gas-ionization detectors made of three technologies: drift

tubes, cathode strip chambers, and resistive-plate chambers, em-

bedded

in the steel ﬂux-return yoke of the solenoid. The silicon

tracker is composed of pixel detectors (three barrel layers and two

forward disks on either side of the detector, made of 66 million

100×150 μm

pixels) followed by microstrip detectors (ten barrel

layers, and three inner and nine forward disks on either side of the

detector, with strips of pitch between 80 and 180 μm). The trans-

verse

momentum of muons matched to tracks reconstructed in the

silicon detector is measured with a resolution better than 1.5% for

values smaller than 100 GeV/c [24]. This high resolution is the

result of the 3.8 T magnetic ﬁeld and the high granularity of the

silicon tracker.

addition, CMS has extensive forward calorimetry, includ-

ing

two steel and quartz-ﬁbre Cherenkov hadron forward (HF)

calorimeters, that cover the range 2.9 < |η| < 5.2. These detectors

are used in the present analysis to select events and to determine

the centrality of PbPb collisions, as described in the next section.

3. Data selections

3.1. Event selection and centrality

To select purely inelastic hadronic PbPb collisions, contributions

from ultraperipheral collisions and noncollision beam backgrounds

are removed, as described in Ref. [25]. Events are preselected if

they contain a primary vertex built from at least two tracks, and

at least three signals (one in the case of pp collisions) in HF tow-

ers

on each side of the interaction point with deposited energies of

at least 3GeV in each tower. To further suppress beam-gas events,

the distribution of hits in the pixel detector along the beam direc-

tion

is required to be compatible with particles originating from

the event vertex. These criteria select (97 ± 3)%of the inelas-

tic

hadronic PbPb collisions [25], yielding an eﬃciency-corrected

number of minimum bias (MB) events N

= (1.16 ± 0.04) × 10

for the MB sample corresponding to this analysis. The pp data

Table 1

Average

values of the number of participating nucleons (N

part

, with the root-mean-

square

of its distribution in each bin), and nuclear overlap function (T

, with its

systematic uncertainty) for the centrality bins used in the ϒ(1S) (upper rows) and

ϒ(2S) (middle) analyses. The centrality-integrated values are given in the last row.

Centrality (%) N

part

 (RMS) T

 (mb

−1

)

0–5 381 (19) 25.9 ±1.1

5–10 329 (22) 20.5

±0.9

10–20 261 (30) 14.5

±0.8

20–30 187 (23) 8.80

±0.58

30–40 130 (18) 5.09

±0.43

40–50 86.2 (13.6) 2.75

±0.30

50–70 42.0 (14.4) 0.98

±0.14

70–100 8.8 (6.0) 0.125

±0.023

0–10 355 (33) 23.2

±1.0

10–30 224 (46) 11.6

±0.7

30–50 108 (27) 3.92

±0.37

50–100 22.1 (19.3) 0.47

±0.07

0–100 113 (115) 5.67

±0.32

correspond to an integrated luminosity of 5.4 pb

−1

, known to an

accuracy of 3.7% coming from the uncertainty in the calibration

based on a van der Meer scan [26].

The

measurements are based on events that were ﬁrst selected

by the Level-1 trigger, a hardware-based system that uses informa-

tion

from the muon detectors and calorimeters. The presence of at

least two muons was required, with no selection applied on their

momenta. The events were then further ﬁltered using a software-

based

high-level trigger, and rejected if muons were poorly recon-

structed,

hence likely to be misidentiﬁed. The pp and PbPb data

were collected using the same trigger logic.

The

centrality of PbPb collisions is deﬁned as the fraction of

the total number of inelastic hadronic collisions, with 0% repre-

senting

collisions with the largest overlap of the two nuclei. This

fraction is determined from the distribution of total energy in both

HF calorimeters. Variables related to the centrality, such as the

number of nucleons participating in the collision (N

part

) and the

nuclear overlap function (T

) [27], are estimated using a Glauber

model simulation described in Ref. [25]. The value of T

at a

given centrality is equal to the number of binary NN collisions

divided by the NN cross section and can be interpreted as the NN-

equivalent

integrated luminosity per heavy ion collision.

is to be noted that the PbPb hadronic cross section (7.65 ±

0.42 b) computed with this Glauber simulation corresponds to an

integrated luminosity of 152 ±9 μb

−1

, compatible within 1.2 sigma

with the experimental value of 166 ± 8 μb

−1

based on the van der

Meer scan. The mean values of T

and N

part

are presented in Ta-

ble 1 for

the narrow centrality bins used in the ϒ(1S) analysis,

the wider bins used in the ϒ(2S) analysis, and the centrality-

integrated

estimate. The most peripheral bins are rather wide

and, since quarkonium yields scale with the number of nucleon–

nucleon

collisions, most bottomonia are produced close to the

most central edge of the bins, namely 70% and 50%. The N

part



values shown in the following ﬁgures and reported in Table 1 are

computed by averaging over all MB events in a given centrality bin,

and are therefore not corrected for any bias introduced by requir-

ing

the presence of the ϒ . Also presented is the root-mean-square

(RMS) of the N

part

distribution in each bin. The uncertainty on T

is computed by varying the Glauber parameters and the event se-

lection

ineﬃciency, as described in Ref. [25]. In this Letter, N

part



is used to show the centrality dependence of the measurements,

while T

directly enters into the nuclear modiﬁcation factor cal-

culation:

= N

PbPb





where N

PbPb

is the number of ϒ

produced per PbPb collision in a given kinematic range and σ

the corresponding ϒ cross section in pp collisions.

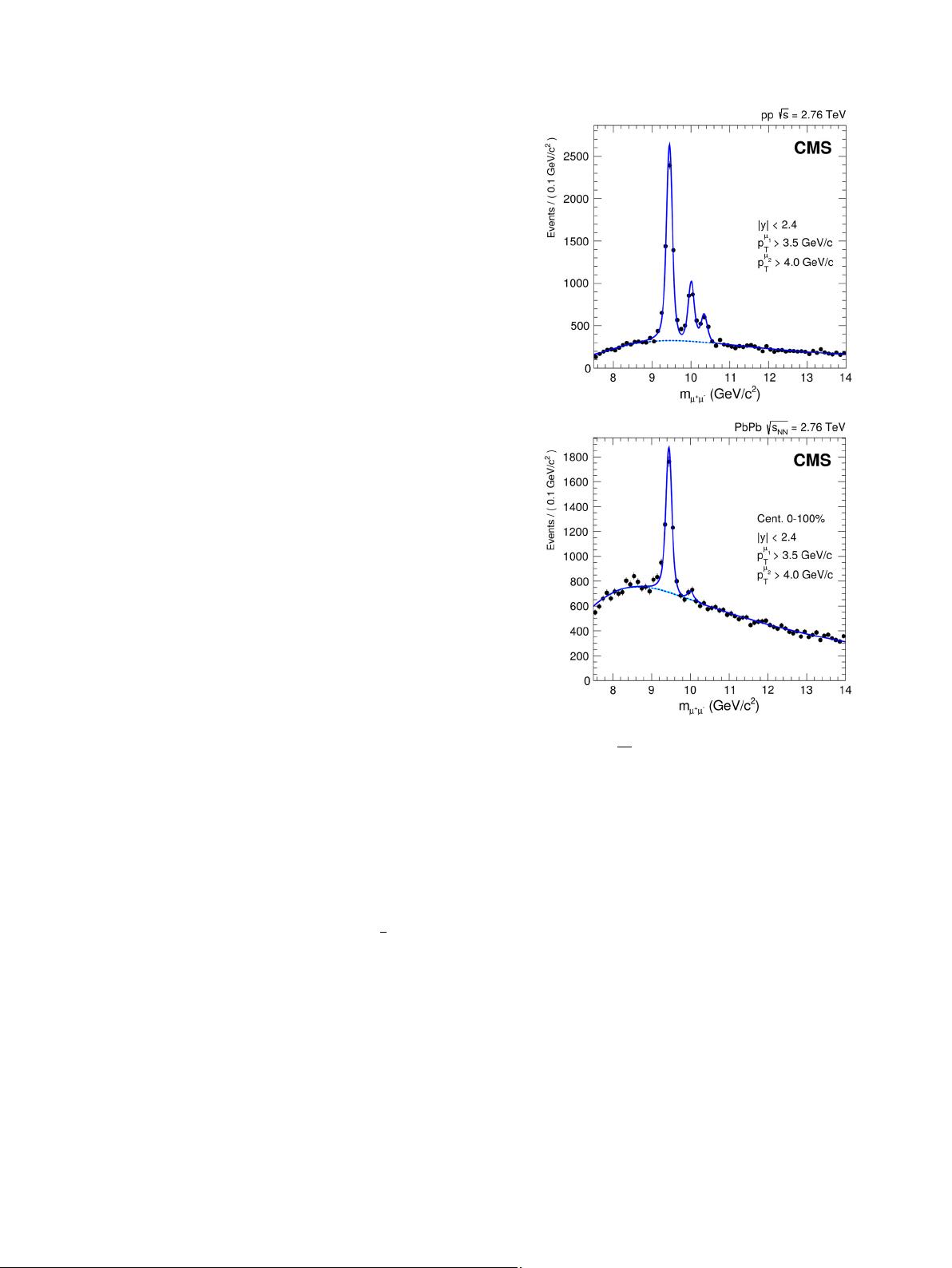
The CMS Collaboration / Physics Letters B 770 (2017) 357–379 359

3.2. Muon selection

Muons are reconstructed using a global ﬁt to a track in the

muon detectors that is matched to a track in the silicon tracker.

The oﬄine muon reconstruction algorithm used for the PbPb data

has been improved relative to that used previously [18]. The

eﬃciency has been increased by running multiple iterations in

the pattern recognition step, raising the number of reconstructed

ϒ(1S) candidates by approximately 35%. Background muons from

cosmic rays and heavy-quark semileptonic decays are rejected by

imposing a set of selection criteria on each muon track. These

criteria are based on previous studies of the performance of the

muon reconstruction algorithm [28]. The track is required to have

a hit in at least one pixel detector layer, and a respective transverse

(longitudinal) distance of closest approach of less than 3 (15) cm

from the measured primary vertex, primarily to reject cosmic ray

muons and muons from hadron decays in ﬂight. To ensure a good

measurement, more than 10 hits are requested in the tracker,

and the χ

per number of degrees of freedom of the trajectory

ﬁts is limited to be smaller than 10 when using the silicon tracker

and the muon detectors, and smaller than 4 when using only the

tracker. Pairs of oppositely charged muons are considered when

the χ

ﬁt probability of the tracks originating from a common ver-

tex

exceeds 1%.

For

the ϒ(2S) and ϒ(3S) analyses, the transverse momentum

of each muon (p

) is required to be above 4 GeV/c, as in previ-

ous

publications [15,17,18], while one of them is relaxed down to

3.5 GeV/c for the ϒ(1S) analysis. Reducing this p

threshold raises

the ϒ(1S) yield by approximately 40%, and its statistical signiﬁ-

cance

by up to 50%, depending on the p

and y of the dimuon

system. Relaxing the criterion on the second muon was also con-

sidered

then discarded, since it did not signiﬁcantly raise the ac-

ceptance

for the ϒ states. The resulting invariant mass distribu-

tions

are shown on Fig. 1 for the entire pp and PbPb data samples.

4. Analysis

4.1. Signal extraction

To extract the ϒ(1S), ϒ(2S), and ϒ(3S) meson yields, unbinned

maximum likelihood ﬁts to the μ

−

invariant mass spectra are

performed between 7.5 and 14 GeV/c

. The results for the p

-, y-

and

centrality-integrated case are displayed as solid lines on Fig. 1.

Each ϒ resonance is modelled by the sum of two Crystal Ball (CB)

functions [29] with common mean but different widths to account

for the pseudorapidity dependence of the muon momentum res-

olution.

The CB functions are Gaussian resolution functions with

the low-side tail replaced by a power law describing ﬁnal-state ra-

diation.

This choice was guided by simulation studies, as well as

analyses of large pp event samples collected at

√

s = 7 TeV [30].

Given the relatively large statistical uncertainties, the only signal

model parameters that are left free in the ﬁt are the mean of the

ϒ(1S) peak, and the ϒ(1S), ϒ(2S) and ϒ(3S) meson yields. The

other parameters, such as the width of the ϒ(1S) peak are ﬁxed

in every bin to the corresponding value obtained from simulations.

The mean and width of the CB functions describing the ϒ(2S) and

ϒ(3S) peaks are set by the ﬁtted ϒ(1S) peak mean and the ﬁxed

ϒ(1S) width, respectively, multiplied by the world-average mass

ratio [31]. The parameters describing the tail of the CB function

are ﬁxed to values obtained from simulations, kept common in

the three ϒ states, then allowed to vary when computing the as-

sociated

systematic uncertainties. The background distribution is

modelled by an exponential function multiplied by an error func-

tion

(the integral of a Gaussian) describing the low-mass turn-on,

with all parameters left free in the ﬁt.

Fig. 1. Dimuon invariant mass distributions in pp (top) and centrality-integrated

PbPb (bottom) data at

√

= 2.76 TeV, for muon pairs having one p

greater than

4 GeV/c and the other greater than 3.5 GeV/c. The solid (signal + background) and

dashed (background only) lines show the result of ﬁts described in the text.

With one muon having p

greater than 4 GeV/c and the other

greater than 3.5 GeV/c, this ﬁtting procedure results in ϒ(1S) me-

son

yields and statistical uncertainties of 2534 ±76 and 5014 ±87

centrality-integrated PbPb and pp collisions, respectively. With

both muons’ transverse momenta above 4 GeV/c, it yields 173 ±41

for

ϒ(2S) and 7 ±38 for ϒ(3S) (hence unobserved) in PbPb colli-

sions,

and 1214 ± 51 for ϒ(2S) and 618 ± 44 for ϒ(3S) states in

pp collisions.

4.2. Acceptance and eﬃciency

To correct yields for acceptance and eﬃciency in the two

data samples, the three ϒ states have been simulated using the

pythia 6.412

generator [32] and embedded in PbPb events sim-

ulated

with hydjet 1.8 [33], producing Monte Carlo (MC) events

with the same settings as in Ref. [18], including radiative tails

handled by photos [34]. Acceptance is deﬁned as the fraction of

ϒ in the |y| < 2.4range that decay into two muons, each with

|η

| < 2.4, and p

> 4 GeV/c and p

> 3.5or 4 GeV/c for the

ϒ(1S) and ϒ(2S)/ϒ(3S) states, respectively. For the ϒ(1S) state,

the acceptance over the analyzed phase space averages to 35%. For

all three ϒ states, the acceptance is constant over most of the ra-

pidity

range, with a drop at large |y|. When the ϒ meson has

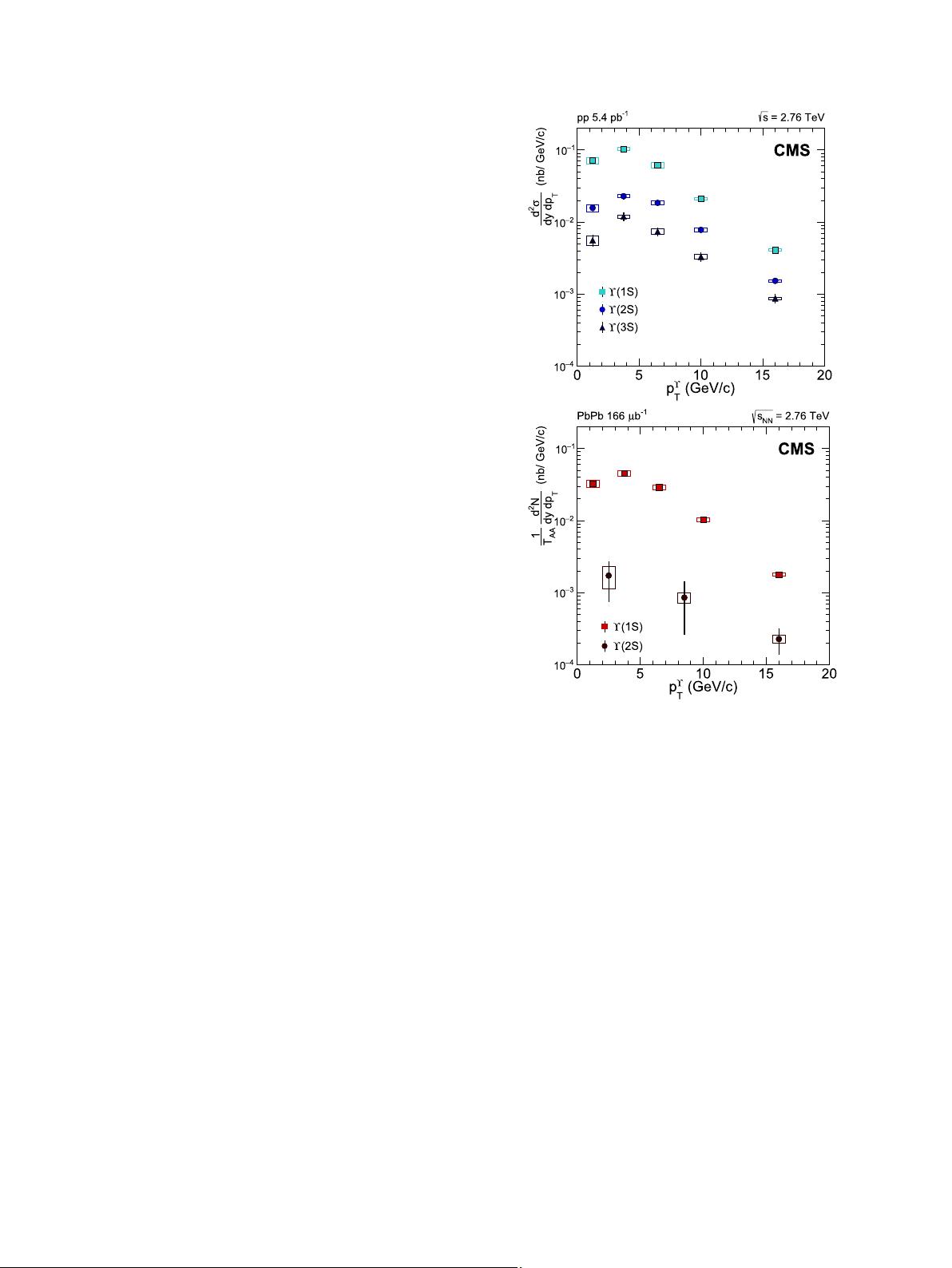
360 The CMS Collaboration / Physics Letters B 770 (2017) 357–379

≈ 5 GeV/c, the lower p

decay muon often falls below the re-

quired

momentum to reach the muon detector, resulting in a drop

in acceptance for intermediate p

. For ϒ(2S) and ϒ(3S) states,

where p

for both muons is required to be above 4 GeV/c, the ac-

ceptance

is 28 and 33%, respectively. Within this acceptance, the

average reconstruction and trigger eﬃciencies are 68, 74 and 75%

for the ϒ(1S), ϒ(2S), and ϒ(3S) states, respectively. The slightly

lower eﬃciency for the ϒ(1S) state arises from including lower-p

muons, which have smaller reconstruction eﬃciencies, in particu-

lar

at midrapidity.

The

individual components of the eﬃciency are crosschecked

using collision data and muons from J/ψ meson decays, with a

technique called tag-and-probe, similar to the one described in

Ref. [30]. The method consists of ﬁtting the J/ψ candidates in

data and MC samples, with and without applying the probed se-

lection

criterion on one of the muons. The muon reconstruction,

identiﬁcation, and trigger eﬃciencies in the muon detectors are

probed by testing the selection response in a sample collected

with single-muon triggers. The small discrepancies observed be-

tween

the results for data and simulation are used to determine

- and η-dependent single-muon correction factors that are ap-

plied

to muons in the simulation. The net correction factors to the

ϒ meson yields range from 3 to 18%, the largest being located

at low p

or at large |y|. The tracker eﬃciency, larger than 99%,

is also evaluated with this method by checking the presence of a

track for muons that are primarily reconstructed in the muon de-

tectors.

The corresponding uncertainty is evaluated to be 0.3 and

0.6% for each muon, for the pp and PbPb data, respectively.

4.3. Systematic uncertainties

The uncertainty from the ﬁtting procedure is estimated by per-

forming

seven changes in the ﬁtting functions. Five of them consist

of releasing one by one the originally ﬁxed signal-shape parame-

ters,

to accommodate for possible imperfections in the simulation.

The other two changes consist of adding to the default background

function a ﬁrst- or second-order Chebychev polynomial. The max-

ima

of the ﬁve signal and of the two background variations are

summed in quadrature, yielding systematic uncertainties from 4 to

25% in the PbPb data and from 1 to 10% in the pp data, for the

ϒ(1S) meson yield. For the less signiﬁcant ϒ(2S) signal, the un-

certainties

range from 13 to 71% in PbPb, and from 1 to 15% in pp

data.

The

systematic uncertainty from the acceptance and eﬃciency

estimation includes changes of the generated p

and y spectra, as

well as variations of the distribution of ϒ candidates across event

centrality, within limits imposed by the data themselves. These are

propagated into bin-by-bin systematic uncertainties of 0.7 and 1.1%

on average, in pp and PbPb collisions, respectively.

Single-muon

eﬃciencies obtained from the tag-and-probe

method

are assigned a systematic uncertainty from varying re-

quirements

for the tag selection, the dimuon mass range, and

the distributions of the invariant mass peak and the underlying

backgrounds. The maximum deviation in each p

and η

inter-

val

is retained as the systematic uncertainty on the single-muon

correction factors. Next, the single-muon correction factors are

changed within their statistical uncertainties derived from data. To

do so, one hundred variations of the single-muon eﬃciencies are

computed, resulting in one hundred dimuon eﬃciency correction

factors in each analysis bin. The RMS of the resulting eﬃcien-

cies,

summed in quadrature with the systematic uncertainty in the

eﬃciency correction factors, represent the overall uncertainty in

muon eﬃciency. The resulting systematic uncertainties range from

3.2 to 7.7% from midrapidity in pp collisions to the most forward

bins in PbPb collisions. In addition, the uncertainty in the tracking

Fig. 2. Differential cross section for ϒ states as a function of their transverse mo-

mentum

and per unit of rapidity in pp (top) and PbPb (bottom) collisions. The PbPb

results are integrated over centrality and divided by the number of elementary NN

collisions. Statistical (systematic) uncertainties are displayed as error bars (boxes).

Global relative uncertainties of 3.7% (pp) and 6.5% (PbPb) are not displayed.

eﬃciency of 0.3 and 0.6% for each track is considered as fully cor-

and thus doubled for dimuon candidates, and taken as a

global uncertainty (common to all points).

The

relative uncertainties in the integrated luminosity of pp

data (3.7%) or the number of PbPb MB events (3%) are also con-

sidered

as global uncertainties. The uncertainties in the T

values

are given in Table 1.

5. Results

5.1. Cross sections

Figs. 2 and 3 show the differential cross sections as functions

of p

(per unit of rapidity) and |y|, respectively, in pp (top) and

PbPb (bottom) collisions. Measured yields are corrected for the ac-

ceptance

and eﬃciency, then divided by the width of the bin in

consideration. To put the pp and PbPb data on a comparable scale,

the corrected yields are normalized by the measured integrated

luminosity in pp collisions, and by the product of the number of

corresponding MB events and the centrality-integrated T

value

for PbPb collisions. The statistical uncertainties in pp collisions al-

low

a measurement for the three states using the same binning:

ﬁve bins in p

with edges at 0, 2.5, 5.0, 8.0, 12.0, and 20.0 GeV/c,

剩余22页未读，继续阅读

评论收藏

内容反馈

weixin_38737630

粉丝: 1
资源: 929

在sNN = 2.76TeV时PbPb碰撞中（1S），ϒ（2S）和ϒ（3S）夸克态的抑制

最新资源

在sNN = 2.76TeV时PbPb碰撞中（1S），ϒ（2S）和ϒ（3S）夸克态的抑制

在TeV的PbPb碰撞中ϒ（1S），ϒ（2S）和ϒ（3S）介子的核修饰因子的测量

在sNN = 2.76 TeV的PbPb碰撞中的射流形状的修改

J / Ïˆ抑制在sNN = 2.76 TeV时Pb–Pb碰撞中的中心性，速度和横向动量依赖性

在sNN = 2.76 TeV时中心Pb-Pb碰撞中的射流抑制量

在sNN = 2.76 TeV时PbPb碰撞中即时和非即时J /ψ产生的抑制和方位各向异性

CMS实验在sNN = 2.76TeV时超外围PbPb碰撞中的相干J /ψ产生

来自美强子衰变的电子的椭圆流是从$$ \ sqrt {s_ \ mathrm {NN}} = 2.76 \ \ hbox {TeV} $$ sNN = 2.76TeV的Pb–Pb碰撞数据中提取的

在sNN = 2.76TeV时，pp和Pb–Pb碰撞中快中性产生中性离子

在sNN = 2.76 TeV时Pb-Pb碰撞中带电粒子各向异性流的伪快速依赖关系

相干Ïˆ（2S）照片生产在sNN = 2.76 TeV的超外围Pb Pb碰撞中

在sNN = 5.02 TeV的p–Pb碰撞中产生clusive（1S）和ϒ（2S）

sNN = 2.76 TeV Pb–Pb碰撞中带电射流产生的方位各向异性

在sNN = 5.02 TeV的pPb碰撞中的魅力射流截面和核修饰因子的测量。

在sNN = 2.76 TeV处在中央Pb–Pb碰撞中搜索弱衰减的α›nâ和α›异源结合态

在$$ \ sqrt {s_ \ mathrm {NN}} = 2.76 $$ sNN = 2.76 TeV的Pb–Pb碰撞中，前向速度的$$ \ phi $$介子产生

在sNN = 2.76 TeV的Pb-Pb碰撞中的H› 3和Hâ€›β3生产

在sNN = 2.76 TeV的pp和Pb–Pb碰撞中，在较大的横向动量处产生带电的离子，钾和质子

$$ \ text {Pb--Pb} $$ Pb--Pb碰撞在$$ \ sqrt {s_ \ mathrm {{NN}}} = 2.76 \ hbox {TeV} $$ sNN = 2.76TeV

200 GeV Au-Au和2.76 TeV Pb-Pb碰撞中的Dihadron方位角相关性

Ï•-前向速度的介子生产在sNN = 5.02 TeV处的p–Pb碰撞中和在s = 2.76 TeV处的pp碰撞中

更正为“在Pb处于中等快速度的多奇异重子产生” – sNN = 2.76 TeV时的Pb碰撞– [物理。 来吧 B 728（2014）216-227]

在sNN = 5.02 TeV时Pb-Pb碰撞中带电粒子的伪快速密度分布的中心依赖性

pPb碰撞中sNN = 5.02 TeV时横向能量密度的中心性和拟快速性依赖性

J / Ïˆ抑制sNN = 5.02 TeV下Pb–Pb碰撞中的前向速度

最新资源

更正为“在Pb处于中等快速度的多奇异重子产生” – sNN = 2.76 TeV时的Pb碰撞– [物理。来吧 B 728（2014）216-227]