没有合适的资源?快使用搜索试试~ 我知道了~
Non-Hermitian degeneracies of internal–external mode pairs in di...
0 下载量 8 浏览量
2021-02-22
07:44:34
上传
评论
收藏 2.41MB PDF 举报
温馨提示
Open quantum and wave systems can exhibit non-Hermitian degeneracies called exceptional points, where both the eigenvalues and the corresponding eigenstates coalesce. Previously, such exceptional points have been investigated in dielectric microcavities in terms of optical modes which are well confined inside the cavity. However, beside these so-called “internal modes” with a relatively high quality factor, there exists another kind of mode called “external modes,” which have a large decay rate
资源推荐
资源详情
资源评论

Non-Hermitian degeneracies of internal–external
mode pairs in dielectric microdisks
CHANG-HWAN YI,
1
JULIUS KULLIG,
1,2
MARTINA HENTSCHEL,
2
AND JAN WIERSIG
1,
*
1
Institut für Physik, Otto-von-Guericke-Universität Magdeburg, Postfach 4120, D-39016 Magdeburg, Germany
2
Institut für Physik, Technische Universität Ilmenau, D-98693 Ilmenau, Germany
*Corresponding author: jan.wiersig@ovgu.de
Received 22 January 2019; revised 19 February 2019; accepted 19 February 2019; posted 19 February 2019 (Doc. ID 357992);
published 25 March 2019
Open quantum and wave systems can exhibit non-Hermitian degeneracies called exceptional points, where both
the eigenvalues and the corresponding eigenstates coalesce. Previously, such exceptional points have been inves-
tigated in dielectric microcavities in terms of optical modes which are well confined inside the cavity. However,
beside these so-called “internal modes” with a relatively high quality factor, there exists another kind of mode
called “external modes,” which have a large decay rate and almost zero intensity inside the cavity. In the present
paper, we demonstrate the physical significance of the external modes via the occurrence of exceptional points of
internal–external mode pairs for transverse electric polarization. Our numerical studies show that these excep-
tional points can be achieved by either a boundary deformation of the microdisk or by introducing absorption
into a circular cavity.
© 2019 Chinese Laser Press
https://doi.org/10.1364/PRJ.7.000464
1. INTRODUCTION
Openness is a generic property of realistic quantum and wave
systems. Hence, their dynamics is in general described by a
non-Hermitian Hamiltonian with complex eigenvalues. An
interesting feature of this non-Hermitian physics is the excep-
tional point (EP) in parameter space where both the eigenvalues
(complex frequencies) and the corresponding eigenstates
(modes) coalesce [1–3]. So far, EPs have been studied both
theoretically and experimentally in various research fields such
as hydrogen atoms [4], photonic lattices [5], microlasers [6,7],
microwave resonators [8–10], and optical microcavities [11–14].
One of the fascinating applications of EPs is an enhancement of
the sensitivity of sensors [15–19].
Optical microdisk cavities are ideal model systems to study
non-Hermitian physics [20]. In recent years, it was demon-
strated that EPs in microcavities can be caused by several mech-
anisms, e.g., by boundary deformations [12,21–24] or external
perturbations like nanoscatterers or nanofiber tips [11,13,25].
However, in these studies, the involved modes are always so-
called internal modes whose intensity is well confined inside
the cavity, resulting in a small decay rate, i.e., a large Q-factor.
In the language of formal quantum mechanics, they are called
Feshbach resonances [26–28].
Along with the internal modes, there is another class of
optical modes known as “external modes,” which have a large
decay rate and almost no intensity inside the cavity. The
internal and external modes have been classified in previous
studies [28–30] according to their behavior in the limit of
infinite refractive index n; i.e., in the limit of vanishing open-
ness of the system. In this limit, the external modes remain
unbound and are therefore referred to as “shape resonances”
[26–28]. The internal modes, however, can become bound
states with real-valued frequency in this limit.
In spite of the pioneer works proving the interactions
between internal and external modes [30], there have been
no investigations conceiving the possibility of EPs associated
with external modes. Therefore, the aim of this paper is to re-
veal the existence of such EPs involving internal and external
mode pairs. To demonstrate this, we introduce two kinds of
systematic perturbations of a circular cavity: (i) a deformation
of the cavity’
s boundary, and (ii) an absorbing material.
The paper is organized as follows. In Section 2, the optical
modes of the dielectric microdisk cavity are briefly explained. In
Section 3, a transition between the strong and weak coupling
regime in the circular cavity is analyzed. Section 4 demonstrates
EPs through the variation of a deformation parameter. In
Section 5, absorption is used to generate EPs in the circular
cavity. Section 6 summarizes and concludes the paper.
2. MODES IN THE DIELECTRIC MICRODISK
For the convenience of the reader, we repeat some known facts
of optical modes in quasi-two-dimensional microdisks [20].
The damped time-harmonic solutions of Maxwell’s equations
in the dielectric microdisk cavity with effective refractive index
464
Vol. 7, No. 4 / April 2019 / Photonics Research
Research Article
2327-9125/19/040464-09 Journal © 2019 Chinese Laser Press
n and Sommerfeld’s outgoing-wave condition at infinity are the
optical modes. On the cavity boundary interfacing the homo-
geneous refractive index regions, the two dif ferent polarization
fields, transverse magnetic fTM: E
z
x, y, tReψx, ye
−iωt
g
and transverse electric fTE: H
z
x, y, tReψx, ye
−iωt
g,
with resonant frequency ω, satisfy different boundary condi-
tions; ∂
ν
ψ (1∕n
2
∂
ν
ψ) is continuous for TM (TE) polarization,
while ψ for both polarizations is continuous across the
boundary. Here, E
z
H
z
is the z-component of the electric
(magnetic) field and ∂
ν
is the normal derivative at a given
boundary point .
Through the separation of variables in polar coordinates, the
optical modes in the circular cavity with radius R are given by a
dimensionless frequency kR ωR∕c ∈ C (where c is the speed
of light in vacuum), which are the solutions of the radial
equation [26]
η
J
0
m
J
m
nkR −
H
0
m
H
m
kR0, (1)
where J, J
0
, H, and H
0
are the Bessel functi on, its derivative,
the Hankel function of the first kind, and its derivative, respec-
tively, and η n (1∕n) for TM (TE) polarization. Note that
the obtained modes are specified by an azimuthal mode num-
ber m [i.e., the order of Bessel functions in Eq. (1)] and a radial
mode number l labeling the solutions of Eq. (1) for fixed m.
Note also that the modes given by the solutions of Eq. (1) are
doubly degenerated for m ≠ 0 since they are invariant under
the change of m and −m.
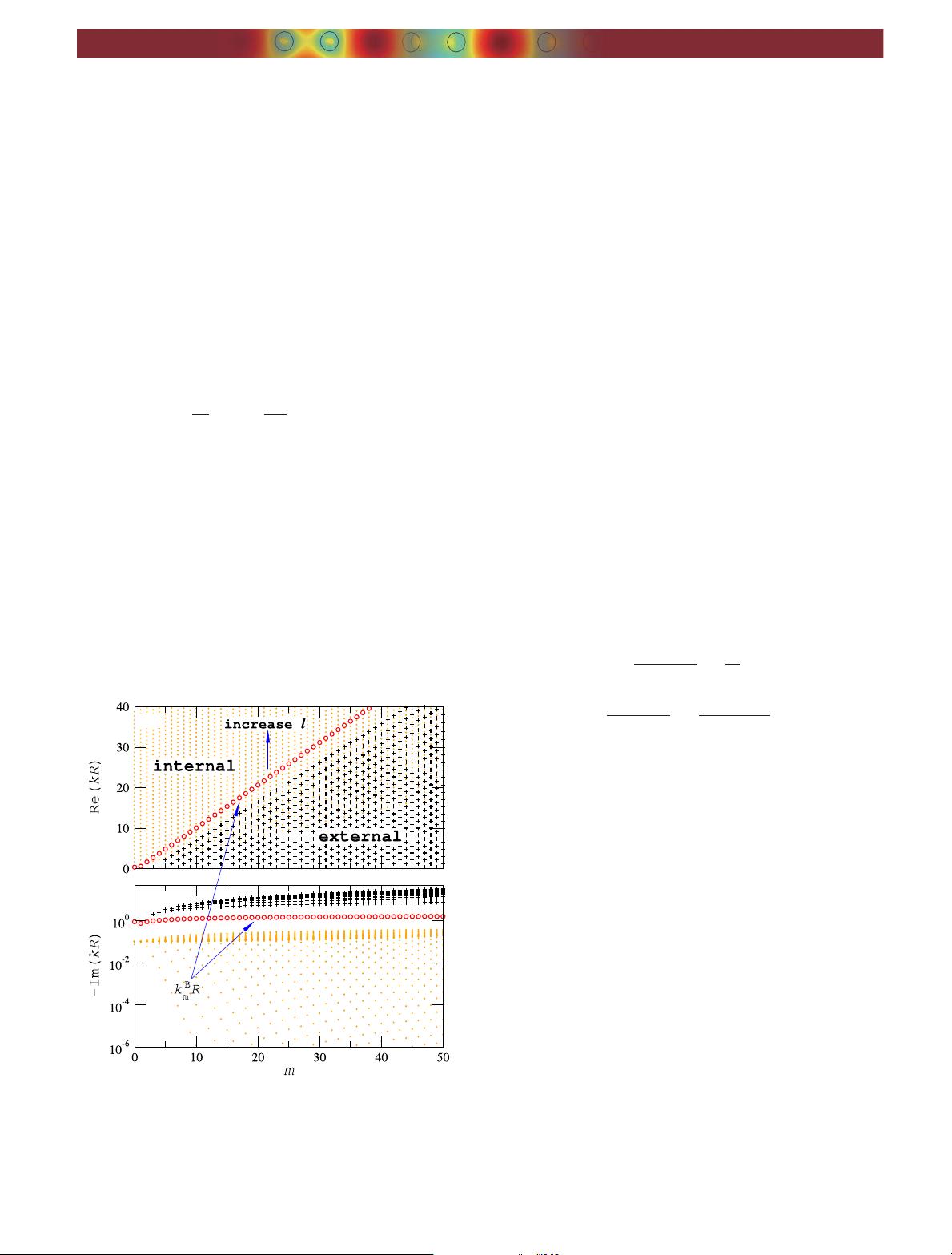
Figure 1 shows the optical modes as the solution of Eq. (1)
for TE polarization with refractive index n 3.14. Among the
modes in the figure, the internal and external modes are clearly
discerned by the imaginary part of the frequency [see Fig. 1(b)]:
while the internal modes have small values of jImkR j < 1,
the external modes have jImkRj > 1. In between these two
distinct mode groups, we can observe an additional group of
special external modes with jImkRj ≈ 1 existing only for
TE polarization. These modes are attributed to the Brewster
angle [31,32], and thus we call them Brewster modes with their
frequencies k
B
m
R. A perfect transmittance at this Brewster angle
(but see [33] for the curved interface correction) results in ro-
bust coupling of internal–external modes [30]. In order to take
advantage of this coupling, we focus on the TE polarization in
the present paper. We emphasize that the radial mode number l
should be treated carefully when discerning internal and exter-
nal modes; while in the former case, l counts the number of
maxima of the mode intensity along the radial direction inside
the cavity, and l of the external modes has no corresponding
physical interpretation [28]. Thus, whenever we specify the
mode numbers l, m, we refer to internal modes.
3. WEAK AND STRONG COUPLI NG OF MODES
IN CIRCULAR CAVITIES
In this section, we consider a circular cavity with a real-valued
refractive index n. For the internal modes, nRek
m
R is approx-
imately constant. Thus, if n changes, the frequency k
m
needs
to shift accordingly. Contrarily, the external modes correspond-
ing to the Brewster angle fulfill the relation Rek
B
m
R ≈
m
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 n
−2
p
[26,32]. Hence, the derivatives of the frequencies
with respect to n read
dRek
m
R
dn
∼ −
1
n
2
, (2a)
dRek
B
m
R
dn
∼ −
1
n
2
ffiffiffiffiffiffiffiffiffiffiffiffiffi
n
2
1
p
: (2b)
Equations (2a) and (2b) indicate that Rek
m
R of the internal
modes decreases more rapidly than Rek
B
m
R as n increases.
Hence, Rek
B
m
R with a fixed azimuthal mode number m suc-
cessively degenerates with different values of Rek
m
R having
higher values of l. We define the degree of degeneracy in terms
of the real part of the frequencies:
Δ
−1
≡ jRek
B
m
R − Rek
I
m
R
−1
j, (3)
between the modes with frequencies k
B
m
R and k
I
m
R. The
latter of these is defined to be the frequency of the internal
mode whose real part is the nearest to the real part of the
Brewster mode’s frequency for a fixed m. The degenerate points
appear as peaks in Fig. 2 that display the degree of degeneracy as
a function of refractive index n and m for several values of radial
mode number l.
It is an interesting fact that even in the circular cavity, sig-
natures of an EP can be observed in the parameter space
spanned by the real-valued refractive index and the radial mode
number l. However, it is important to mention that this EP
cannot be reached exactly because l is a discrete variable.
Similar to the studies in Refs. [12,21] on deformed cavities,
the EP rather manifests in a narrow transition region between
the two different coupling regimes: weak and strong coupling.
(a)
(b)
Fig. 1. (a) Real and (b) imaginary part of scaled frequency kR of the
modes in the microdisk obtained by Eq. (1) for TE polarization with
n 3.14, as a function of azimuthal mode number m. Dots (·), crosses
(+), and open circles (∘) mark internal modes, external modes, and k
B
m
R
corresponding to the Brewster angle, respectively.
Research Article
Vol. 7, No. 4 / April 2019 / Photonics Research 465
剩余8页未读,继续阅读
资源评论

weixin_38733355
- 粉丝: 4
- 资源: 897
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功