没有合适的资源?快使用搜索试试~ 我知道了~
提出了一种新的时空通用MUSIC(TS-GMUSIC)方法用于低海拔目标的高度测量。 作为传统时空过程的扩展,我们提出的方法采用交替投影(AP)理论来测量目标高程。 与将方向矢量迭代投影以实现仰角的常规AP不同,我们将接收到的回波迭代投影到不同的信号子空间上以获得仰角。 因此,可以将多个目标的常规方向搜索简化为一个目标参数估计。 此外,我们考虑了低海拔目标的多径几何特征,因此将直接波和镜面波的方向搜索更改为一维参数搜索。 蒙特卡洛仿真证明,提出的TS-GMUSIC比现有的时空算法表现出更好的性能。 此外,甚高频雷达的实时数据处理证明了该方法的有效性。
资源推荐
资源详情
资源评论

Altitude Measurement Based
on Beam Split and Frequency
Diversity in VHF Radar
BAIXIAO CHEN
GUANGHUI ZHAO
SHOUHONG ZHANG
Xidian University
China
A new beam split altitude interferometry based on altitude
diversity and frequency diversity for very high frequency (VHF)
radar is proposed in this paper. As opposed to microwave rada r,
VHF radar has a wide beam which is usually split when ground
reflection occurs. The reflected wave which is coherent with the
direct wave will always be contained in the target echo. In this
paper, several antennas of different heights are utilized. Owing to
the certain relationship among the phases of the split beams, the
elevation region where the targets are located can be determined
using the phases of echoes. Using “amplitude-comparison”
of echoes from various antennas to get the normalized error
signals, the elevation of the target can be obtained by looking
it up in the error signal table. The effect of roughness on the
altitude measurement accuracy is also analyzed. The real data
processing on flat and slope terrains testifies to the validity of the
proposed method. The altitude measurement precision, especially
in low-elevation regions, is greatly improved by using frequency
diversity.
Manuscript received September 17, 2006; revised August 2, 2007,
January 26, May 27, and July 11, 2008; released for publication
July 18, 2008.
IEEE Log No. T-AES/46/1/935925.
Refereeing of this contribution was handled by P. Lombardo.
This work was supported by the National Science Foundation of
China under Grant 60772068 and the Program for New Century
Excellent Talents in University under Grant NCET-06-0856.
Authors’ addresses: B. Chen and S. Zhang, National Lab for Radar
Signal Processing, Xidian University, Xi’an, Shaanxi, China; G.
Zhao, Intelligent Perception and Image Understanding Key Lab of
Ministry of Education, Xidian University, Xi’an, Shannxi 710071,
China, E-mail: (ghzhao@mail.xidian.edu.cn).
0018-9251/10/$26.00
c
° 2010 IEEE
I. INTRODUCTION
With the rapid development of concealment and
ARM (antiradiation missile) technology, current radar
often experiences difficulties in tracking low-flying
targets, i.e., targets that are within a beamwidth of
the horizon. The difficulty is due to the reflections
from the surface of the Earth. In general, the
reflected energy consists of the specular and diffuse
components. The specular component is usually more
difficult to deal with since it is by far the stronger
of the two; it is highly correlated with the direct
component, and it also lies within the beamwidth
of the receiving antenna. Thus, detecting the target
of low altitude and avoiding the influence of the
multipath are becoming more challenging. Nakatsuka
[1] and Zoltowski [2] introduce multiple beams to
separate the paths respectively. Recently Boman [3]
presents a new low-angle target-tracking method
with comprehensive target models. Considering
the complex reflection over the sea, E. Bosse [4]
investigates the Swerling fluctuating targets tracking.
Recently array signal processing has been used in this
field, and much effort has been spent in developing
high-resolution techniques for direction-of-arrival
(DOA) estimation of multiple signals [5—7]. These
methods, such as the multiple signal classification
(MUSIC) [8] algorithm, min-norm [9] algorithm, are
based on the subspace, which can provide an excellent
performance at high signal-to-noise ratio (SNR), long
data records, and in a spatially uncorrelated sources
field. However, when some of the signals are fully
coherent, e.g., when the target flies at a low altitude,
the echo received contains multipath signals, and
these techniques encounter serious difficulties. The
maximum likelihood (ML) [10] method, which is
based on analyzing the joint probability distribution
of received data, can be used in the case of coherent
signals with better statistical performance than
MUSIC. However, more computation is required,
which restricts the ML algorithm from practical
applications. Motivated by computational efficiency
and the need for real-time tracking, a number of ML
estimation schemes have been proposed for low-angle
radar tracking [11]. Some other methods based on
multifrequency tracking are also underdeveloped
[4, 12]. In this paper, we propose a new method for
altitude measurement based on beam split.
In 1939, an American made the first radar, CXAM,
that could estimate the altitude of a target by using
the multipath signals. The performance of this radar is
greatly affected by many aspects such as the condition
of the sea, the reflection of the atmosphere, and the
SCR of the target. During World War II, a new set of
radar called CH was built in England which measures
the altitude of a target by comparing the amplitude
of the main beams of two receiving antennas. By
switching in aerials mounted at different heights above
IEEE TRANSACTIONS ON AEROSPACE AND ELECTRONIC SYSTEMS VOL. 46, NO. 1 JANUARY 2010 3
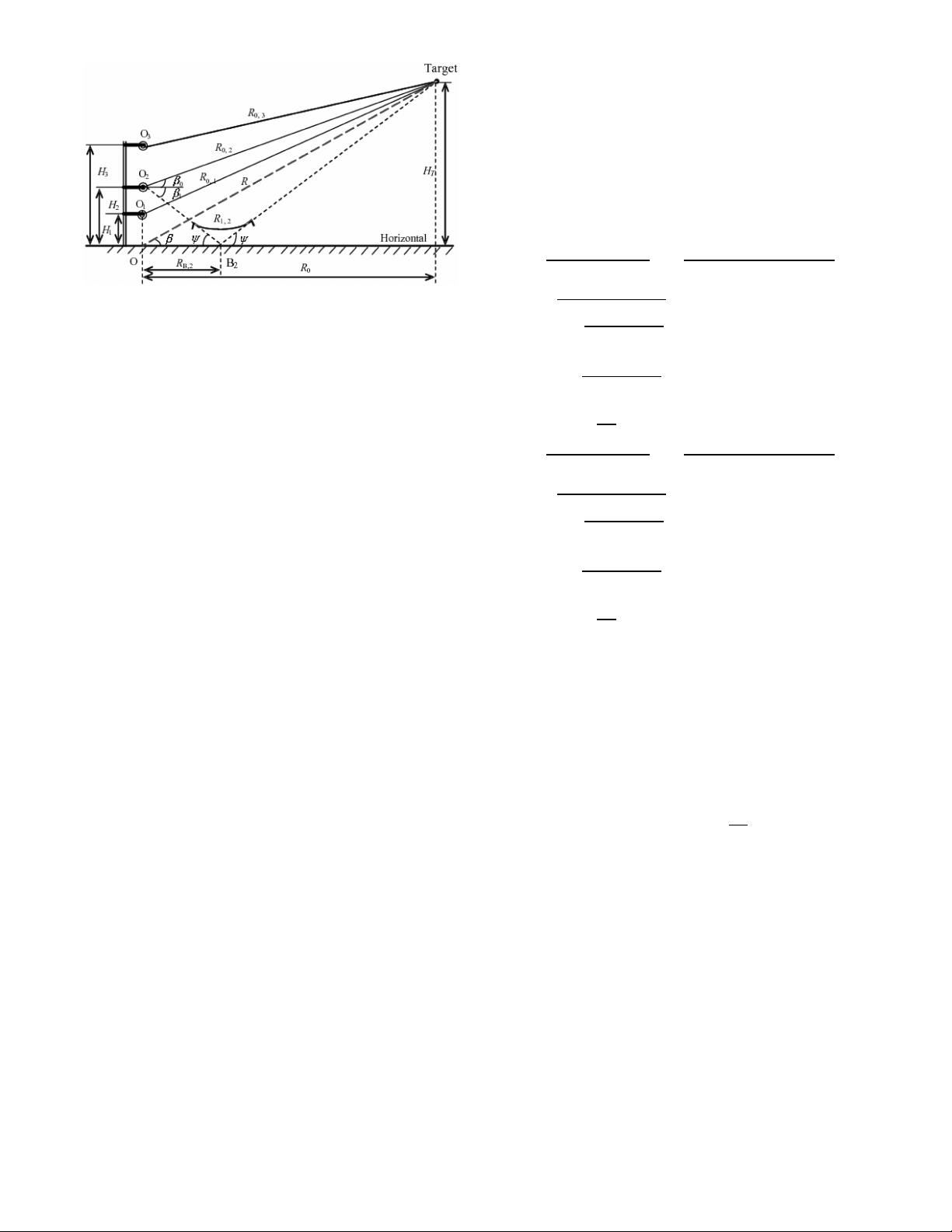
Fig. 1. Multipath geometry for low-altitude target in flat plane.
the ground, the angle of elevation of the echo signal
is assessed, and when combined (automatically by
an electrical calculator) with the measured range,
the aircraft’s height is calculated [13]. However, the
method is inapplicable when the target flies low in the
far field.
Because of its long wavelength, very high
frequency (VHF) r adar has particular advantages
in anticoncealment and anti-ARM. Recently much
attention has again been paid to the development of
VHF radar [14] systems all over the world. However,
thewidebeamofVHFradarwillbesplitdueto
the ground reflection, so this kind of radar can only
be used to estimate altitude roughly. It has been a
challenge to enhance the capability of VHF radar to
measure altitude accurately.
Many methods have been developed to avoid the
effect of multipath, an effect which, on the contrary,
is employed here. Because antennas at dif ferent
heights have different split beams that are related
to one another in phase, we adopt what we call a
“phase and amplitude comparison” [15] method to
measure the altitude. This paper presents the principle
of this method in detail, and analyzes its performance
and the influence of surface roughness. Finally both
simulation and experimental results are presented.
The paper is organized as follows. In Section II
we present the beam split phenomenon. In Section III
we propose the method for altitude measurement
based on beam split in VHF radar. In Section IV we
analyze the performance of the method. In Section V
we present the influence of SNR on the accuracy of
altitude measurement. In Section VI the experimental
results are given. And in Section VII a brief summary
is made.
II. BEAM SPLIT PHENOMENON
A beam must be sensiti ve to elevation when it is
used to measure altitude. It is possible for VHF radar
to measure altitude because beam split makes each
beam narrow. More than one antenna should be used
because we cannot decide which beam the echo is
in with only one receive antenna. Here three sets of
antennas located in high, medium, and low positions
are used to measure altitude. As shown in Fig. 1, O
1
,
O
2
,andO
3
are the three receiving antennas whose
heights are H
1
, H
2
,andH
3
, respectively, while the
transmit antenna is placed next to O
2
. Suppose that
the height of the target is H
T
, the elevation is ¯,and
the horizontal distance from the target to the antenna
is R
0
. We can then obtain H
T
= R
0
tan ¯ À H
i
and
R
2
= R
2
0
+ H
2
T
. According to geometry,
R
0,i
=
q
R
2
0
+(H
T
¡ H
i
)
2
=
q
R
2
0
+ H
2
T
+ H
2
i
¡ 2H
T
H
i
= R
s
1+
H
2
i
¡ 2H
T
H
i
R
2
¼ R
μ
1+
H
2
i
¡ 2H
T
H
i
2R
2
¶
(* H
i
¿ H
T
)
¼ R
μ
1 ¡ H
i
H
T
R
2
¶
= R ¡ H
i
sin¯, i = 1—3 (1)
R
1,i
=
q
R
2
0
+(H
T
+ H
i
)
2
=
q
R
2
0
+ H
2
T
+ H
2
i
+2H
T
H
i
= R
s
1+
H
2
i
+2H
T
H
i
R
2
¼ R
μ
1+
H
2
i
+2H
T
H
i
2R
2
¶
(* H
i
¿ H
T
)
¼ R
μ
1+H
i
H
T
R
2
¶
= R + H
i
sin¯, i = 1—3 (2)
where R
0,i
denotes the direct path and R
1,i
(i =1,2,3)
the multipath.
The d ifference between R
0,i
and R
1,i
is
d
R,i
= R
1,i
¡ R
0,i
¼ 2H
i
sin¯: (3)
Taking the influence of the reflected wave into
consideration, the pattern with respect to elev ation ¯
is
F
i
(¯)=F(¯
0
)+¡F(¯
i
)exp
μ
¡j
4¼
¸
H
i
sin¯
¶
(4)
where ¸ is the wavelength and ¡ = ½
r
exp(jÁ
r
)isthe
reflectance of ground. For horizontal polarization
and flat ground, ¡ = ¡1, ½
r
=1,Á
r
= ¼; F(¯)isthe
elevation pattern function without considering the
influence of the reflected wave, and the antenna is
composed of 8 log periodic dipole antenna elements
of horizontal polarization. Fig. 2 is the elevation
pattern of direct wave of one of the antennas, where
the longest element length is 1.5 m, the shortest
element length is 0.5 m, the scaling factor ¿ is 0.86,
andthespacingfactor¾ is 0.1. ¯
0
and ¯
1
are the
direction of the direct wave and the reflected wave,
respectively. For wide beam, the gain is approximately
constant, i.e., F(¯
0
) ¼ F(¯
1
), in the vicinity of zero
degree. In far field, if the antenna is far lower than the
4 IEEE TRANSACTIONS ON AEROSPACE AND ELECTRONIC SYSTEMS VOL. 46, NO. 1 JANUARY 2010
剩余10页未读,继续阅读
资源评论

weixin_38731027
- 粉丝: 4
- 资源: 975
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 基于Python的南京二手房数据采集及可视化分析.zip
- 大数据采集、抽取平台,zdh-web是zdh系列服务的可视化管理平台,包含数据采集、调度、权限、导航流、私域营销等模块.zip
- 基于注意力的多尺度卷积神经网络轴承故障诊断 针对传统方法在噪声环境下诊断精度低的问题,提出了一种多尺度卷积神经网络的滚动轴承故障诊断方法 首先,构建多尺度卷积提取不同尺度的故障特征,同时引入通道注意
- 常用文本匹配模型tf版本,数据集为QA-corpus,持续更新中.zip
- 安卓项目源码Android安卓游戏打地鼠源码
- 开放旋转机械故障数据集(旋转机械开源故障数据集整理).zip
- 机械设计新能源电池管壳组装线体sw18非常好的设计图纸100%好用.zip
- 开源SFT数据集整理、随时补充.zip
- 安卓项目源码Android仓库管理系统源码
- 机械设计轧机机架step非常好的设计图纸100%好用.zip
- 微信HOOK、微信机器人wxhook,数据库解密微信公众号采集微信公众号爬虫,企业微信HOOK.zip
- 安卓项目源码Android操作数据库实例
- C++实现斗地主游戏:包含玩家、牌型与出牌规则
- musetalk嘴型同步
- JLINK V9插入电脑没反应
- 安卓项目源码Android城市天气预报源码
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功