极速消失极限时消失的水平Kerr-AdS黑洞资源-CSDN文库

Open

Access

167 浏览量 2020-03-24 02:19:20 上传评论收藏 727KB PDF 举报

资源推荐

资源详情

资源评论

JHEP01(2018)042

Published for SISSA by Springer

Received: September 10, 2017

Accepted: December 23, 2017

Published: January 10, 2018

Extremal vanishing horizon Kerr-AdS black holes at

ultraspinning limit

S.M. Noorbakhsh

and M.H. Vahidinia

b,c

Science Beam Institute,

P.O. Box 19848-35367, Tehran, Iran

School of Physics, Institute for Research in Fundamental Sciences (IPM),

P.O. Box 19395-5531, Tehran, Iran

Research Institute for Ast ronomy and Astrophysi cs of Maragha (RIAAM),

Maragha 55 134 -4 41, Iran

E-mail:

maryam@sciencebeam.com, vahidinia@ipm.ir

Abstract: By utilizing the ultraspinning limit we generate a new class of extremal van-

ishing horizon (EVH) black holes in odd dimensions (d ≥ 5). Starting from the general

multi-spinning Kerr-AdS metrics, we show the EVH limit commutes with the ultr asp i nni ng

limit,in which the resulting solutions possess a non-compact but ﬁn i te area manifold for all

(t, r 6= r

) = const . slices . We also demonstrate the near horizon geometries of obtained

ultraspinning EVH solutions contain an AdS

throats, whe r e it would be a BTZ black hole

in the ne ar EVH cases. The commutativity of the ultraspinning and near horizon limits

for EVH solutions is conﬁrmed as well. Furthermore, we discuss only ﬁve-dimensional case

near the EVH point can be vi ewed as a super-entropic black hole. We also show that

the thermodynamics of the obtained solutions agree wi t h the BTZ black hole. Moreover

we investigate the EVH/CFT proposal, demonstrating the entropy of 2d dual CFT and

Bekenstein-Hawking entropy are equivalent.

Keywords: Black Holes, AdS-CFT Cor r es pondence

ArXiv ePrint:

1708.08654

Open Access,

 The Authors.

Article funded by SCOAP

https://doi.org/10.1007/JHEP01(2018)042

JHEP01(2018)042

Its extensions in the presence of the cosmological c onst ant were introduced in four and

ﬁve dimensions by [

2] and [3]. Furthermore, the general multi-spinning spinning Kerr-AdS

(KAdS) and Ker r -dS solutions in all higher dimension d have been found in [

4, 5]. They

also extended their solution by assuming NUT charges in [

6]. It is shown that, for d ≥ 6,

the rot ati n g asymptotically ﬂat black holes may have arbitrary large angular momentum

with the ﬁxed mass by sending the rotation parameter to inﬁn i ty (a → ∞) [

1]. So they are

referred as ultr aspi nn i ng (US) black holes.

Not only US limit may be utilized to study instability of rotating black holes at large

angular momentum [

7], but also preforming these limits lead to nontrivial and new interest-

ing geometr i e s. In particular , for asymptotically AdS black holes, a variety of solutions can

be generated corresponding with how the rotation parameter a reaches to the AdS radius

l. For example , by taking a → l l i mi t, while either the physical mass or horizon radius is

kept ﬁxed , the resulting geometry would be a black brane [8] or hyperboloid membrane [9].

In addition, there is another recipe that is applicable to asymptotically (A)dS black holes,

in which both a and l go to inﬁni ty while their ratio is ﬁni t e [

10].

Recently a n ew ultraspinning limit was introduced by [11] such that the generating

black hole solutions exhibit a distinguished property which is a noncompact horizon with a

ﬁnite area. Similar solutions have been found in the context of Einstein-Maxwell-Λ theory

and N = 2 gauged supergravity coupled to vector multiplets by [

12]. This novel ultraspin-

ning limit can be viewed as a simple generating black hole solution technique in the presence

of the cosmological constant. Several authors have appl i ed this metho d to construct new

black hole solutions from multi-spinning Kerr-AdS black holes (KAdS) [

13], four and ﬁve-

dimensional gauged supergravity solutions [

14] and higher dimensional charged AdS black

holes [

15]. In all cases, the re sul t i ng new exact black hole possess a non-compact horizon

with ﬁnite entropy, that topologically describes a sphere with some punctures.

Moreover, by ex am i ni ng the behavior of the mentioned new US black holes in the

extended thermodyn ami c phase space, it was shown that they may violate the Reverse

Isoperimetric Ineq ual i ty in some range of parameters [

16]. This inequality implies an upper

bound on the horizon area (Bekenstein-Hawking entropy) of a black hole with a certai n ther-

modynamic volume.

Therefore, si n ce the entropy of these family of US black holes exceed

their corresponding maximum entropy, this limit is also cal l ed super-entropic limit [

11, 13].

Extremality is another interesting limit of black holes and black branes whose sur-

face gravity vanishes. Curiously, in this limit black holes (branes) represent near hori zon

geometries that not only they belong to a new class of (non-black holes) solutions, but

also possesses an enhanced symmetry. For example , extremal p-branes in supergravity

admit AdS

p+1

subspace, while the regular extremal black holes generically have an AdS

sector in the near horizon geometry [

17, 18]. Interes ti n gl y enough, st udy i ng them led to

AdS/CFT [

19] and Kerr/CFT (Extremal/CFT), respectively [20, 21]. There are some

uniqueness and existence theorems about the near horizon geometry of extremal black

holes [

18, 22–25]. Meanwhile, these geometries represent a nice ( the r mo) dy nami c behav-

It was shown that (charged) Schwarzschild-AdS black hole has a maximum entropy for a given

volume [

16].

– 2 –

JHEP01(2018)042

ior [26, 27]. Some features about the near horizon of extremal black holes strongly depend

on smoothness of the horizon. However, there is a particular class of them with non-smooth

horizon. Among them t he r e is a particular family with vanishing horizon, that their hori-

zon area approach to zero linearly with temperature A

∝ T → 0, near the extremal poi nt.

Also the vanishing of the horizon area is a result of vani shi n g one-cycle on the hori z on.

Therefore, they are usually cal l ed Extremal Vanishin g Horizon (EVH) black holes [

28–42].

Near horizon limit of EVHs also provides a new class of solutions and they enjoy an

enhanced symmet r y. It has been proved that the EVH black holes in Einst i e n-M ax well-

Dilaton-Λ gravity admit a three-d i me nsi onal maximally symmetr i c subspace in the near

horizon. In the case of Einstei n -Λ with negative cosmological constant, this subspace

would be an AdS

. For a near EVH (NEVH) black hole, where the entropy and the

temperature are small but non zero, the AdS

will be replaced by a BTZ black hole [43–45].

Recently, it was shown in [

42] that in the case of EVH Ke r r -dS black holes, this 3d part can

interpolat e between dS

, ﬂat and AdS

spaces depending on rotation parameters, while the

near horizon of an EVH cosmological soliton al ways present a dS

. Appearing the AdS

sector in the near horizon of EVH solutions suggests that low energy physics on t he EVH

geometries may have a dual holographic descript i on in terms of a CFT

. This duality is

usually called EVH/CF T correspondence [

43].

The interesting features of EVH and ultraspinning black holes, motivated us to mix

EVH and US limits on a given metric by taking diﬀerent orders. The primary purpose

of this work is investigating if t he ultraspinni ng black holes have a well-deﬁned EVH de-

scription, and exploring EVH conﬁgurations from ultraspinning black holes. Since EVH

black holes suﬀer a singularity on the horizon, we also were curious to examine whether

the US limit can lead to gett i ng rid of this problem. For these purposes, we will c onsi d er

the general multi-spinning Kerr-AdS (KAdS) black holes in all dimensions. Then by ex-

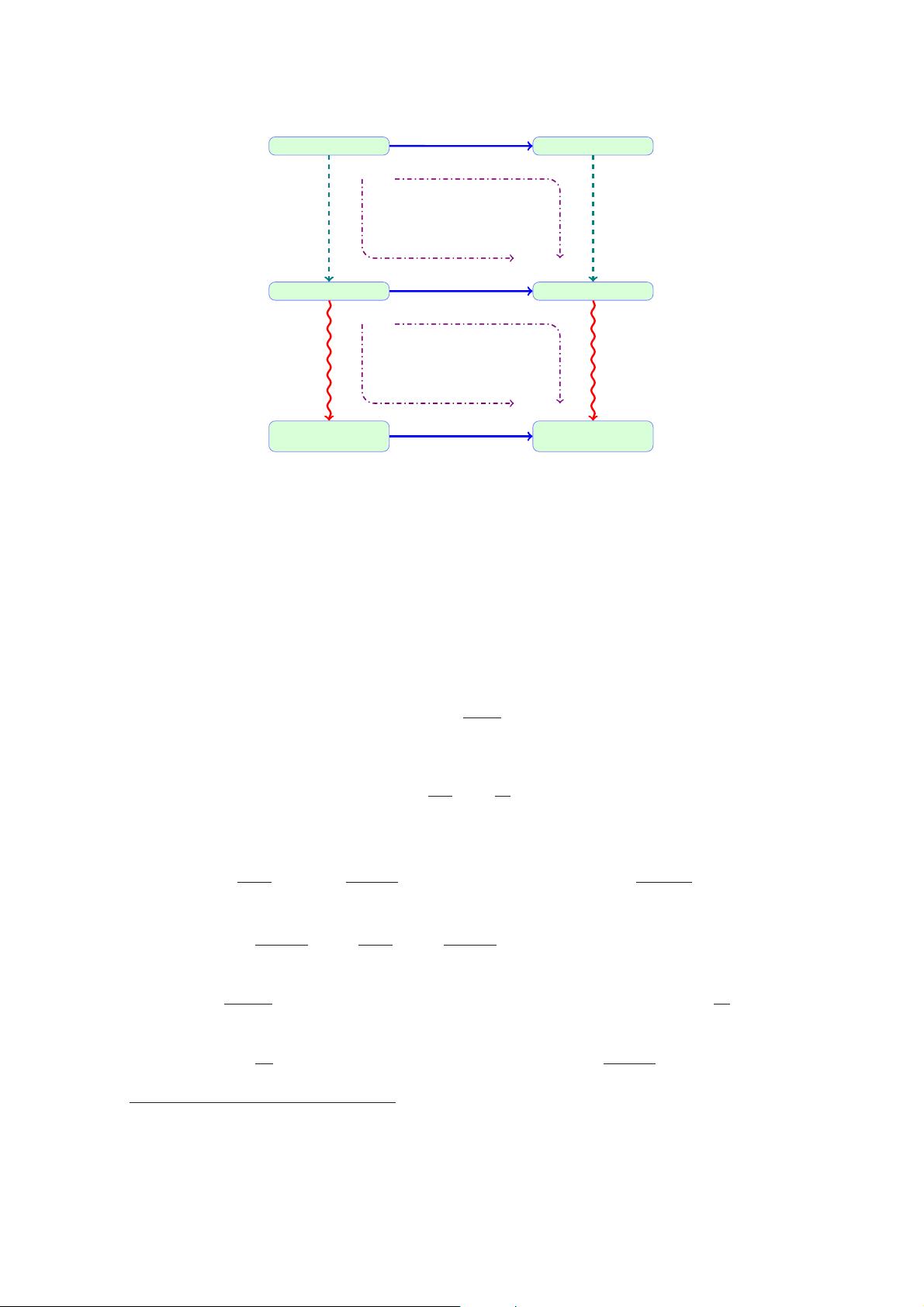
amining both of these limits in diﬀerent order s , as illustrated in ﬁgure

1, we will show

that by following both paths one can gener at e a single new geometry, which is the EVH

ultraspinning KAdS (EVH-US-KAdS) black hole in odd dimensions.

Moreover, as it is shown in the lower part of ﬁgure

1, we investigate not only EVH

and US limits commute with each other, but also the near hori zon of EVH-US-KAdS black

hole can be obtained by performing an appropriate ultraspinning limit on the near h ori z on

of the EVH-K AdS solution. We also explore the existence of a dual CFT by following

EVH/CFT to ﬁnd a low energy description for EVH at large angular momentum.

This paper is organized as follows. In section

2 we review the general KAdS black

hole, followed by its US and (N)EVH limits as well as the near horizon of (N)EVH cases.

In section

3 we show that US-KAdS has an EVH conﬁguration, that can be reproduced by

applying ultraspinning limit on EVH soluti on , and v i c e versa. In section

4 we present t he

near horizon geometr y of the obtained solutions by diﬀerent strategies. Furthermore, in

section

5 we discuss the thermodynamics of BTZ black hol e , which is located in the near

horizon geometry of our NEVH-US solutions in section

6. We also explore a super-entropic

EVH solution in section

6. The section 7 is devoted to conclusions with some remar k s. In

appendix

A we discuss on the topology of the obtained EVH-US sol ut i ons .

– 3 –

剩余30页未读，继续阅读

评论收藏

内容反馈

weixin_38727087

粉丝: 6
资源: 965

极速消失极限时消失的水平Kerr-AdS黑洞

极端消失的水平黑洞的近层结构

具有幻影标量场的AdS黑洞

近地平线极端Kerr-AdS-NUT几何的隐藏对称

Kerr-AdS黑洞的焦耳-汤姆森展开

三维广义相对论中的熵：Kerr-AdS黑洞

物质耦合的超对称Kerr-Newman-AdS4黑洞

Kerr-Newman-NUT-AdS黑洞的隐藏共形对称性

足够小的单旋转Kerr-AdS黑洞的热力学

Kerr–Newman-AdS黑洞在Rastall重力作用下被完美的流体物质包围

超熵黑洞与Kerr-CFT对应

Kerr-Schild复本和复杂的世界线

Kerr-AdS黑洞时空中的界面

极端Kerr-Taub-NUT黑洞近地平线区域的电磁辐射

Kerr黑洞时空中大规模标量场的拟束缚态：超越氢逼近

论文研究 - Kerr-Newman黑洞如何因If（Δ）问题而导致引力是否为量子的判据

Kerr-Newman-de Sitter黑洞的欧氏量化

论文研究 - 激光物理诱导的Kerr-Newman黑洞如何在不点燃黑洞炸弹的情况下释放引力波（实验室中迷你黑洞的爆炸）

Kerr-MOG黑洞的最内层圆形轨道

Kerr-Sen黑洞中带有旋转粒子的Penrose碰撞过程的最大效率

Kerr-Newman黑洞，带弦校正

带电加速AdS黑洞和全息热引擎的热力学

Kerr-de Sitter黑洞时空中任意旋量的费米隧穿辐射的精确修正

具有单个Killing矢量场的黑洞：黑色谐振器

具有标量场的Kerr-（anti-）de Sitter黑洞中的弱宇宙检查猜想

Kerr-Newman（A）dS黑洞的近层对称性和熵公式

AdS黑洞的行动增长

AdS braneworld黑洞的热力学几何形状和相变

Kerr-de Sitter黑洞的熵

最新资源