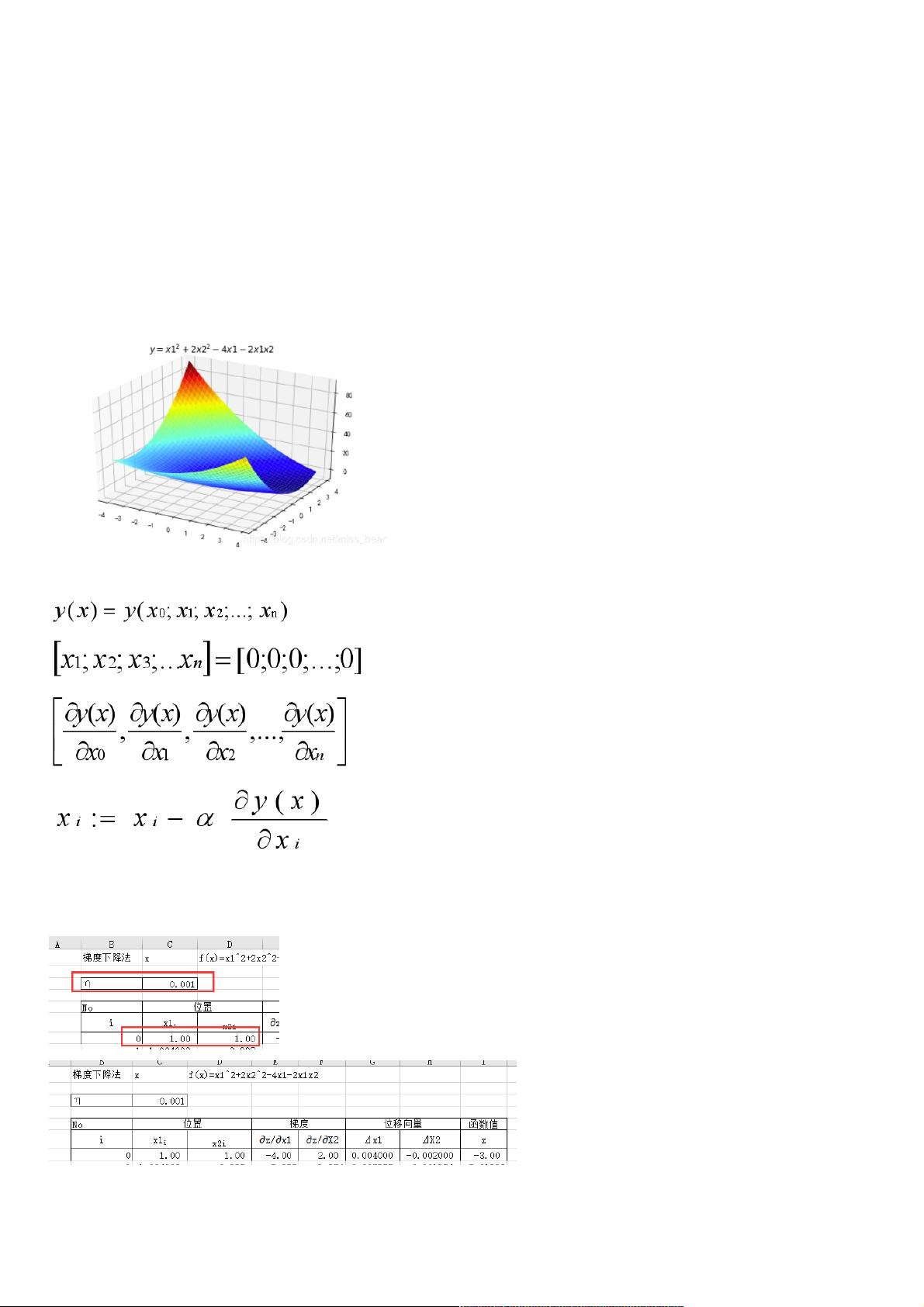
人工智能与机器学习-梯度下降法

人工智能与机器学习-梯度下降法 一、梯度下降法概述 梯度下降法（Gradient descent）是一个一阶最优化算法。 要使用梯度下降法找到一个函数的局部极小值，必须向函数上当前点对应梯度（或者是近似梯度）的反方向的规定步长距离点进行迭代搜索。 二、梯度下降法直观理解 以人下山为例，要到达最低点，需要以下步骤： 第一步，明确自己现在所处的位置 第二步，找到相对于该位置而言下降最快的方向 第三步，沿着第二步找到的方向走一小步，然后到底一个新的位置，这时候的位置就比原来更低 第四步，又明确当前所处位置，即回到第一步 第五步，到底最低点后就停下 基于以上步骤，就能够找到最低点，以下图为例 三、多 《人工智能与机器学习-梯度下降法》 梯度下降法是机器学习和人工智能领域中一个基础且重要的优化算法，尤其在训练模型时用于寻找损失函数的最小值。它是一种一阶最优化方法，通过沿着目标函数梯度的负方向进行迭代更新，逐步接近局部最优解。 一、梯度下降法概述 梯度下降法的基本思想是：在每次迭代中，我们计算当前点的梯度，然后朝着梯度的反方向移动一定的步长（学习率），以期望在后续的迭代中使目标函数的值不断减小。这个过程会一直持续，直到达到局部最小值或者满足停止条件，如迭代次数限制或函数值变化足够小。 二、梯度下降法直观理解 用下山的比喻来解释梯度下降法，我们可以想象自己站在一座山的山顶，想要找到通往山谷的最快路径。我们需要知道当前所在位置；找到当前位置下坡最快的方向，即当前位置的梯度方向；然后，沿着这个方向迈一小步，到达新的位置，这个位置比之前更低；接着，再次确定新位置，重复这个过程，直至抵达山谷底部，即函数的局部最小值。 三、多元函数的梯度下降解法 对于多元函数，梯度下降法需要计算目标函数关于每个自变量的偏导数，形成梯度向量。初始点的选择通常是随机的，然后按照各个自变量的偏导数与学习率的乘积更新各自变量的值。迭代公式如下： \[ x_i^{(k+1)} = x_i^{(k)} - \alpha \frac{\partial f}{\partial x_i} \] 其中，\( \alpha \) 是学习率，\( k \) 表示当前迭代次数，\( x_i \) 是第 \( i \) 个自变量。 四、实例 1. Python与Excel实现 在Python中，我们可以利用numpy库计算梯度，matplotlib库绘制函数图像，通过循环迭代实现梯度下降法。Excel同样可以实现这一过程，但通常较为繁琐，需要手动计算每个步骤的梯度和更新值。Python的优势在于可以方便地进行大量计算和自动化处理，而Excel则适用于小型问题的解决和可视化。 2. Python计算极小值与极小点并画出图像 Python代码示例中，我们定义了目标函数，计算了其偏导数，并使用梯度下降法进行迭代求解。同时，还绘制了三维图像来展示函数的表面形态，以便更好地理解梯度下降的过程。 总结来说，梯度下降法在人工智能和机器学习中发挥着核心作用，尤其是在深度学习中，用于训练神经网络模型的权重和偏置参数。尽管有多种优化算法，如随机梯度下降（SGD）、动量法等，但梯度下降法作为基础算法，理解其原理和应用至关重要。