没有合适的资源?快使用搜索试试~ 我知道了~
温馨提示
This article addresses the autonomy of joint radio resource management (JRRM) between heterogeneous radio access technologies (RATs) owned by multiple operators. By modeling the inter-operator competition as a general-sum Markov game, correlated-Q learnin
资源推荐
资源详情
资源评论

THE JOURNAL OF CHINA UNIVERSITIES OF POSTS AND TELECOMMUNICATIONS
Volume 14, Issue 3, September 2007
ZHANG Yong-jing, LIN Yue-wei
Markov game for autonomic joint radio resource
management in a multi-operator scenario
CLC number TN929.5 Document A Article ID 1005-8885 (2007) 03-0048-08
Abstract This article addresses the autonomy of joint radio
resource management (JRRM) between heterogeneous radio
access technologies (RATs) owned by multiple operators. By
modeling the inter-operator competition as a general-sum
Markov game, correlated-Q learning (CE-Q) is introduced to
generate the operators’ pricing and admission policies at the
correlated equilibrium autonomically. The heterogeneity in
terms of coverage, service suitability, and cell capacity amongst
different RATs are considered in the input state space, which is
generalized using multi-layer feed-forward neural networks for
less memory requirement. Simulation results indicate that the
proposed algorithm can produce rational JRRM polices for each
network under different load conditions through the autonomic
learning process. Such policies guide the traffic toward an
optimized distribution and improved resource utilization, which
results in the highest network profits and lowest blocking
probability compared to other self-learning algorithms.
Keywords autonomic, JRRM, multi-operator, reinforcement
learning (RL), Markov game
1 Introduction
The co-existence of heterogeneous RATs, including universal
mobile telecommunications system (UMTS), wireless local
area networks (WLAN), and many others, characterizes the
Beyond 3rd generation (B3G) environment in the future. The
overlapping coverage, diverse service requirements,
complementary technical characteristics entail the integration
and cooperation between the RATs for better user experience
and higher system performance [1]. Based on the software-
defined radio technology, the end-to-end reconfigu- rability [2]
has been developed to facilitate the JRRM by providing
terminals and networks the abilities of dynamically selecting
and adapting to the required RATs and operating spectrum
range [3]. Several studies have been done in this area concerning
Received date: 2006-03-03
ZHANG Yong-jing ( ), LIN Yue-wei
School of Telecommunication Engineering, Beijing University of Posts and
Telecommunications, Beijing 100876, China
E-mail: yongjing.zhang@gmail.com
different aspects, such as joint session admission control [4],
joint session scheduling [5], and joint load control [6]. However,
they focus mostly on the single-operator scenario where a
centralized JRRM controller can have the resources well
managed across RATs in a cooperative way. In a
multi-operator scenario, such entity is hardly applicable so
that JRRM tasks should be decentralized and the
inter-operator competition must also be considered.
Furthermore, existing studied have not addressed the
autonomy of the management, which is becoming more and
more important as the system complexity grows higher with
the increasing technologies and devices that overwhelm users
and network administrators [7].
To generate the optimal JRRM policies for individual RAT
autonomically, learning capability is indispensable to the
JRRM entities (called agents). Amongst several categories of
machine learning techniques, RL seems most promising for its
successful applications in many areas including robotics,
computer game playing [8], as well as, mobile communication
systems [9]. RL enables an agent to learn to act without
knowing the environment model; however, its convergence
requires the assumption of Markov decision process (MDP),
which is no longer satisfied in a multi-agent environment as in
the multi-operator JRRM issue. Fortunately, several multi-
agent RL (MARL) algorithms [1013] have been developed in
the framework of Markov game. In spite of their respective
limitations, these algorithms provide the opportunities for the
solution to the problem.
In this article, an attempt is made to realize the multi-
operator JRRM in an autonomic way by formulating it as a
Markov game and using the CE-Q approach [13]. Considering
the practical challenge of the memory requirement, neural
network-based function approximation is also adopted in the
solution to generalize the large input state space.
2 Problem definition
2.1 JRRM in a multi-operator scenario
Supposing multiple operators running several heterogeneous
RATs overlapped in a densely populated area, people equipped
No. 3 ZHANG Yong-jing, et al.: Markov game for autonomic joint radio resource management… 49
with multi-mode or reconfigurable terminals can enjoy their
wireless applications via buying the access services provided
by any RAT. Although the co-existing RATs could have
diverse coverage, capacities, and technical specialties, they
may be suitable for different types of service from the
perspective of resource utilization. For example, UMTS is
more efficient to provide real-time (RT) services (e.g. voice)
with high mobility support, while WLAN is more economic in
transmitting non-real-time (NRT) services (e.g. file transferring)
within limited area. In other words, it would cost the RATs
unequally to provide the same level of quality of service (QoS)
for a certain type of service. Therefore, how to allocate the
limited resources efficiently to the most suitable services to
produce the highest profits becomes the issue of concern to
the operators.
One practice is to adjust the policy of service provisioning
on different services and network conditions. Specifically,
JRRM agents can offer high QoS with low price to encourage
user’s access to the desirable service when the network is
lightly loaded, and do the opposite in the reverse situation.
Such policies are delivered to the end users (or the intelligent
agents on their terminals) via certain logical control channel
(e.g. a RAT-specific broadcast channel or the cognitive pilot
channe [14], which is out of the scope of this study). Then
users can make their best choices amongst these offers to
maximize their utilities. Hopefully, in this way, traffic can be
directed to a reasonable distribution to realize the optimized
JRRM.
Despite the technical complementarities between the
co-existing RATs, inter-operator competition is still
non-negligible in a multi-operator scenario. For instance, a
UMTS network may compete with WLAN for NRT services if
its capacity permits. Thus the distributed policies in different
RATs may conflict with each other so that the executing
results would be unforeseeable and undesirable. Meanwhile,
as the number of base stations (BS) or access points (AP)
grows with more and more novel RATs and micro-coverage
cells for richer service provisioning and higher system
capacity, the operation and administration complexity also
grows considerably. It is most desirable that the JRRM
policies amongst the RATs are self-managed to adapt to the
varying traffic demand without much human-intervened
planning and maintaining cost. These two considerations put
forward the challenge of how to generate autonomic and
effective policies for an intelligent JRRM agent in the light of
other agents’ moves. An option to the MARL in the Markov
game framework is as follows.
2.2 MARL
A standard RL problem can be modeled as a tuple of MDP
<S, A, R, T>, where S={s
1
, s
2
,…, s
n
} is the possible state space
of the environment, A={a
1
, a
2
,…,a
m
} is the possible action
space of the agent, R: S × A → is the reward function of the
agent, and T: S × A → P
d
(S) is the state transition function,
where P
d
(S) denotes the set of probability distributions over S.
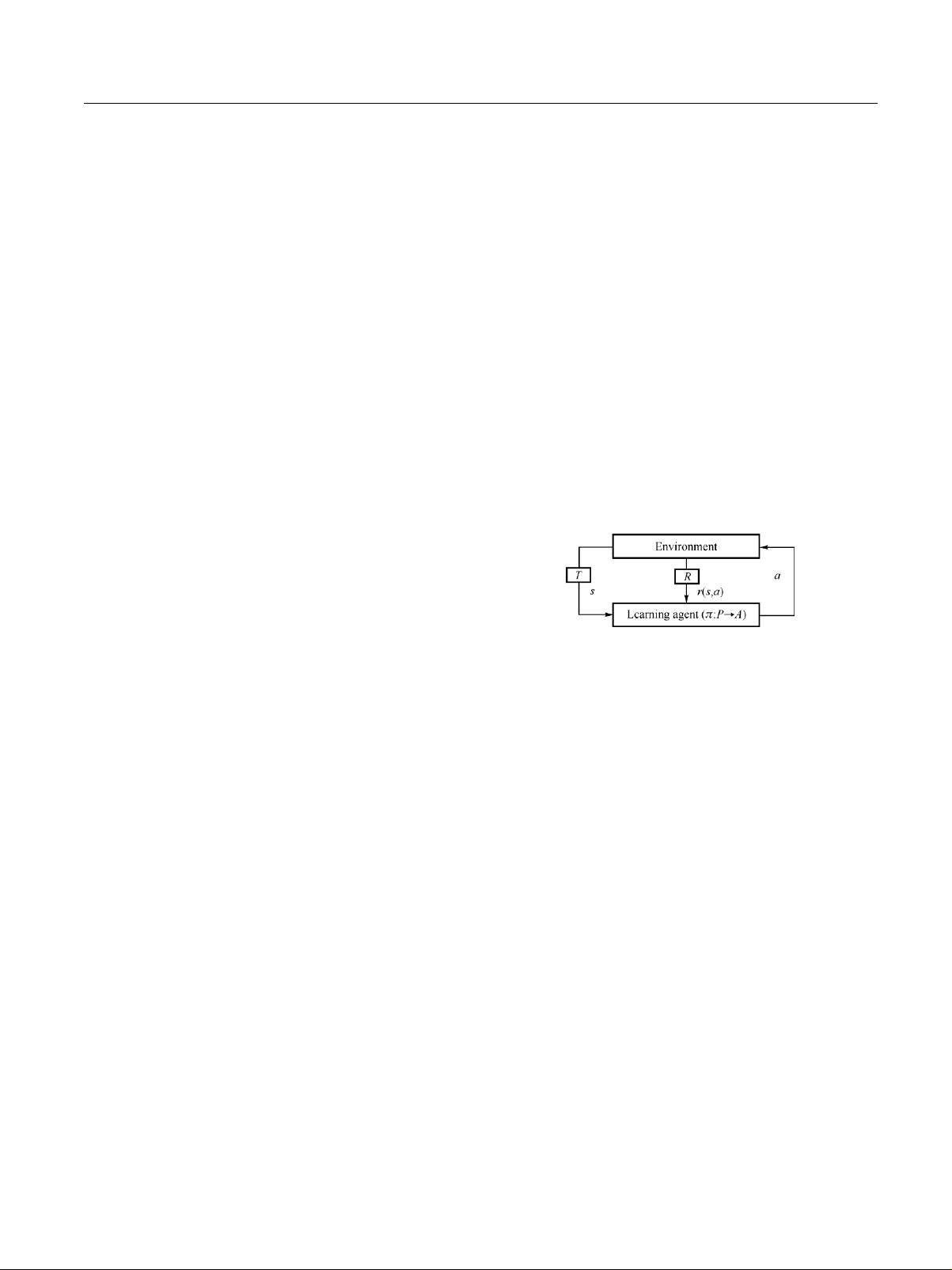
A basic RL model is illustrated in Fig. 1. The agent
perceives the state
sS
of the environment and decides the
action
aA
following its current policy
S→A. Consequently,
the environment may change to a state
sS
according to T
and the agent receives a scalar reinforcement signal r(s, a),
called the immediate reward, according to R. Then the agent
revises its policy using
s
and r(s, a). Such a process
continues in a iterative way and the final goal is to find the
optimal policy
*( )sS
that maximizes the agent’s
expected long-term reward (or the value) in each state:
0
0
( ) ( , ( )) |
t
tt
t
V s E r s s s s
(1)
where,
(0, 1)
is the discount factor reflecting the
significance of the future reward relative to the current one.
Fig. 1 The standard RL model
Single-agent RL has been well studied during the past
decades. One of the most popular algorithms is Q-learning [15],
which is an off-policy model-free approach. It associates a
Q-value with each pair of state-action (s, a) and learns the
optimal policy through the simple value-iteration rule:
1
( , ) (1 ) ( , ) ( ( ))
t t t
Q s a Q s a r V s
(2)
( ) max ( , )
t
aA
V s Q s a
(3)
where,
[0,1)
is the learning rate. As t → ∞, if the learning
rate is decreased suitably to 0 and the Q-value of each (s, a)
pair is visited infinitely often, Q
t
(s, a) converges to the optimal
value Q
*
(s, a) with probability 1 [15]. Then, the optimal policy
is obtained as
**
( ) argmax ( , )
a
s Q s a
(4)
In a multi-agent context, the state transition T is no longer
guaranteed to be Markovian from a single agent’s point of
view, because its environment is affected by other agents’
actions. Thus the direct application of traditional RL algorithms
(e.g. Q-learning) in a multi-agent environment could be
problematic. By extending each state of a MDP as a matrix
game between agents, a Markov game framework has been
developed for MARL and a handful of algorithms [1013] are
now available based on the Q-learning principle. The common
剩余7页未读,继续阅读
资源评论

weixin_38723527
- 粉丝: 3
- 资源: 953
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功